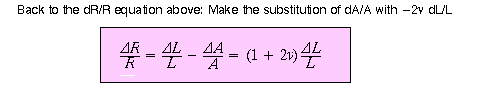
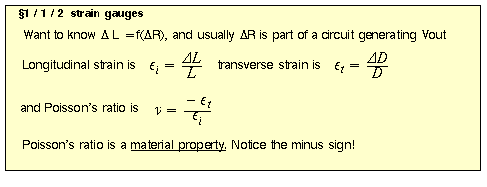
If Poisson's ratio is 0.5, the gauge factor is 1+1=2. If there is no piezoelectric effect, then knowing the gauge factor means you can figure out length change from resistance change. What is L in that context?

Finding Poisson's ratio. If a material maintains constant volume during stretching, what should n be? Say we're dealing with a rectanguloid of material of length l and side s. take differentials and set dV = 0 - no change in volume.














now what? remember that strain is dl/l !!



Therefore a 0.5 Poisson ratio is for completely incompressible material, like a metal. So typical gauge factor should be 2. Plexiglas it turns out has a Poisson ratio of 0.45. No material has a ratio greater than 0.5.

The gauge factor for constantin and nickel chromium alloy is 2, as you may expect.

Work out what the Poisson ratio is for a 1x1x1 cube stretched-without necking down-to a length of 2...
V=l x s2=1, so when l=2, s drops to 1/sqrt(2) = .707, resulting in a ratio of about 0.3...

Strain gauge amplifier: see yellow box strain gauge amplifier box, up in the lab, may remember it from EN3, or EN31.

Piezoelectric materials: charge displacement q = K*f where the stress on the material. and a nonzero rate of change of rho with strain.

Strain gauges and temperature: self heating; heat from the source the gauge is on.

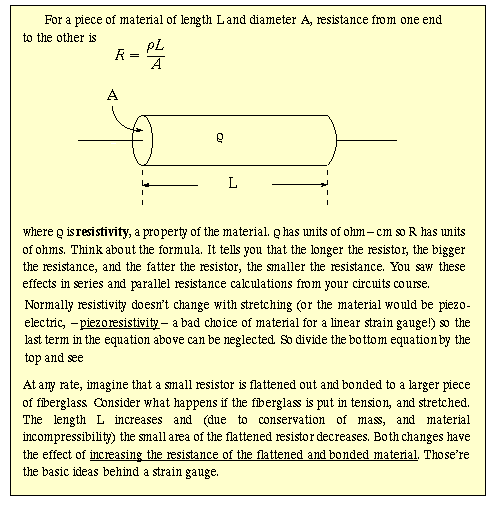
The bonded foil strain gauge is one of the most important transducers in the realm of engineering. The strain gauge metal is attached firmly to a strong flexible insulating transparent sheet. That sheet in turn is bonded by epoxy to the material whose strain should be measured.

A strain gauge is often formed in the serpentine shape shown below. [In the BLH strain gauges for the EN123 Lab, sometimes the thin foil is nickel chromium alloy.] Along the axis shown by the arrows a change in L by length DL results in a 14*DL change in total length of the strain gauge!

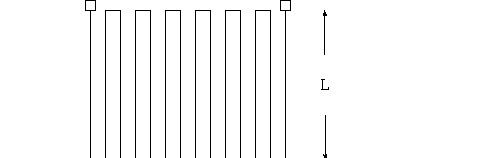
Look closely at one of the strain gauges and see if the pattern shown above is evident. You might see two strain gauges together, in a "rosette" pattern.

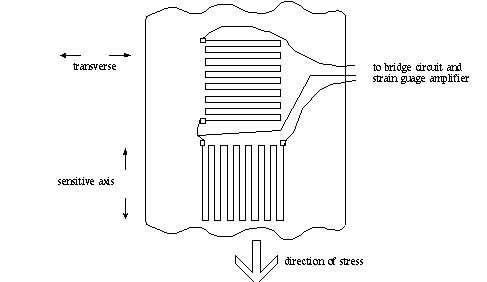
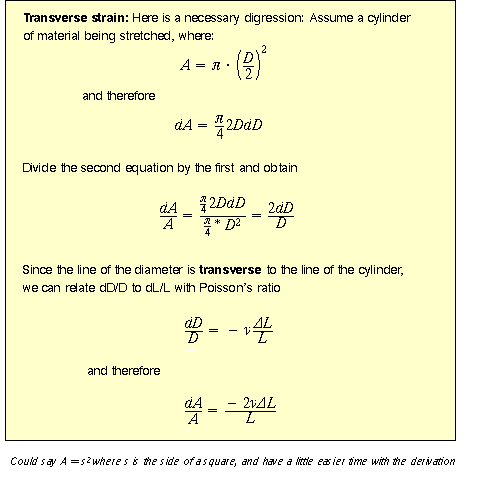
As the bar is stretched the transverse dimension decreases. (The cross section diminishes slightly; stretch a rubber band and watch it get thinner.)
The ratio

;


The change in transverse-oriented strain gauge resistance is


The strain gauge amplifier is set up to take account of both axial and transverse responses, so that the effective gauge factor for the measurement is


For the metal material used in our gauges, KS = 2.0

Another important reason for using rosette pairs of strain gauges is compensation for temperature effects. The amplifier is really using the ratio of resistance changes; to the extent that self heating or other common temperature effects change both resistances, a ratio of the changes will remain constant. This technique is particularly valuable on materials, like fiberglas, with low thermal conductivity. The effect of the rosette pattern is effectively to double the gauge factor to

Each individual SG has an unloaded resistance of either 120W or 350W, by convention.

�1 / 2 Calculation for microstrain amplifier

and if the gauge factor is properly used with the strain gauge amplifier, it basically tells you you can find what strain e is directly
(in microstrain, x 10-6). (See additional sheets.) For R=350 and Vp = 15 volts, I get a gain of 7000 or so for reading out directly in microstrain...I used the approx that


where, as shown below, R+DR is the resistance of a strain gauge in the lower leg of one side of a bridge and the voltage divider output of that leg is


Why is the beta approximation true? We show below, using Taylor series expansion:



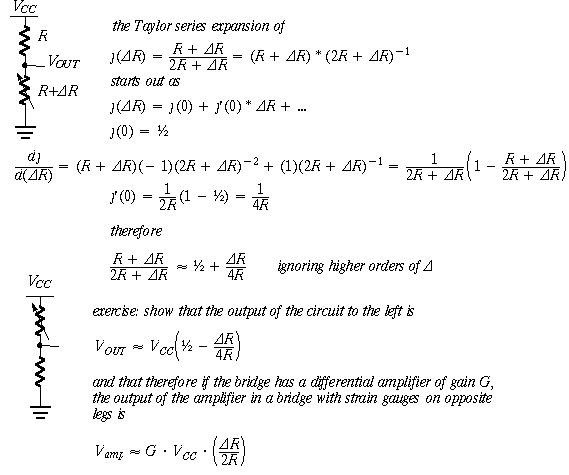
try it: if R = 120 and delR = 1, then (120+1)/(240+1) = .5021, and .0021 is 1/4 of 1/120...
see Thomas, Calculus and Analytic Geometry, page 785 ff

see matlab file sg123.m for calculations based on formula.  

�1 / 3 More than one active strain gauge in the bridge

An active strain gauge is one on the material being stressed. There may be other strain gauges in the bridge, there to be precision resistors.




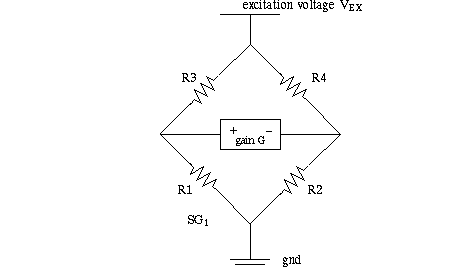
If there is one active strain gauge at position R1 then VOUT = VEX*G*DR/4R;
Now consider compression-tension vs bending.
comp bending
R1 & R2 on opposite sides CMRR VEX*G*DR/2R
R1 & R3 on opposite sides CMRR VEX*G*DR/2R
R1 & R4 on opposite sides VEX*G*DR/2R CMRR

Remember that longitudinal and transverse strain are related by Poisson's ratio. You should be able to work out when transverse strain gauges help compression or bending. For example, if there are longitudinal and transverse gauges on the same side, then they should be at R1, R4 to sense compression.

�1 / 4 Constant current for bridge excitation

See HP Guide to Strain Gauges, page 14.

�1 / 5 Bonding of strain gauge to material

Want high fidelity of strain gauge to material deformation
Adhesive: want to minimize the effect it has on SD deformation
Can use a thin layer of adhesive: that means cyanacrylate, that bonds 
one molecule thick. "Superglue" may be susceptible to chemical 
attack, such as acetone. In addition, cyanacrylate may be less stable 
than epoxy, a more chemically inert alternative. Epoxy is good for 
bonding to wood. 
Notice there's an up and a down side the each SG! 
What about the wires that lead away from the strain gauge? They may 
need to be strain-relieved. 

�1 / 6 Noise and grounding problems in strain gauges

Consider placing the strain gauge "foil" on a metal base with cyanacrylate. There will be capacitive coupling, significant because of the small d in the eA/d = C formula.
There may be leakage to the metal base ground (conductive coupling) through the plastic foil.

�1 / 7 Speed of response

May want to measure vibration (and we will, in Lab 3). At what frequency can metal vibrate? no more than 1000 Hz... What limits speed of response of the strain gauge? Capacitive coupling may be one thing.

�1 / 8 Temperature compensation

Use strain gauges for all 4 resistors in a bridge! Then any temperature change in the experiment will be completely compensated for. Except that the material under study may change also, due to temperature...but that may be part of the experiment, to study expansion due to temperature. Can't invoke Hooke's Law in that case.

Also may need to worry about resistance changes due to self heating. V2/R for 10 volts and 120 ohms is nearly a watt! A SG bonded with epoxy may be less able to dissipate heat than its partners in the bridge.

Summary List
* types of position measuring devices: example of VR exoskeleton problem
* definition of resistivity; definition of strain
* Poisson's ratio for incompressible material
* Strain gauge in a bridge circuit
Taylor Series approximation
* Temperature effects on SGs and the underlying material
*

Application of length sensors: how to sense hand and finger position 
in a virtual reality glove.optical sensors in fingers? find a 
website! Compare muscle spindles to strain gauges. 

1988: Volume 2 Berkeley Physics page 128, CONDUCTIVITY graph