Matrix Finite Element Methods By Energy Minimization

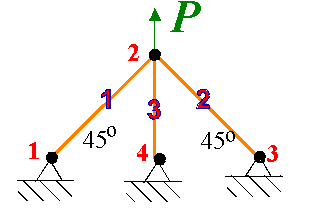
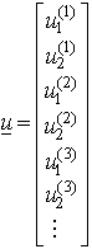
· Write Potential Energy as a function of nodal displacements: V=V(u)

· Minimize V(u):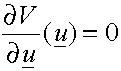

· Solve for u

To calculate V(u):

Write the strain and axial force of each member as a function of nodal displacements.

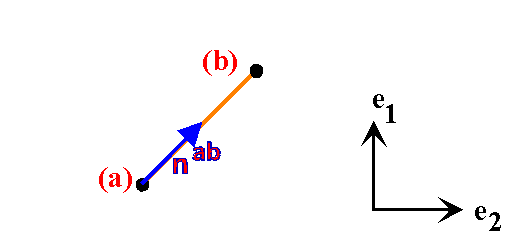
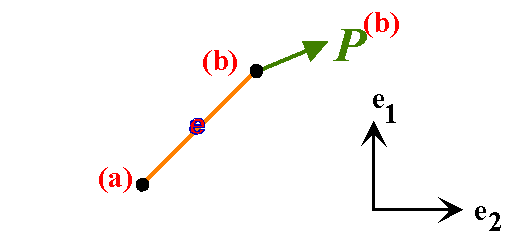
For Element e connected to joints (a) and (b):

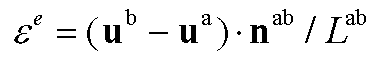
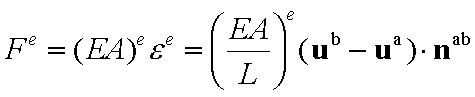
Write the Strain Energy for each member:

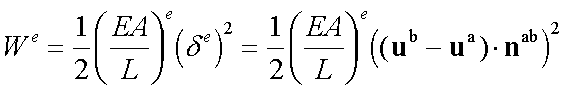
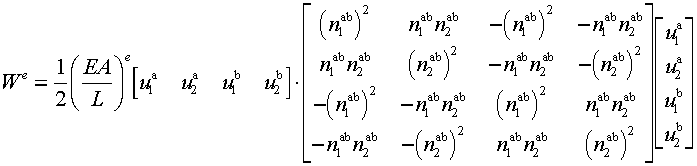
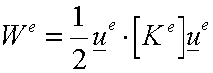
and are the element stiffness matrix and element displacement vector. is symmetric!!!

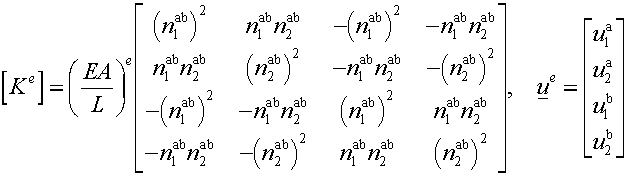
In 3D

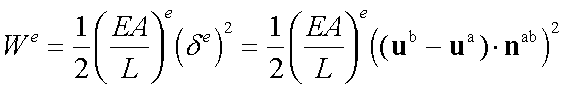
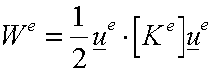
(Same as it ever was…)

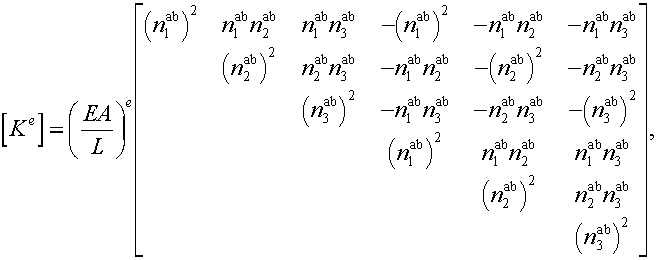
The Global Stiffness Matrix

The total strain energy of the truss may be computed by adding together the strain energy of each element:

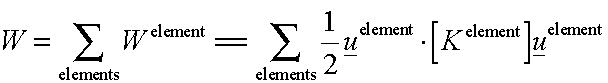
It is more convenient to express W in terms of the global displacement vector, u

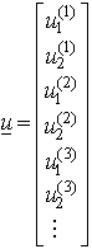
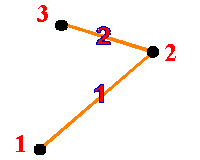
Consider a Two-Member (Two-Dimensional) Truss:

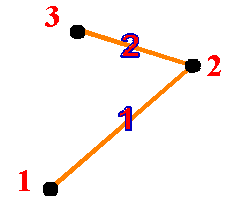
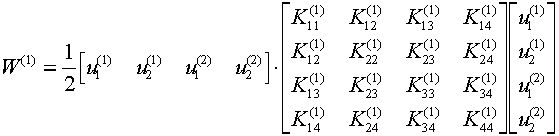
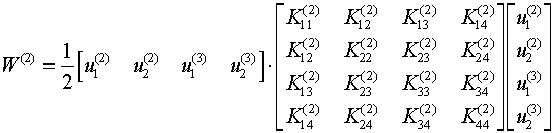
W⁽¹⁾ and W⁽²⁾ in terms of the global displacement vector u:

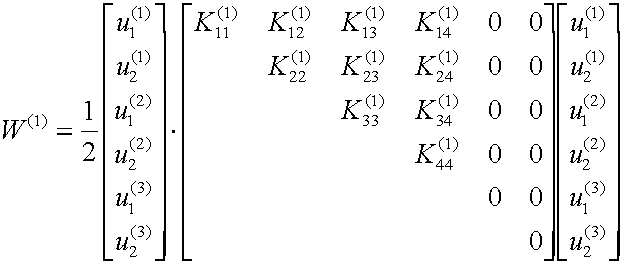
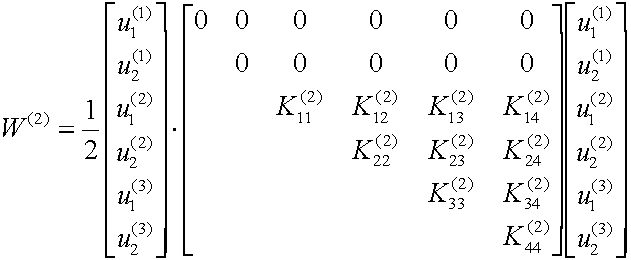
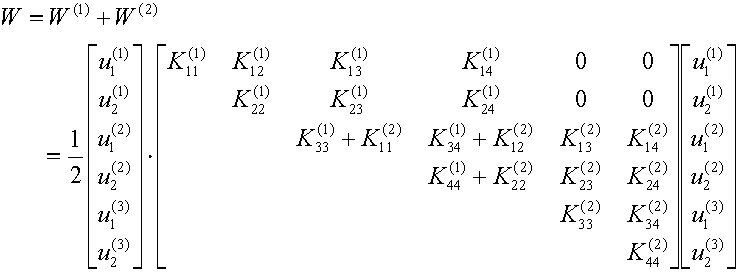
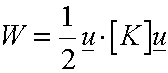
[K] is the Global Stiffness Matrix. It is the sum of all the element stiffness matrices.

Because the element stiffness matrix is symmetric, the global stiffness matrix must also be symmetric.

CAUTION:

SOME ASSEMBLY REQUIRED!!!

(Batteries not included)

Bookkeeping:

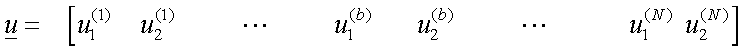The displacement of node #b in the e_i-direction, u_i^(b) (i=1,2) is the (2(b-1)+i)^th element of the global displacement vector, u:

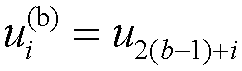
The degree of freedom number assigned to the displacement of node b in the i-direction is (2(b-1)+i).

In 3D: 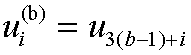and the degree of freedom number assigned to the displacement of node b in the i-direction is (3(b-1)+i).)

The global stiffness positioning (2D):

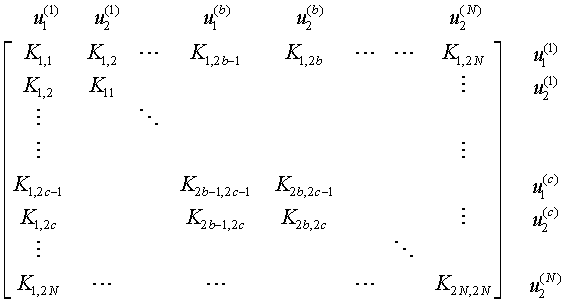
Where do the element stiffness components land?

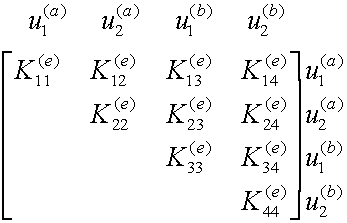
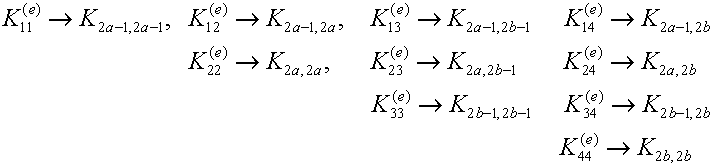
Externally Applied Forces

These are specified by prescribing the node on which the loading acts and the force vector P.

Potential energy due this load is then

The total contribution to the potential energy due to prescribed forces on all of the loaded nodes is

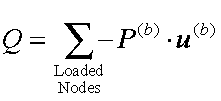
Global residual force vector: r

But of course, we have to write Q in terms of the global force vector u.

Q=-r×u

ASSEMBLY REQUIRED!!!

Recall the degree of freedom number assigned to the displacement of node b in the i-direction is (2(b-1)+i).

3D degree of freedom number assigned to the displacement of node b in the i-direction is (3(b-1)+i).

Stay Tuned!!

Still to Come:

· Minimize V[u]

· Take boundary conditions into account

· Solve for u.

· Go back to get element forces and strains.