Chapter 12
Dynamic solutions for elastic solids
In
this section we discuss briefly the motion
of elastic solids subjected to some loading.
We will consider two topics: (1) wave propagation in an elastic solid;
and (2) vibrations.
12.1 Wave
propagation in a string
We
can develop some physical intuition into how deformable solids will move by
solving some simple problems. We start
by analyzing motion of strings these are simple but it turns out that waves in a string behave
the same way as plane waves in an elastic solid.
Example 1: Traveling wave propagation in
a stretched string with given initial conditions
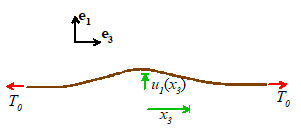 We can learn a lot about the behavior of waves in
solids by looking at the behavior of a stretched string. For this purpose we
solve the following problem: An infinitely
long string under axial tension as at rest and has a transverse displacement
We can learn a lot about the behavior of waves in
solids by looking at the behavior of a stretched string. For this purpose we
solve the following problem: An infinitely
long string under axial tension as at rest and has a transverse displacement
at time t=0.
Find the subsequent motion of the string.
We derived the governing equation
for a string in Chapter 10. It is
where is the wave speed.
This
is the famous wave equation. It has a
rather simple general solution where f and
g are arbitrary functions, which must
be determined from the initial conditions (and if the string has ends, boundary
conditions at the ends). For the
current case the initial conditions for give
where
. To
solve these for f and g just integrate the second one, which
gives us two equations
where A is a constant. Solve
these
So the solution is
The solution (with initial
condition ) is
animated in the figure below

You
can see the initial disturbance split into two waves, which propagate at stead
speed down the string. These are the
functions f and g: f is a wave propagating to
the right, and g is a wave
propagating to the left. Of course, the wave
motion is just an illusion every point in the string moves transverse to
its axis, but like the ‘wave’ in an athletic stadium the disturbance appears to
propagate even though the crowd are just raising and lowering their arms.
Example 2: Traveling wave propagation in
a stretched string with prescribed motion at an end
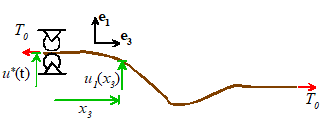 The same general solution can be used to solve any
traveling wave problem. For example,
suppose we hold one end of a very long string.
The string is at rest with everywhere at t=0. We then move the end we
are holding with a prescribed displacement . Find
the displacement.
The same general solution can be used to solve any
traveling wave problem. For example,
suppose we hold one end of a very long string.
The string is at rest with everywhere at t=0. We then move the end we
are holding with a prescribed displacement . Find
the displacement.
As
before, the solution is . Note that must be calculated for all ,
since for any its argument will be negative for sufficiently
large t, but need only be defined for , since its argument is never negative
.The initial conditions give
Integrate the second
equation and then solve for f and,g to see that
This gives us g everywhere we need it, and tells us for . We
can find for from the boundary condition on displacement at
We
already know so it follows that
.
We
now have the complete solution, which can be re-written as
It
is a bit easier to visualize this if we re-write the conditional as
This
equation says that every point on the string experiences the same history of
displacement , but a point at position will experience the displacement at a time later than the point at . Of
course we already know that, but it is nice to see the math work out.
The
figure below animates the behavior of a string that has its leftmost end moved
through two cycles of a sin wave.

 Example 3:
Reflections at a boundary
Example 3:
Reflections at a boundary
Finally, we look at what
happens when a wave reaches the end of a string. The figure shows the two possible types of
boundary: at is a fixed end; is a free end. The string is at rest at time t=0 and
has a transverse displacement
For simplicity we assume that the string is only displaced
near the origin, and in particular at .
The two boundary conditions at the ends are
We
can satisfy these by extending the string to , and introducing initial displacements into
the imaginary parts of the string outside that will satisfy the two boundary
conditions. Hopefully you can see that
to cancel the forward propagating wave (to keep the end fixed at ) you need to introduce an initial displacement
in the opposite direction centered at , while to keep the slope fixed at , you need to introduce a disturbance of the
same sign at . The figure below illustrates the idea
graphically: the waves generated by the initial displacements of the fictitious
blue parts of the string will reach the boundaries at just the same time as
those in the real, brown parts: on the right, the waves cancel and give zero
displacement; on the left, they combine and keep the slope zero.
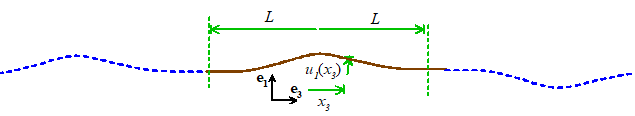
Of
course the process does not end here: we need to continue extending the string
to both left and right and add the appropriate initial displacements to satisfy
boundary conditions at the two ends for all time. The animation below shows the full sequence
(the left end is free; the right end is fixed).
If you enjoy puzzles and some basic matlab coding you might find it
instructive to try to reproduce the result yourself.

You can watch the two ends
to understand the two types of reflection:
·
At a fixed end, a
wave with positive deflection reflects as one with a negative deflection;
·
At a free end, a
wave with positive deflection reflects as one with a positive deflection sign.
It is helpful to understand
how reflections influence transverse forces in the string as well. Recall
that the transverse force in a string is related to the deflection by
An animation of the
transverse force is shown below

Watch the animation and convince yourself that
·
At a fixed end, a
positive transverse force is reflected as a positive transverse force;
·
At a free end, a
positive transverse force is reflected as a negative transverse force.
The rules governing
reflections of forces are the opposite to those governing displacement.
12.2:
Pressure and shear plane waves in 3D elastic solids
Now
that we understand strings, we can think about waves in 3D elastic solids. Start with the special case of an infinitely
large, isotropic linear elastic solid with Young’s modulus E, Poissons ratio and mass density that fills all of space. Consider motion of the form
This
describes a so-called ‘plane wave’ that propagates in the direction.
To visualize the motion note that
(1)
every point that
lies in a particular plane has the same displacement
(2)
is a displacement transverse to the
propagation direction (a so called ‘Shear wave’ or S-wave). This is just like the motion of a wave moving
along a string.
(3)
it is a displacement parallel to the wave
propagation direction (a ‘Pressure wave’ or P-wave). This type of motion can’t occur in a string,
but it does occur in long flexible springs (like a slinky) which can be
stretched axially.
We
can now substitute this displacement field into the elasticity equations:
 The strain-displacement relation gives
The strain-displacement relation gives
 The elastic stress-strain law gives
The elastic stress-strain law gives
 Finally, the linear momentum balance equation
gives
Finally, the linear momentum balance equation
gives
where
 is the speed of longitudinal wave propagation
through the solid
is the speed of longitudinal wave propagation
through the solid
 is the speed of shear wave propagation through
the solid.
is the speed of shear wave propagation through
the solid.
The
longitudinal wave is always faster than the shear wave.
These
are the same wave equation that governs the motion of a string. Everything we learned about strings applies
without modification to plane waves in 3D elastic solids.
Example 1: An isotropic, linear elastic half space with Young’s
modulus E, Poisson’s ratio and mass density occupies the region . The
solid is at rest and stress free at time t=0. For t>0 it is subjected to a
pressure p(t) on as shown in the picture.
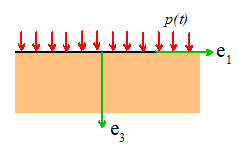
Solution: The displacement and stress fields in the solid (as a
function of time and position) are
where
is the speed of longitudinal wave propagation
through the solid. All other
displacement and stress components are zero.
For the particular case of a constant (i.e. time independent) pressure,
magnitude ,
applied to the surface
Evidently,
a stress pulse equal in magnitude to the surface pressure propagates vertically
through the half-space with speed .
Notice
that the velocity of the solid is constant in the region ,
and the velocity is related to the pressure by
Derivation: The
solution can be derived as follows.
1.
The solution to
the 1-D wave equation is
where f and g are two functions that
must be chosen to satisfy boundary and initial conditions.
2. The initial conditions are
where the prime denotes differentiation with respect
to its argument. Solving these equations
shows that
where
A is some constant.
3. Observe that for t>0, so that . Substituting this result back into the
solution in (4) gives .
4. Next, use the
boundary condition at to see that
where
B is a constant of integration.
5.
Finally, B can be determined by setting t=0 in the result of (7) and recalling
from step (5) that . This shows that B=-A and so
as
stated.
Example 2: Surface
subjected to time varying shear traction
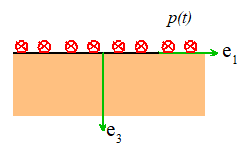
An
isotropic, linear elastic half space with Youngs modulus E and Poisson’s ratio and mass density occupies the region . The
solid is at rest and stress free at time t=0. For t>0 it is subjected to a
uniform anti-plane shear traction p(t) on . Calculate the displacement, stress and strain
fields in the solid.
It is straightforward to
show that in this case
where is the speed of shear waves propagating
through the solid. The details are left
as an exercise.
Example 3: 1-D Bar
subjected to end loading
 This solution is a cheat, because it doesn’t satisfy
the full 3D equations of elasticity, but it turns out to be quite accurate.
This solution is a cheat, because it doesn’t satisfy
the full 3D equations of elasticity, but it turns out to be quite accurate.
A
long thin rod occupying the region is made from a homogeneous, isotropic, linear
elastic material with Young’s modulus E and mass density . At time t<0 it is at rest and free
of stress. At time t=0 it is
subjected to a pressure p(t) at one end.
Calculate the displacement and stress fields in the solid.
We
cheat by modeling this as a 1-D problem.
We assume that is the only nonzero stress component, in which
case the constitutive law and balance of linear momentum require that
where
is the wave speed. This equation is exact for but cannot be correct in general, since
transverse motion is neglected. In
practice waves are repeatedly reflected off the sides of the bar, which behaves
as a wave-guide.
It is straightforward to solve the equation to
see that
Summary of Wave Speeds
in isotropic elastic solids.
It is worth summarizing the
three wave speeds calculated in the preceding sections. Recall that
It
is possible to show that, for all positive definite materials (those with
positive definite strain energy density a thermodynamic constraint) . For most real materials .
There
are also special kinds of waves (called Rayleigh and Stoneley waves) that
travel near the surface of a solid, or near the interface between two
dissimilar solids, respectively. These
waves have their own speeds. Rayleigh
waves are discussed in more detail in Section 11.3 below.
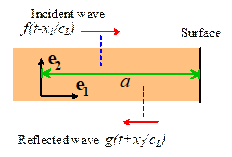 Reflection of waves traveling normal to a free surface
Reflection of waves traveling normal to a free surface
Suppose that a longitudinal
wave with stress state
is
incident on a free surface at . Calculate the state of stress in the solid as
a function of time, accounting for the stress free surface.
To
visualize the wave, imagine that it is a front, such as would be generated by
applying a constant uniform pressure at at time t=0. The material ahead of the front is at rest,
and stress free, while behind the front material has a constant stress and
velocity.
At
time the front would reach the free surface and be
reflected. Let the horizontal stress
associated with the reflected wave be
(we
need a + in the argument because the wave travels to the left and has negative
velocity). For the stress to vanish at the free surface, we must have
so,
and the full solution
consists of both incident and reflected waves
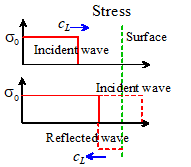
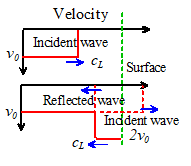
As a specific example,
consider a plane, constant-stress wave that is incident on a free surface. The
histories of stress and velocity in the solid are illustrated in the figures
above. In this case:
1. Behind the incident stress wave, the stress is
constant, with magnitude . The velocity of the solid is constant, and
related to the stress by
2. At time the stress wave reaches the free surface. At this time an equal and opposite stress
pulse is reflected from the free surface, and
propagates away from the surface.
3. Behind the reflected wave, the solid is stress free,
and, the solid has constant velocity
12.3 Rayleigh waves
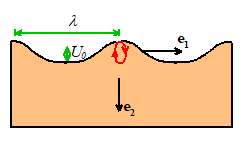
A
Rayleigh wave is a special type of wave which propagates near the surface of an
elastic solid. Assume that
 The solid
is an isotropic, linear elastic material with Young’s modulus ,
Poisson’s ratio and mass density
The solid
is an isotropic, linear elastic material with Young’s modulus ,
Poisson’s ratio and mass density
 The
solid has shear wave speed and longitudinal wave speed
The
solid has shear wave speed and longitudinal wave speed
 The
surface is free of tractions
The
surface is free of tractions
 A
Rayleigh wave with wavelength propagates in the direction
A
Rayleigh wave with wavelength propagates in the direction
The
nonzero components of displacement and stress in a Rayleigh wave are
where
,
is the amplitude of the vertical displacement
at the free surface, is the wavenumber; ,
;
and is the Rayleigh wave speed, which is the
positive real root of
This
equation can easily be solved for with a symbolic manipulation program, which
will most likely return 6 roots. The
root of interest lies in the range for .
The solution can be approximated by with an error of less than 0.6% over the full
range of Poisson ratio.
You
can use either the real or imaginary part of these expressions for the
displacement and stress fields (they are identical, except for a phase
difference). Of course, if you choose to take the real part of one of the
functions, you must take the real part for all the others as well. Note that
substituting in the expression for and setting yields the equation for the Rayleigh wave speed,
so the boundary condition is satisfied.
The variations with depth of stress amplitude and displacement amplitude
are plotted below.
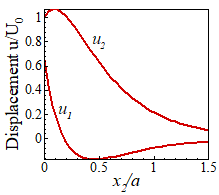
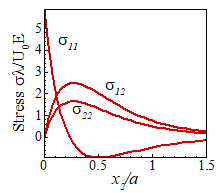
Important
features of this solution are:
- The wave is confined
to a layer near the surface with thickness about twice the
wavelength.
- The horizontal and
vertical components of displacement are 90 degrees out of phase. Material particles therefore describe
elliptical orbits as the wave passes by.
- The speed of the wave
is independent of its wavelength that is to say, the wave is
non-dispersive.
- Rayleigh waves are
exploited in a range of engineering applications, including surface
acoustic wave devices; touch sensors; and miniature linear motors. They are also observed in earthquakes,
although these waves are observed to be dispersive, because of density
variations of the earth’s surface.
Other similar kinds of wave
occur in solids: waves near an interface between two dissimilar elastic solids
are called ‘Stoneley’ waves. There are
also special kinds of waves that occur in thin layers, which behave like
wave-guides.
12.4
Travelling waves in beams
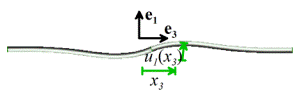 We end our discussion of waves with a
brief look at waves in beams, which show that many of the things we learn about
waves in elementary courses aren’t always true. The figure shows an infinitely
long Euler-Bernoulli beam with Youngs modulus E, mass density , cross sectional area A and inertia components and . The
beam is at rest and has a transverse displacement
We end our discussion of waves with a
brief look at waves in beams, which show that many of the things we learn about
waves in elementary courses aren’t always true. The figure shows an infinitely
long Euler-Bernoulli beam with Youngs modulus E, mass density , cross sectional area A and inertia components and . The
beam is at rest and has a transverse displacement
at time t=0.
Our goal is to find the subsequent motion of the beam.
Start with the equation of motion for the beam:
where
. At
first sight this looks just like the wave equation for a string, but the simple
solution does not satisfy the governing equation. Travelling wave solutions do exist, but only
for very special initial deflections.
For example, if the initial deflection is
where
k is the wave number (related to the
wavelength by ), then the governing equation and initial
conditions are satisfied by a propagating wave solution of the form
Note
that the wave speed turns out to be . This means that the wave speed depends on the
wavelength, and waves with short wavelength propagate faster than those with
long wavelength. Waves of this kind are
called ‘dispersive’. Dispersive waves
are actually more common than the non-dispersive kind, but they are not as well
behaved, so we don’t talk about them in polite company.
We
can use the double-angle formulas to re-write the harmonic traveling wave
solution as
This
tells us the frequency of oscillatory motion at every point on the
beam. The formula relating frequency to wave number k is called the ‘dispersion relation’ for the wave.
The
general solution for an arbitrary initial condition can be found by superposing
the harmonic solutions (for an infinitely long beam, take a Fourier transform
of the initial disturbance; for a beam with finite length use Fourier
series). We won’t discuss this in
detail here, but the figures below compare the motion of an initial disturbance
in a beam (the top figure)
and a string (the bottom figure). You
can clearly see the dispersion in the beam.


12.5
Modeling transient dynamics with FEA
If
you need to run a finite element simulation that involves dynamic loading and
you need to understand wave propagation, it is usually best to do an explicit
dynamic simulation. For a linear elastic
solid, the explicit dynamic algorithm will use a forward-Euler time-stepping
algorithm to integrate the discrete equations of motion with respect to
time. The discrete equations have the
form
where
u is a huge vector of the unknown
nodal displacements, K is the
stiffness matrix (we derived a formula for K
in Chapter 10), and M is a diagonal
mass matrix essentially, the total mass of the solid is
divided up among the nodes. The mass
value assigned to each node is determined by the density and volume of the
elements attached to the node.
In
FEA, equations like this are integrated with the following simple time-stepping
scheme:
1.
At t=0, initialize the displacement and
velocity vectors , and compute the initial acceleration
2.
Then for
successive time steps, calculate the acceleration at the end of the step
3.
Then compute the
displacement and velocity at the end of the step
The details of this process are not important the most important things you need to know
are:
1.
The equations of
motion are integrated using a time-stepping scheme, usually with a fixed time
interval
2.
The algorithm is stable only if the time-step is
smaller than a critical magnitude . The critical time-step is the time required for the
fastest wave to propagate through the smallest element in the mesh.
The
animations below illustrate the instability.
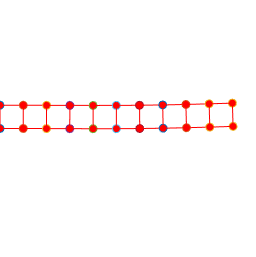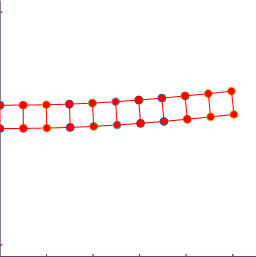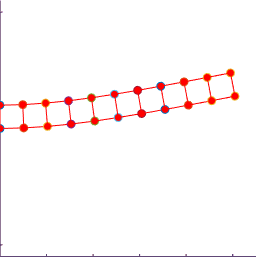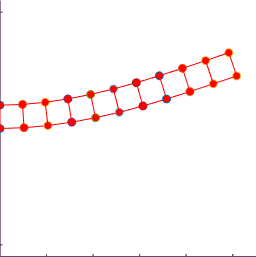
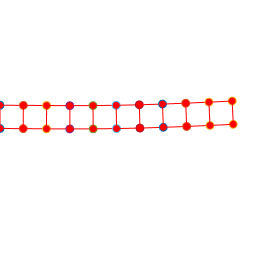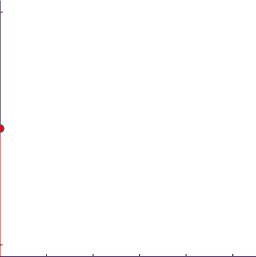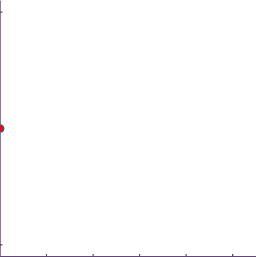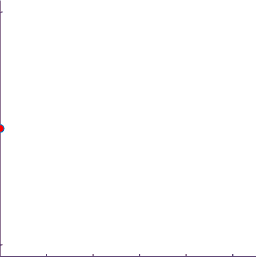
The figure shows a results of a simple MATLAB simulation of the motion
of a beam subjected to a vertical end load (the mesh is coarse, so the
predicted displacements will not be very accurate). The figure on the left is with a time-step
just below the critical value; the figure on the right is for a time-step just
above.
Running explicit dynamic simulations in
ABAQUS
To
set up an explicit dynamic simulation in ABAQUS, use the following steps:
1.
Define a part in
the usual way, and assign properties (and if appropriate a section geometry)
with the property module as usual. You
will need to assign a mass density to the part along with its mechanical
properties. You can do this using the
‘General’ tab in the property editor.
2.
Create an instance
of the part in the usual way.
3.
In the Step
module, select the ‘Dynamic, Explicit’ option.
You can define the time interval for the analysis in the usual way. In the ‘Incrementation’ tab there are some
options to select the time step size. It
is safest to use the ‘Automatic’ option, but it is a good idea to estimate how
many time-steps the simulation is likely to take using the formula for the
critical time step (you will need to know the mesh size, of course, and will
need to be able to estimate the wave speed.
Using the P-wave speed usually gives a safe estimate.)
4.
You can generate
a mesh in the usual way. Note that
choice of element type can be important in dynamic simulations; you are likely
to see hourglassing in some reduced integration elements; and elements that
lock are likely to cause problems.
5.
You can define
boundary conditions the usual way in the Load module. In dynamic simulations, you don’t have to
worry about constraining rigid body modes.
You can also use the ‘Predefined Field’ tab in the ‘Load’ module to
define initial velocity distributions in your part. You can’t define initial displacements. If you need to do this, you will have to run
a separate static step just before the explicit dynamic step, and define the
initial displacement field as boundary conditions in the static step.
6.
Create the job
and run the analysis in the usual way.
The visualization module is identical for static and dynamic analysis.
It
is a good idea to do some hand calculations before you start the calculations
to estimate the stable time-step, and make sure the total analysis time is
short enough for the simulation to complete before you graduate (or if you
already graduated, move to another job or retire).
12.6 Free
vibration of strings and beams
We
can learn about vibrations in solids by studying the behavior of a stretched
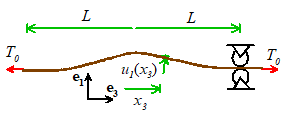
string. 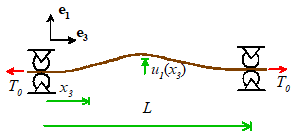 We can start by solving the following problem: a string with length L, mass density and cross-sectional area A under axial tension as at rest and has a transverse displacement
We can start by solving the following problem: a string with length L, mass density and cross-sectional area A under axial tension as at rest and has a transverse displacement
at time t=0.
Find the subsequent motion of the string.
We derived the governing
equation for a string in Chapter 10. It
is
where (this turns out to be is the travelling wave
speed). We already solved this
equation, of course, and could use the traveling wave solution here as
well. But it can be rather painful to
satisfy the boundary conditions with the travelling wave solution, and it is
not easy to visualize the behavior of the solution. It is better to start from scratch, and seek
standing wave solutions to the
equations of motion. We’ll work through
the general procedure:
1.
Find general harmonic solutions to the governing
equation you can usually try solutions of the form .
You will always find a family of possible pairs of that satisfy the equation. For the standard wave equation it’s more
convenient to write the solution in the form
where (by substituting into the wave equation) the
frequencies must satisfy the dispersion relation
2.
The wave numbers must be determined from the boundary
conditions. For our problem we have at
For nonzero solutions to exist the determinant of the
matrix must vanish, which gives where n is
any integer.
3.
Since the
equation system in (2) is now singular, we may discard either of the two
equations and use the other three to determine an equation relating . For the present case we just get the trivial
solution ; with different boundary conditions you will
get more complicated equations.
4.
Finally, we have
to determine the coefficients from the initial conditions (zero velocity and
given initial shape). This gives
The second equation shows that . To
find the coefficients we can use the usual trick to calculate
coefficients of Fourier series: multiply both sides of the equation by (where m
is an integer) and integrate over the length of the string. The integral of the left hand side is zero
for and L/2
for n=m, so
Notice that if we happen to
choose the very special initial deflections
then , and . For
this choice, we will see perfectly harmonic motion
The initial conditions have
excited the vibration mode with natural frequency
We can draw some general
conclusions from this analysis:
Mode
shapes and natural frequencies: The physical significance of the mode shapes and natural frequencies of
a vibrating beam can be visualized as follows:
- Suppose that an
elastic solid (we consider a 1D beam or a string as an example, but the
ideas are the same for 2D and 3D solids) is made to vibrate by bending it
into some (fixed) deformed shape ;
and then suddenly releasing it. In
general, the resulting motion of the solid will be very complicated, and
may not even appear to be periodic (it will be periodic in a string,
however).
- However, there exists
a set of special initial deflections ,
which cause every point on the beam to experience simple harmonic motion
at some (angular) frequency ,
so that the deflected shape has the form .
- The special
frequencies are called the natural frequencies,
and the special initial deflections are called the mode shapes. Each mode shape has a wave
number ,
which characterizes the wavelength of the harmonic vibrations. The formula relating wave number to
frequency depends on the shape of the solid (it is actually the dispersion
relation for the wave). For a
stretched spring, we have the formulas
- The mode shapes have a very useful property as we saw for the string
The
example below will give you some more insight into the nature of vibrations in
flexible solids.
Free vibration of a beam
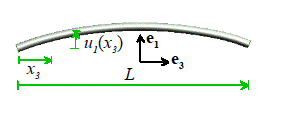 The figure illustrates the problem to be solved: an
initially straight beam, with axis parallel to the direction and principal axes of inertia
parallel to is free of external force. The beam has Young’s
modulus and mass density ,
and its cross-section has area A and
principal moments of area . Its ends may be constrained in various ways,
as described in more detail below. We
wish to calculate the natural frequencies and mode shapes of vibration for the
beam, and to use these results to write down the displacement for a beam that is caused to vibrate with
initial conditions ,
at time t=0.
The figure illustrates the problem to be solved: an
initially straight beam, with axis parallel to the direction and principal axes of inertia
parallel to is free of external force. The beam has Young’s
modulus and mass density ,
and its cross-section has area A and
principal moments of area . Its ends may be constrained in various ways,
as described in more detail below. We
wish to calculate the natural frequencies and mode shapes of vibration for the
beam, and to use these results to write down the displacement for a beam that is caused to vibrate with
initial conditions ,
at time t=0.
Mode
shapes and natural frequencies: The physical significance of the mode shapes and natural frequencies of
a vibrating beam can be visualized as follows:
- Suppose that the beam
is made to vibrate by bending it into some (fixed) deformed shape ;
and then suddenly releasing it. In
general, the resulting motion of the beam will be very complicated, and
may not even appear to be periodic.
- However, there exists
a set of special initial deflections ,
which cause every point on the beam to experience simple harmonic motion
at some (angular) frequency ,
so that the deflected shape has the form .
- The special
frequencies are called the natural frequencies
of the beam, and the special initial deflections are called the mode shapes. Each mode shape has a wave
number ,
which characterizes the wavelength of the harmonic vibrations, and is
related to the natural frequency by
- The mode shapes have a very useful property (which is
proved in Section 5.9.1):
The
mode shapes, wave numbers and corresponding natural frequencies depend on the
way the beam is supported at its ends. A
few representative results are listed below
Beam
with free ends:
The wave numbers for each mode are given by the roots
of the equation
The mode shapes are
where are arbitrary constants.
Beam
with pinned ends:
The wave numbers for each mode are
The mode shapes are ,
where are arbitrary constants
Cantilever
beam (clamped at ,
free at :
The wave numbers for each mode are given by the roots
of the equation
The mode shapes are
where are arbitrary constants.
Vibration
of a beam with given initial displacement and velocity
The
solution for free vibration of a beam with given initial displacement and
velocity can be found by superposing contributions from each mode as follows
where
Derivation: The
deflection of the beam must satisfy the equation of motion given in Chapter 10
1. The general solution to this equation (found, e.g. by
separation of variables, or just by direct substitution) is
where the frequency and wave number must be related by
to satisfy the equation of motion.
2. The coefficients and the wave number must be chosen to satisfy the boundary
conditions at the ends of the bar. For
a beam with free ends, the boundary conditions reduce to ,
at . Substituting the formula from (2) into the
four boundary conditions, and writing the resulting equations in matrix form
yields
3. For a nonzero solution, the matrix in this equation
must be singular. This implies that the
determinant of the matrix is zero, which gives the governing equation for
the wave-number
4. Since the equation system in (3) is now singular, we
may discard any one of the four equations and use the other three to determine
an equation relating to . Choosing to discard the last row of the
matrix, and taking the first column to the right hand side shows that
Solving this equation system shows that . Substituting these values back into the
solution in step (2) gives the mode shape.
5. To understand the formula for the vibration of a beam
with given initial conditions, note that the most general solution consists of
a linear combination of all possible
mode shapes, i.e.
Formulas
for found by substituting ,
multiplying both sides of the equation by and integrating over the length of the
beam. We know that
so
the result reduces to
The
formula for is found by differentiating the general
solution with respect to time to find the velocity, substituting ,
and then proceeding as before to extract each coefficient .
12.7 Calculating
natural frequencies and mode shapes with ABAQUS
It is straightforward to
calculate natural frequencies and mode shapes for elastic solids using ABAQUS.
1.
 Define a part in the usual way, and assign properties
(and if appropriate a section geometry) with the property module as usual. You will need to assign a mass density to
the part along with its mechanical properties.
You can do this using the ‘General’ tab in the property editor.
Define a part in the usual way, and assign properties
(and if appropriate a section geometry) with the property module as usual. You will need to assign a mass density to
the part along with its mechanical properties.
You can do this using the ‘General’ tab in the property editor.
2.
Create an
instance of the part in the usual way.
3.
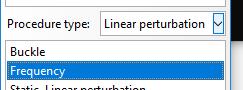
In the Step
module, select the ‘Linear Perturbation’ procedure, and select the ‘Frequency’
option.
4.
In the menu that
comes up next, you can specify the maximum frequency of the vibration mode you
care about this is usually the most useful option for
real design applications but for homework problems we don’t usually have a
reason to look for a particular frequency range so it’s better to specify how
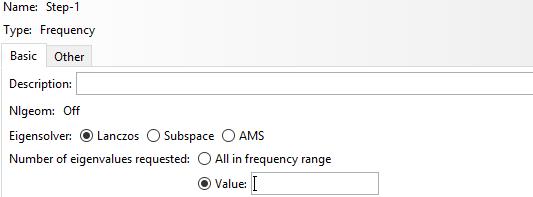
many vibration modes you want to look at for this purpose, check the ‘Value’ radio
button and enter a suitable number of vibration modes into the box. Of course, the more you ask for, the longer
the calculation will take. The higher
frequency modes tend to also need a finer mesh. Usually 30-50 modes is more than enough.
5. 
6.
You can generate
a mesh in the usual way. Note that
choice of element type can be important in dynamic simulations; you are likely
to see hourglassing in some reduced integration elements; and elements that
lock are likely to cause problems.
7.
You can define
boundary conditions the usual way in the Load module. In dynamic simulations, you don’t have to
worry about constraining rigid body modes.
You can also use the ‘Predefined Field’ tab in the ‘Load’ module to
define initial velocity distributions in your part. You can’t define initial displacements. If you need to do this, you will have to run
a separate static step just before the explicit dynamic step, and define the
initial displacement field as boundary conditions in the static step.
8.
Create the job
and run the analysis in the usual way
9.
You can view the
natural frequencies and mode shapes in the Visualization module. The arrows that normally select the increment
number are used to step through the modes.
The deformed shape will show the mode shape (you can see the stresses
associated with the deformation if you are interested; of course the magnitudes
of the stresses are irrelevant, because the amplitude of the mode is
arbitrary). You will see the frequency
displayed in the viewport as well.
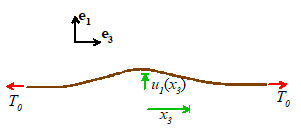 We can learn a lot about the behavior of waves in
solids by looking at the behavior of a stretched string. For this purpose we
solve the following problem: An infinitely
long string under axial tension as at rest and has a transverse displacement
We can learn a lot about the behavior of waves in
solids by looking at the behavior of a stretched string. For this purpose we
solve the following problem: An infinitely
long string under axial tension as at rest and has a transverse displacement
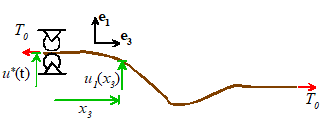 The same general solution can be used to solve any
traveling wave problem. For example,
suppose we hold one end of a very long string.
The string is at rest with everywhere at t=0. We then move the end we
are holding with a prescribed displacement . Find
the displacement.
The same general solution can be used to solve any
traveling wave problem. For example,
suppose we hold one end of a very long string.
The string is at rest with everywhere at t=0. We then move the end we
are holding with a prescribed displacement . Find
the displacement.
 Example 3:
Reflections at a boundary
Example 3:
Reflections at a boundary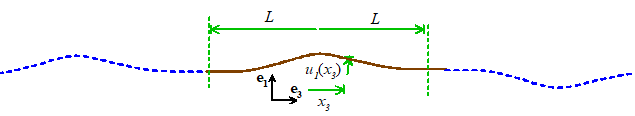


![]() The strain-displacement relation gives
The strain-displacement relation gives![]() The elastic stress-strain law gives
The elastic stress-strain law gives![]() Finally, the linear momentum balance equation
gives
Finally, the linear momentum balance equation
gives![]() is the speed of longitudinal wave propagation
through the solid
is the speed of longitudinal wave propagation
through the solid![]() is the speed of shear wave propagation through
the solid.
is the speed of shear wave propagation through
the solid.

![]() This solution is a cheat, because it doesn’t satisfy
the full 3D equations of elasticity, but it turns out to be quite accurate.
This solution is a cheat, because it doesn’t satisfy
the full 3D equations of elasticity, but it turns out to be quite accurate.  Reflection of waves traveling normal to a free surface
Reflection of waves traveling normal to a free surface

![]() The solid
is an isotropic, linear elastic material with Young’s modulus ,
Poisson’s ratio and mass density
The solid
is an isotropic, linear elastic material with Young’s modulus ,
Poisson’s ratio and mass density ![]() The
solid has shear wave speed and longitudinal wave speed
The
solid has shear wave speed and longitudinal wave speed ![]() The
surface is free of tractions
The
surface is free of tractions![]() A
Rayleigh wave with wavelength propagates in the direction
A
Rayleigh wave with wavelength propagates in the direction

 We end our discussion of waves with a
brief look at waves in beams, which show that many of the things we learn about
waves in elementary courses aren’t always true. The figure shows an infinitely
long Euler-Bernoulli beam with Youngs modulus E, mass density , cross sectional area A and inertia components and . The
beam is at rest and has a transverse displacement
We end our discussion of waves with a
brief look at waves in beams, which show that many of the things we learn about
waves in elementary courses aren’t always true. The figure shows an infinitely
long Euler-Bernoulli beam with Youngs modulus E, mass density , cross sectional area A and inertia components and . The
beam is at rest and has a transverse displacement



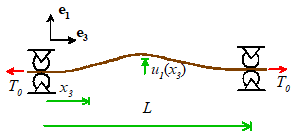 We can start by solving the following problem: a string with length L, mass density and cross-sectional area A under axial tension as at rest and has a transverse displacement
We can start by solving the following problem: a string with length L, mass density and cross-sectional area A under axial tension as at rest and has a transverse displacement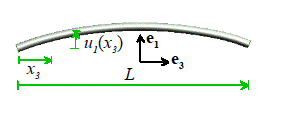 The figure illustrates the problem to be solved: an
initially straight beam, with axis parallel to the direction and principal axes of inertia
parallel to is free of external force. The beam has Young’s
modulus and mass density ,
and its cross-section has area A and
principal moments of area . Its ends may be constrained in various ways,
as described in more detail below. We
wish to calculate the natural frequencies and mode shapes of vibration for the
beam, and to use these results to write down the displacement for a beam that is caused to vibrate with
initial conditions ,
at time t=0.
The figure illustrates the problem to be solved: an
initially straight beam, with axis parallel to the direction and principal axes of inertia
parallel to is free of external force. The beam has Young’s
modulus and mass density ,
and its cross-section has area A and
principal moments of area . Its ends may be constrained in various ways,
as described in more detail below. We
wish to calculate the natural frequencies and mode shapes of vibration for the
beam, and to use these results to write down the displacement for a beam that is caused to vibrate with
initial conditions ,
at time t=0. Define a part in the usual way, and assign properties
(and if appropriate a section geometry) with the property module as usual. You will need to assign a mass density to
the part along with its mechanical properties.
You can do this using the ‘General’ tab in the property editor.
Define a part in the usual way, and assign properties
(and if appropriate a section geometry) with the property module as usual. You will need to assign a mass density to
the part along with its mechanical properties.
You can do this using the ‘General’ tab in the property editor.

