Chapter 8
Small Strain Static Solutions for Elastic
Solids
In
many engineering applications, the component or solid of interest is stiff, and
is subjected only to modest stresses.
This is because large stresses, and large shape changes, usually cause a
component to fail. Stiff solids subjected
to modest loads experience only small changes in shape, and the material can be
assumed to deform elastically. Under
these conditions, it is often possible to calculate exactly the distributions
of stress and strain in the solid.
Analysis of this kind is called ‘linear elasticity.’
In
this chapter, we present a very brief survey of the field of linear
elasticity. Specifically,
1. We will outline some important general features of
solutions to for linear elastic solids subjected to external forces;
2. We will discuss some solution techniques and present
solutions to a few selected problems of interest;
3. We will discuss energy methods for solving problems
involving linear elastic solids. These
will later be used to develop the finite element method for calculating
stresses in elastic solids.
8.1 Summary
of the governing equations of linear elasticity
For a stiff solid subjected
to modest stresses, we can assume
1. All
displacements are small. This means that we can use the infinitesimal
strain tensor to characterize deformation; we do not need to distinguish
between stress measures, and we do not need to distinguish between deformed and
undeformed configurations of the solid when writing equilibrium equations and
boundary conditions.
2. The material is a linear elastic solid. In most practical applications, we can also
assume the material is isotropic, with Young’s modulus E and Poisson’s ratio ,
and mass density .
In any application, we must
be given:
1.
The shape of the
solid in its unloaded condition
2.
The initial
stress field in the solid (we will take this to be zero)
3.
 The elastic constants for the solid and its mass density
The elastic constants for the solid and its mass density
4. The thermal expansion coefficients for the solid, and
temperature change from the initial configuration
5. A body force distribution (per unit mass) acting on the solid
6. Boundary conditions, specifying displacements on a portion or tractions on a portion of the boundary of R
Our
goal is then to calculate the displacement field ,
the strain field and the stress field satisfying the following equations:
 Displacementstrain relation or
Displacementstrain relation or
 The Stressstrain-temperature
relation
The Stressstrain-temperature
relation
or, for an isotropic material:
 Equilibrium
Equation or
Equilibrium
Equation or
 Traction
boundary conditions on parts of the boundary where tractions are
known.
Traction
boundary conditions on parts of the boundary where tractions are
known.
 Displacement
boundary conditions on
parts of the boundary where displacements are known.
Displacement
boundary conditions on
parts of the boundary where displacements are known.
Before actually solving
these equations, we will discuss some general features of the solutions.
8.2
Superposition and linearity of solutions
The
governing equations of elasticity are linear. This has two important consequences:
1. The stresses, strains and displacements in a solid are
directly proportional to the loads (or displacements) applied to the
solid.
2. If you can find two sets of displacements, strains and
stresses that satisfy the governing equations, you can add them to create more
solutions.
These
principles can be illustrated clearly using some of the simple solutions
derived in the next section. For
example, examine the solution to the pressurized sphere (Sect 4.1.4). As an example, the radial stress induced by
pressure on the interior, and zero pressure on the
exterior surface is
The radial stress induced by pressure on the exterior surface, with zero pressure on
the interior surface is
Note
that in both cases the stress is directly proportional to the pressure. In addition, to find the radial stress by
combined pressures on the interior and on the exterior surface, you can just add
these two solutions.
8.3 Uniqueness and existence of solutions to the
linear elasticity equations
The following results are
useful:
1. If only displacements are prescribed on the boundary
of the solid, the governing equations of linear elasticity always have a
solution, and the solution is unique.
2. If mixed boundary conditions are specified, a static
solution exists and is unique if the displacements constrain rigid motions. A
dynamic solution always exists and is unique, provided the velocity field and
displacement field at time t=0
are known.
3. If only tractions are prescribed on the boundary, a
static solution exists only if the tractions are in equilibrium. In this case, the stresses and strains are
unique, but the displacements are not. A
dynamic solution always exists and is unique, again, providing initial
conditions are known.
8.4 Saint-Venant’s principle
Saint-Venant’s
principle is often invoked to justify approximate solutions to boundary value
problems in linear elasticity. For
example, when we solve problems involving bending or axial deformation of
slender beams and rods in elementary strength of materials courses, we only
specify the resultant forces acting on the ends of a rod, or the magnitudes of
point forces acting on a beam, we don’t specify the distribution of traction in
detail. We rely on Saint Venant’s
principle to justify this approach. In this context, the principle states the
following.
The stresses,
strains and displacements far from the ends of a rod or beam subjected to end
loading depend only on the resultant forces and moments acting on its ends, and
do not depend on how the tractions themselves are distributed.
Although
SVP is widely used, it turns out to be remarkably difficult to prove
mathematically. The difficulty is
partly that it is not easy to state the principle itself precisely enough to
apply any mathematical machinery to it. A
rigorous statement is given by Sternberg (Q. J. Appl. Mech 11 p. 393 1954), among several other versions. Here, we will just illustrate the most common
applications of the principle through specific examples.
One
version of SVP can be stated as follows.
Suppose that
we calculate the stress, strain and displacement induced in a solid by two
different traction distributions and that act on some small region of a solid with
characteristic size a. If the tractions
exert the same resultant force and moment, then the stresses, strains and
displacements induced by the two traction distributions at a distance r from
the loaded region are identical for large .
In practice `large’ usually means .
This
principle can be illustrated using a simple example.
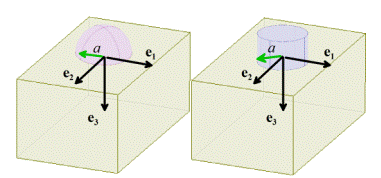
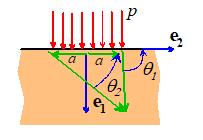
Consider a large solid with a flat surface, as shown in
the picture. It is possible to calculate
formulas for the stresses and displacements induced by various pressure
distributions acting on the flat surface the procedure to do this will be outlined
later. For now, we will compare the
stresses induced by
1.
A uniform pressure
2.
A parabolic pressure
You can verify for yourself that both pressure
distributions exert a resultant force P
acting in the vertical direction on the surface, and exert zero moment about
the origin. The variation of stress down
the axis of symmetry ( ), expressed in cylindrical-polar coordinates,
can be derived as
Case 1: Uniform pressure
Case 2: Parabolic pressure
Now, to demonstrate SVP, we
want to show that the stresses are equal for large z/a. We can do this
graphically the figures below compare the variation of
vertical and radial stress down the axis of symmetry with z/a.
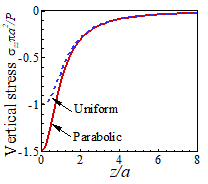
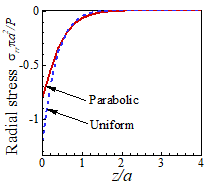
The
stresses induced by the two different pressures are clearly indistinguishable
for . This example helps to quantify what we mean
by a `large’ distance.
The
second commonly used application of SVP is a rather vague statement that
A localized geometrical feature with
characteristic size R in a large solid only influences the stress in a region
with size approximately 3R surrounding the feature.
This
is more a rule of thumb than a precise mathematical statement. It can be illustrated by looking at specific
solutions. For example, the figure below
shows the Mises stress contours surrounding a circular hole in a thin
rectangular plate that is subjected to extensional loading (calculated using the
finite element method). Far from the hole, the stress is uniform. The contours deviate from the uniform
solution in a region that is about three times the hole radius.
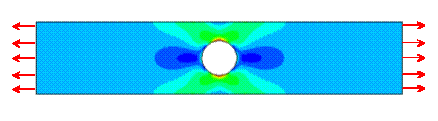
8.5 Simplified equations for
spherically symmetric linear elasticity problems
It is easiest to solve the linear elasticity problems if the
solid of interest has symmetry of some kind, and is subjected to simple
loading. Spheres and cylinders are two
examples.
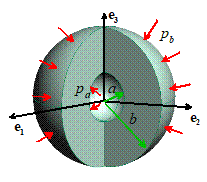
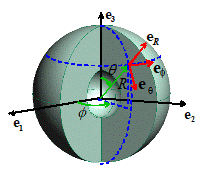 A representative spherically
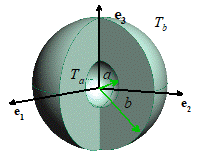
symmetric problem is illustrated in the picture. We consider a hollow, spherical solid, which
is subjected to spherically symmetric loading (i.e. internal body forces, as
well as tractions or displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be
spherically symmetric (a function of R
only).
A representative spherically
symmetric problem is illustrated in the picture. We consider a hollow, spherical solid, which
is subjected to spherically symmetric loading (i.e. internal body forces, as
well as tractions or displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be
spherically symmetric (a function of R
only).
The solution is most conveniently expressed using a
spherical-polar coordinate system, illustrated in the figure. The general procedure for solving problems using
spherical and cylindrical coordinates is complicated, and is discussed in
detail in Appendix E. In this section,
we summarize the special form of these equations for spherically symmetric
problems.
As usual, a point in the solid is identified by its
spherical-polar co-ordinates .
All vectors and tensors are expressed as components in the basis shown in the figure. For a spherically symmetric problem
 Position Vector
Position Vector
 Displacement
vector
Displacement
vector
 Body
force vector
Body
force vector
Here,
and are scalar functions. The stress and strain
tensors (written as components in ) have the form
and
furthermore must satisfy .
The tensor components have exactly the same physical interpretation as they did
when we used a fixed basis, except that the subscripts (1,2,3) have
been replaced by .
For
spherical symmetry, the governing equations of linear elasticity reduce to
 Strain Displacement Relations
Strain Displacement Relations
 StressStrain relations
StressStrain relations
 Equilibrium Equations
Equilibrium Equations
 Boundary Conditions
Boundary Conditions
Prescribed Displacements
Prescribed Tractions
These results can be derived as a special case of the general
3D equations of linear elasticity in spherical coordinates. The details are left as an exercise.
8.6 General solution to the
spherically symmetric linear elasticity problem
Our goal is to solve the equations given in Section 8.5 for
the displacement, strain and stress in the sphere. To do so,
1.
Substitute
the strain-displacement relations into the stress-strain law to show that
2.
Substitute
this expression for the stress into the equilibrium equation and rearrange the
result to see that
Given the temperature distribution and body force this
equation can easily be integrated to calculate the displacement u.
Two arbitrary constants of integration will appear when you do the
integral these must be determined from the boundary conditions at the inner and
outer surface of the sphere.
Specifically, the constants must be selected so that either the
displacement or the radial stress have prescribed values on the inner and outer
surface of the sphere.
In the following sections, this procedure is used to derive
solutions to various boundary value problems of practical interest.
8.7 Examples of solutions to the
spherically symmetric linear elasticity problem
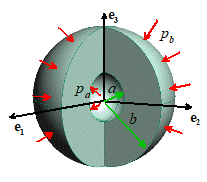 Example
1: Pressurized hollow sphere
Example
1: Pressurized hollow sphere
Assume
that
 No body forces act on the sphere
No body forces act on the sphere
 The sphere has uniform temperature
The sphere has uniform temperature
 The inner surface R=a is subjected to pressure
The inner surface R=a is subjected to pressure
 The outer surface R=b is subjected to pressure
The outer surface R=b is subjected to pressure
Show that
the displacement, strain and stress fields in the sphere are
Solution: The solution can be found by applying the procedure outlined
in Sect 4.1.3.
1.
Note
that the governing equation for u (Sect
4.1.3) reduces to
2.
Integrating
twice gives
where A and B are constants of integration to be
determined.
3.
The
radial stress follows by substituting into the stress-displacement formulas
4. To satisfy the boundary conditions, A and B must be chosen so that and (the stress is negative because the pressure
is compressive). This gives two
equations for A and B that are easily solved to find
5.
Finally,
expressions for displacement, strain and stress follow by substituting for A and B in the formula for u
in (2), and using the formulas for strain and stress in terms of u in Section 4.1.2.
 Example
2: Gravitating sphere
Example
2: Gravitating sphere
A planet under its own gravitational attraction may be
idealized (rather crudely) as a solid sphere with radius a, with the following loading
 A body force per unit mass, where g is the acceleration due to
gravity at the surface of the sphere
A body force per unit mass, where g is the acceleration due to
gravity at the surface of the sphere
 A uniform temperature distribution
A uniform temperature distribution
 A traction free surface at R=a
A traction free surface at R=a
Show that
the displacement, strain and stress in the sphere follow as
Solution:
1.
Begin
by writing the governing equation for u
given in 4.1.3 as
2.
Integrating
where A and B are constants of integration that must be determined
from boundary conditions.
3.
The
radial stress follows from the formulas in 4.1.3 as
4.
Finally,
the constants A and B can be determined as follows: (i) The
stress must be finite at ,
which is only possible if . (ii) The surface of the sphere is traction
free, which requires at R=a. Substituting the latter condition into the
formula for stress in (3) and solving for A
gives
5.
The
final formulas for stress and strain follow by substituting the result of (4)
back into (2), and using the formulas in Section 4.1.2.
 Example 3: Sphere with steady state heat flow
Example 3: Sphere with steady state heat flow
The deformation and stress in a sphere that is heated on the
inside (or outside), and has reached its steady state temperature distribution
can be calculated as follows. Assume
that
 No body force acts on the sphere
No body force acts on the sphere
 The temperature distribution in the sphere is
The temperature distribution in the sphere is
where and are the temperatures at the inner and outer
surfaces. The total rate of heat loss
from the sphere is ,
where k is the thermal conductivity.
 The surfaces at R=a and R=b are traction free.
The surfaces at R=a and R=b are traction free.
Show that
the displacement, strain and stress fields in the sphere follow are
Solution:
1.
The
differential equation for u reduces
to
2.
Integrating
where A and B are constants of integration.
3.
The
radial stress follows from the formulas as
4.
The
boundary conditions require that at r=a
and r=b. Substituting these conditions into the result
of step (3) gives two equations for A
and B which can be solved to see that
8.8 Simplified equations for axially
symmetric linear elasticity problems
 Two examples of axially symmetric
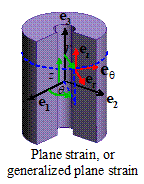
problems are illustrated in the picture.
In both cases the solid is a circular cylinder, which is subjected to
axially symmetric loading (i.e. internal body forces, as well as tractions or
displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be axially
symmetric (a function of r
only). Finally, the solid can spin with
steady angular velocity about the axis.
Two examples of axially symmetric
problems are illustrated in the picture.
In both cases the solid is a circular cylinder, which is subjected to
axially symmetric loading (i.e. internal body forces, as well as tractions or
displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be axially
symmetric (a function of r
only). Finally, the solid can spin with
steady angular velocity about the axis.
The two solids have different shapes. In the first case, the length of the cylinder
is substantially greater than any cross-sectional dimension. In the second case, the length of the
cylinder is much less than its outer radius.
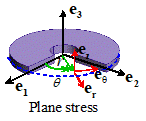 The state of stress and strain in the
solid depends on the loads applied to the ends of the cylinder. Specifically
The state of stress and strain in the
solid depends on the loads applied to the ends of the cylinder. Specifically
 If the cylinder is completely prevented from
stretching in the direction a state of plane strain exists in the solid.
This is an exact solution to the 3D equations of elasticity, is valid
for a cylinder with any length, and is accurate everywhere in the cylinder.
If the cylinder is completely prevented from
stretching in the direction a state of plane strain exists in the solid.
This is an exact solution to the 3D equations of elasticity, is valid
for a cylinder with any length, and is accurate everywhere in the cylinder.
 If the top and bottom surface of the short
plate-like cylinder are free of traction, a state of plane stress exists in the solid.
This is an approximate solution to the 3D equations of elasticity, and
is accurate only if the cylinder’s length is much less than its diameter.
If the top and bottom surface of the short
plate-like cylinder are free of traction, a state of plane stress exists in the solid.
This is an approximate solution to the 3D equations of elasticity, and
is accurate only if the cylinder’s length is much less than its diameter.
 If the top and bottom ends of the long cylinder are subjected to a
prescribed force (or the ends are free of force) a state of generalized plane strain exists in the
cylinder. This is an approximate
solution, which is accurate only away from the ends of a long cylinder. As a rule of thumb, the solution is
applicable approximately three cylinder radii away from the ends.
If the top and bottom ends of the long cylinder are subjected to a
prescribed force (or the ends are free of force) a state of generalized plane strain exists in the
cylinder. This is an approximate
solution, which is accurate only away from the ends of a long cylinder. As a rule of thumb, the solution is
applicable approximately three cylinder radii away from the ends.
The solution is most conveniently expressed using a
spherical-polar coordinate system, illustrated in the figure. A point in the solid is identified by its
spherical-polar co-ordinates .
All vectors and tensors are expressed as components in the basis shown in the figure. For an axially symmetric problem
 Position
Vector
Position
Vector
 Displacement vector
Displacement vector
 Body force vector
Body force vector
 Acceleration vector
Acceleration vector
Here, and are scalar functions.
The stress and strain
tensors (written as components in ) have the form
For
axial symmetry, the governing equations of linear elasticity reduce to
 Strain Displacement Relations
Strain Displacement Relations
 StressStrain relations
(plane strain and generalized plane strain)
StressStrain relations
(plane strain and generalized plane strain)
where for plane strain, and constant for generalized
plane strain.
 StressStrain relations
(plane stress)
StressStrain relations
(plane stress)
 Equation of motion
Equation of motion
 Boundary Conditions
Boundary Conditions
Prescribed Displacements
Prescribed Tractions
Plane strain solution
Generalized plane strain solution, with
axial force applied to cylinder:
These results can either be derived as a special case of the
general 3D equations of linear elasticity in spherical coordinates. The details are left as an exercise.
8.9 General solution to the axisymmetric boundary value problem
Our goal
is to solve the equations given in Section 4.1.2 for the displacement, strain
and stress in the sphere. To do so,
1.
Substitute
the strain-displacement relations into the stress-strain law to show that, for
generalized plane strain
where is constant.
The equivalent expression for plane stress is
2.
Substitute
these expressions for the stress into the equilibrium equation and rearrange
the result to see that, for generalized plane strain
while for plane stress
Given the temperature distribution and body force these
equations can be integrated to calculate the displacement u. Two arbitrary constants
of integration will appear when you do the integral these must be determined from the boundary conditions at the inner and
outer surface of the sphere.
Specifically, the constants must be selected so that either the
displacement or the radial stress have prescribed values on the inner and outer
surface of the sphere. Finally, for the
generalized plane strain solution, the axial strain must be determined, using the equation for the
axial force acting on the ends of the cylinder.
In the following sections, this procedure is used to derive
solutions to various boundary value problems of practical interest.
8.10 Example solutions for cylindrically symmetric solids
Example 1: Long
(generalized plane strain) cylinder subjected to internal and external
pressure.
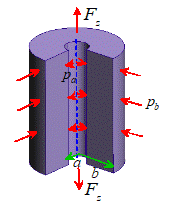
We consider a long hollow
cylinder with internal radius a and
external radius b as shown in the
figure.
Assume
that
 No body forces act on the cylinder
No body forces act on the cylinder
 The cylinder has zero angular velocity
The cylinder has zero angular velocity
 The sphere has uniform temperature
The sphere has uniform temperature
 The inner surface r=a is subjected to pressure
The inner surface r=a is subjected to pressure
 The outer surface r=b is subjected to pressure
The outer surface r=b is subjected to pressure
 For the plane strain solution, the cylinder
does not stretch parallel to its axis.
For the generalized plane strain solution, the ends of the cylinder are
subjected to an axial force as shown.
In particular, for a closed ended
cylinder the axial force exerted by the pressure inside the cylinder acting on
the closed ends is
For the plane strain solution, the cylinder
does not stretch parallel to its axis.
For the generalized plane strain solution, the ends of the cylinder are
subjected to an axial force as shown.
In particular, for a closed ended
cylinder the axial force exerted by the pressure inside the cylinder acting on
the closed ends is
The displacement, strain
and stress fields in the cylinder are
where for plane strain, while
for generalized plane strain.
Derivation: These
results can be derived as follows. The
governing equation reduces to
The equation
can be integrated to see that
The radial stress follows as
The
boundary conditions are (the stresses are negative because the
pressure is compressive). This yields
two equations for A and B that area easily solved to see that
The remaining results follow
by elementary algebraic manipulations.
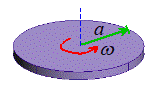 Example 2: Spinning circular plate
Example 2: Spinning circular plate
We consider a thin solid plate with radius a that spins with angular speed about its axis. Assume that
 No body forces act on the disk
No body forces act on the disk
 The disk has constant angular velocity
The disk has constant angular velocity
 The disk has uniform temperature
The disk has uniform temperature
 The outer surface r=a and the top and bottom faces of the disk are free of traction.
The outer surface r=a and the top and bottom faces of the disk are free of traction.
 The disk is sufficiently thin to ensure a
state of plane stress in the disk.
The disk is sufficiently thin to ensure a
state of plane stress in the disk.
Derivation: To derive these results, recall that
the governing equation is
The equation
can be integrated to see that
The radial
stress follows as
The radial
stress must be bounded at r=0, which
is only possible if B=0. In addition, the radial stress must be zero
at r=a, which requires that
The
remaining results follow by straightforward algebra.
Example 3: Stresses
induced by an interference fit between two cylinders
Interference
fits are often used to secure a bushing or a bearing housing to a shaft. In this problem we calculate the stress
induced by such an interference fit.
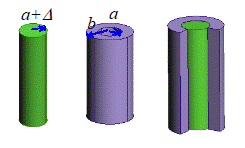
Consider
a hollow cylindrical bushing, with outer radius b and inner radius a. Suppose that a solid shaft with radius ,
with is inserted into the cylinder as shown. (In practice, this is done by heating the
cylinder or cooling the shaft until they fit, and then letting the system
return to thermal equilibrium)
 No body forces act on the solids
No body forces act on the solids
 The angular velocity is zero
The angular velocity is zero
 The cylinders have uniform temperature
The cylinders have uniform temperature
 The shaft slides freely inside the bushing
The shaft slides freely inside the bushing
 The ends of the cylinder are free of force.
The ends of the cylinder are free of force.
 Both the shaft and cylinder have the same
Young’s modulus E and Poisson’s ratio
Both the shaft and cylinder have the same
Young’s modulus E and Poisson’s ratio
 The cylinder and shaft are sufficiently long
to ensure that a state of generalized plane strain can be developed in each
solid.
The cylinder and shaft are sufficiently long
to ensure that a state of generalized plane strain can be developed in each
solid.
The
displacements, strains and stresses in the solid shaft (r<a) are
In the hollow cylinder,
they are
Derivation: These results can be derived using
the solution to a pressurized cylinder given in Section 4.1.9. After the shaft
is inserted into the tube, a pressure p
acts to compress the shaft, and the same pressure pushes outwards to expand the
cylinder. Suppose that this pressure
induces a radial displacement in the solid cylinder, and a radial
displacement in the hollow tube. To accommodate the interference, the
displacements must satisfy
Evaluating
the relevant displacements using the formulas in 4.1.9 gives
Here, we
have assumed that the axial force acting on both the shaft and the tube must
vanish separately, since they slide freely relative to one another. Solving these two equations for p shows that
8.11 Airy Function Solution to Plane Stress and Strain
Static Linear Elastic Problems
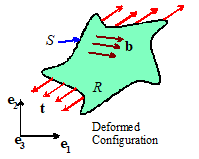 In this section we outline a general
technique for solving 2D static linear elasticity problems. The technique is known as the `Airy Stress
Function’ method.
In this section we outline a general
technique for solving 2D static linear elasticity problems. The technique is known as the `Airy Stress
Function’ method.
A typical plane elasticity problem is illustrated in the picture. The solid is two dimensional, which means
either that
1. The solid is a thin sheet, with small
thickness h, and is loaded only in
the plane.
In this case the plane stress
solution is applicable
2. The solid is very long in the direction, is prevented from stretching
parallel to the axis, and every cross section is loaded
identically and only in the plane.
In this case, the plane strain
solution is applicable.
Some
additional basic assumptions and restrictions are:
 The Airy stress function is applicable only to
isotropic solids. We will assume that the solid has Young’s modulus E, Poisson’s ratio and mass density
The Airy stress function is applicable only to
isotropic solids. We will assume that the solid has Young’s modulus E, Poisson’s ratio and mass density
 The Airy Stress function can only be used if the body
force has a special form. Specifically,
the requirement is
The Airy Stress function can only be used if the body
force has a special form. Specifically,
the requirement is
where is a scalar function of position. Fortunately, most practical body forces can
be expressed in this form, including gravity.
 The
Airy Stress Function approach works best for problems where a solid is
subjected to prescribed tractions on its boundary, rather than prescribed
displacements. Specifically, we will
assume that the solid is loaded by boundary tractions .
The
Airy Stress Function approach works best for problems where a solid is
subjected to prescribed tractions on its boundary, rather than prescribed
displacements. Specifically, we will
assume that the solid is loaded by boundary tractions .
The Airy solution in rectangular
coordinates
The Airy
function procedure can then be summarized as follows:
1. Begin by finding a scalar function (known as the Airy potential) which satisfies:
where
In addition  must satisfy the
following traction boundary conditions on the surface of the solid
must satisfy the
following traction boundary conditions on the surface of the solid
where
are the components of a unit vector normal to
the boundary.
2. Given  , the stress field within the region of interest can be
calculated from the formulas
, the stress field within the region of interest can be
calculated from the formulas
3. If the strains are needed, they may be computed from
the stresses using the elastic stressstrain relations.
4. If the displacement field is needed, it may be
computed by integrating the strains, following the procedure described in
Section 2.1.20. An example (in polar
coordinates) is given in Section 5.2.4 below.
Although
it is easier to solve for  than it is to solve
for stress directly, this is still not a trivial exercise. Usually, one guesses a suitable form for
than it is to solve
for stress directly, this is still not a trivial exercise. Usually, one guesses a suitable form for  , as illustrated below.
This may seem highly unsatisfactory, but remember that we are
essentially integrating a system of PDEs.
The general procedure to evaluate any integral is to guess a solution,
differentiate it, and see if the guess was correct.
, as illustrated below.
This may seem highly unsatisfactory, but remember that we are
essentially integrating a system of PDEs.
The general procedure to evaluate any integral is to guess a solution,
differentiate it, and see if the guess was correct.
Demonstration that the Airy solution
satisfies the governing equations
Recall
that to solve a linear elasticity problem, we need to satisfy the following
equations:
 Displacementstrain relation
Displacementstrain relation
 Stressstrain relation
Stressstrain relation
 Equilibrium
Equation
Equilibrium
Equation
where we have
neglected thermal expansion, for simplicity.
The Airy function is chosen so as to satisfy the equilibrium
equations automatically. For plane
stress or plane strain conditions, the equilibrium equations reduce to
Substitute for the stresses
in terms of  to see that
to see that
so
that the equilibrium equations are satisfied automatically for any choice of  . To ensure that the
other two equations are satisfied, we first compute the strains using the
elastic stress-strain equations. Recall
that
. To ensure that the
other two equations are satisfied, we first compute the strains using the
elastic stress-strain equations. Recall
that
with for plane stress and for plane strain. Hence
Next,
recall that the straindisplacement
relation is satisfied provided that the strains obey the compatibility
conditions
All
but the first of these equations are satisfied automatically by any plane
strain or plane stress field. Substitute into the first equation in terms of
stress to see that
Finally,
substitute into this horrible looking equation for stress in terms of  and rearrange to see
that
and rearrange to see
that
A few more weeks of algebra
reduces this to
which is the result we were
looking for.
This
proves that the Airy representation satisfies the governing equations. A second important question is is it possible to find an Airy function for all 2D plane stress and plane strain
problems? If not, the method would be
useless, because you couldn’t tell ahead of time whether existed for the problem you were trying to
solve. Fortunately it is possible to
prove that all properly posed 2D elasticity problems do have an Airy
representation.
The Airy solution in cylindrical-polar
coordinates
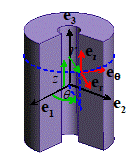
Boundary
value problems involving cylindrical regions are best solved using Cylindrical-polar
coordinates. It is worth recording the
Airy function equations for this coordinate system.
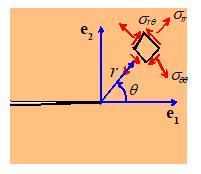
In
a 2D cylindrical-polar coordinate system, a point in the solid is specified by
its radial distance from the origin and the angle . The solution is independent of z.
The Airy function is written as a function of the coordinates as . Vector quantities (displacement, body force)
and tensor quantities (strain, stress) are expressed as components in the basis
shown in the picture.
The governing equation for
the Airy function in this coordinate system is
The state of stress is
related to the Airy function by
In polar coordinates the
strains are related to the stresses by
for plane strain, while
for
plane stress. The displacements must be
determined by integrating these strains following the procedure similar to that
outlined in Section 2.1.20. To this end,
let denote the displacement vector. The strain-displacement relations in polar
coordinates are:
These
can be integrated using a procedure analogous to that outlined in Section
2.1.20. An example is given in Section
5.2.5.
In
the following sections, we give several examples of Airy function solutions to
boundary value problems.
8.12 Examples of Airy Function Solutions to plane
problems in linear elasticity
Example 1: Airy function solution to the end loaded
cantilever
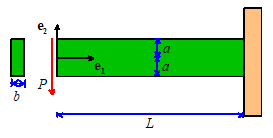 Consider a cantilever beam, with length L, height 2a and out-of-plane thickness b,
as shown in the figure. The beam is made from an isotropic linear elastic solid
with Young’s modulus and Poisson ratio .
The top and bottom of the beam are traction free, the left hand end is
subjected to a resultant force P, and
the right hand end is clamped. Assume
that b<<a, so that a state of
plane stress is developed in the beam. An approximate solution to the stress in
the beam can be calculated from the Airy function
Consider a cantilever beam, with length L, height 2a and out-of-plane thickness b,
as shown in the figure. The beam is made from an isotropic linear elastic solid
with Young’s modulus and Poisson ratio .
The top and bottom of the beam are traction free, the left hand end is
subjected to a resultant force P, and
the right hand end is clamped. Assume
that b<<a, so that a state of
plane stress is developed in the beam. An approximate solution to the stress in
the beam can be calculated from the Airy function
You
can easily show that this function satisfies the governing equation for the
Airy function. The stresses follow as
To see that this solution
satisfies the boundary conditions, note that
1. The top and bottom surfaces of the beam are traction free ( ).
Since the normal is in the direction on these surfaces, this requires
that . The stress field clearly satisfies this
condition.
2. The plane stress assumption automatically satisfies
boundary conditions on .
3. The traction boundary condition on the left hand end
of the beam ( ) was not specified in detail: instead, we
only required that the resultant of the traction acting on the surface is . The normal to the surface at the left hand
end of the beam is in the direction, so the traction vector is
The resultant force can be calculated by integrating
the traction over the end of the beam:
The stresses thus satisfy the boundary condition. Note that by Saint-Venant’s principle, other
distributions of traction with the same resultant will induce the same stresses
sufficiently far ( ) from the end of the beam.
4. The boundary conditions on the right hand end of the
beam are not satisfied exactly. The exact solution should satisfy both and on . The displacement field corresponding to the
stress distribution was calculated in the example problem in Sect 2.1.20, where
we found that
where are constants that may be selected to satisfy
the boundary condition as far as possible.
We can satisfy and at some, but not all, points on . The choice is arbitrary. Usually the boundary condition is
approximated by requiring at ,
. This gives ,
and . By Saint-Venant’s principle, applying other
boundary conditions (including the exact boundary
condition) will not influence the stresses and displacements sufficiently far
from the end.
Example 2: 2D Line load acting perpendicular to the
surface of an infinite solid
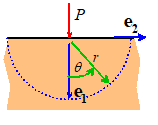
As
a second example, the stress fields due to a line load magnitude P per
unit out-of-plane length acting on the surface of a homogeneous, isotropic
half-space can be generated from the Airy function
The formulas in the preceding
section yield
The stresses in the basis are
The
method outlined in section 5.2.3 can be used to calculate the displacements:
the procedure is described in detail below to provide a representative
example. For plane strain deformation,
we find
to
within an arbitrary rigid motion. Note
that the displacements vary as log(r) so they are unbounded both at the origin
and at infinity. Moreover, the
displacements due to any distribution of traction that exerts a nonzero
resultant force on the surface will also be unbounded at infinity.
It
is easy to see that this solution satisfies all the relevant boundary
conditions. The surface is traction free
( ) except at r=0. To see that the
stresses are consistent with a vertical point force, note that the resultant
vertical force exerted by the tractions acting on the dashed curve shown in the
picture can be calculated as
The
expressions for displacement can be derived as follows. Substituting the expression for stress into
the stress-strain laws and using the strain-displacement relations yields
Integrating
where is a function of to be determined. Similarly, considering the hoop stresses
gives
Rearrange and integrate
with respect to
where
is a function of to be determined. Finally, substituting for stresses into the
expression for shear strain shows that
Inserting the expressions
for displacement and simplifying gives
The
two terms in parentheses are functions of and r,
respectively, and so must both be separately equal to zero to satisfy this
expression for all possible values of and r.
Therefore
This ODE has solution
The second equation gives
which
has solution . The constants A,B,C represent an arbitrary rigid displacement, and can be taken
to be zero. This gives the required
answer.
Example 3: 2D Line load acting parallel to the surface
of an infinite solid
Similarly,
the stress fields due to a line load magnitude P per unit out-of-plane
length acting tangent to the surface of a homogeneous, isotropic half-space can
be generated from the Airy function
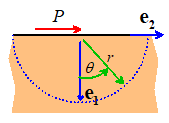 The formulas in the preceding section yield
The formulas in the preceding section yield
The
method outlined in the preceding section can be used to calculate the
displacements. The procedure gives
to
within an arbitrary rigid motion.
The stresses and
displacements in the basis are
 Example
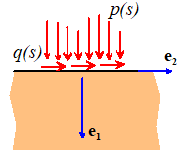
4: Arbitrary pressure acting on a flat surface
Example
4: Arbitrary pressure acting on a flat surface
The
principle of superposition can be used to extend the point force solutions to
arbitrary pressures acting on a surface. For example, we can find the (plane
strain) solution for a uniform pressure acting on the strip of width 2a
on the surface of a half-space by distributing the point force solution
appropriately.
Distributing
point forces with magnitude over the loaded region shows that
Example 5: Uniform normal pressure acting on a strip
 For the particular case of a uniform pressure, the
integrals can be evaluated to show that
For the particular case of a uniform pressure, the
integrals can be evaluated to show that
where and
Example 6: Stresses near the tip of a
crack
 Consider an infinite solid, which contains a
semi-infinite crack on the (x1,x3) plane.
Suppose that the solid deforms in plane strain and is subjected to bounded
stress at infinity. The stress field
near the tip of the crack can be derived from the Airy function
Consider an infinite solid, which contains a
semi-infinite crack on the (x1,x3) plane.
Suppose that the solid deforms in plane strain and is subjected to bounded
stress at infinity. The stress field
near the tip of the crack can be derived from the Airy function
Here,
and are two constants, known as mode I and mode II stress intensity factors,
respectively. They quantify the
magnitudes of the stresses near the crack tip, as shown below. Their role will
be discussed in more detail when we discuss fracture mechanics. The stresses
can be calculated as
Equivalent expressions in rectangular coordinates
are
while the displacements can be calculated by
integrating the strains, with the result
Note that this displacement
field is valid for plane strain deformation only.
Observe that the stress intensity factor has the
bizarre units of .
 The elastic constants for the solid and its mass density
The elastic constants for the solid and its mass density ![]() Displacementstrain relation or
Displacementstrain relation or
![]() The Stressstrain-temperature
relation
The Stressstrain-temperature
relation ![]() Equilibrium
Equation or
Equilibrium
Equation or ![]() Traction
boundary conditions on parts of the boundary where tractions are
known.
Traction
boundary conditions on parts of the boundary where tractions are
known.![]() Displacement
boundary conditions on
parts of the boundary where displacements are known.
Displacement
boundary conditions on
parts of the boundary where displacements are known.




 A representative spherically
symmetric problem is illustrated in the picture. We consider a hollow, spherical solid, which
is subjected to spherically symmetric loading (i.e. internal body forces, as
well as tractions or displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be
spherically symmetric (a function of R
only).
A representative spherically
symmetric problem is illustrated in the picture. We consider a hollow, spherical solid, which
is subjected to spherically symmetric loading (i.e. internal body forces, as
well as tractions or displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be
spherically symmetric (a function of R
only).![]() Position Vector
Position Vector
![]() Displacement
vector
Displacement
vector ![]() Body
force vector
Body
force vector ![]() Strain Displacement Relations
Strain Displacement Relations ![]() StressStrain relations
StressStrain relations![]() Equilibrium Equations
Equilibrium Equations![]() Boundary Conditions
Boundary Conditions Example
1: Pressurized hollow sphere
Example
1: Pressurized hollow sphere![]() No body forces act on the sphere
No body forces act on the sphere![]() The sphere has uniform temperature
The sphere has uniform temperature![]() The inner surface R=a is subjected to pressure
The inner surface R=a is subjected to pressure ![]() The outer surface R=b is subjected to pressure
The outer surface R=b is subjected to pressure  Example
2: Gravitating sphere
Example
2: Gravitating sphere![]() A body force per unit mass, where g is the acceleration due to
gravity at the surface of the sphere
A body force per unit mass, where g is the acceleration due to
gravity at the surface of the sphere![]() A uniform temperature distribution
A uniform temperature distribution![]() A traction free surface at R=a
A traction free surface at R=a Example 3: Sphere with steady state heat flow
Example 3: Sphere with steady state heat flow![]() No body force acts on the sphere
No body force acts on the sphere![]() The temperature distribution in the sphere is
The temperature distribution in the sphere is![]() The surfaces at R=a and R=b are traction free.
The surfaces at R=a and R=b are traction free. Two examples of axially symmetric
problems are illustrated in the picture.
In both cases the solid is a circular cylinder, which is subjected to
axially symmetric loading (i.e. internal body forces, as well as tractions or
displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be axially
symmetric (a function of r
only). Finally, the solid can spin with
steady angular velocity about the axis.
Two examples of axially symmetric
problems are illustrated in the picture.
In both cases the solid is a circular cylinder, which is subjected to
axially symmetric loading (i.e. internal body forces, as well as tractions or
displacements applied to the surface, are independent of and ,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be axially
symmetric (a function of r
only). Finally, the solid can spin with
steady angular velocity about the axis. The state of stress and strain in the
solid depends on the loads applied to the ends of the cylinder. Specifically
The state of stress and strain in the
solid depends on the loads applied to the ends of the cylinder. Specifically![]() If the cylinder is completely prevented from
stretching in the direction a state of plane strain exists in the solid.
This is an exact solution to the 3D equations of elasticity, is valid
for a cylinder with any length, and is accurate everywhere in the cylinder.
If the cylinder is completely prevented from
stretching in the direction a state of plane strain exists in the solid.
This is an exact solution to the 3D equations of elasticity, is valid
for a cylinder with any length, and is accurate everywhere in the cylinder.![]() If the top and bottom surface of the short
plate-like cylinder are free of traction, a state of plane stress exists in the solid.
This is an approximate solution to the 3D equations of elasticity, and
is accurate only if the cylinder’s length is much less than its diameter.
If the top and bottom surface of the short
plate-like cylinder are free of traction, a state of plane stress exists in the solid.
This is an approximate solution to the 3D equations of elasticity, and
is accurate only if the cylinder’s length is much less than its diameter. ![]() If the top and bottom ends of the long cylinder are subjected to a
prescribed force (or the ends are free of force) a state of generalized plane strain exists in the
cylinder. This is an approximate
solution, which is accurate only away from the ends of a long cylinder. As a rule of thumb, the solution is
applicable approximately three cylinder radii away from the ends.
If the top and bottom ends of the long cylinder are subjected to a
prescribed force (or the ends are free of force) a state of generalized plane strain exists in the
cylinder. This is an approximate
solution, which is accurate only away from the ends of a long cylinder. As a rule of thumb, the solution is
applicable approximately three cylinder radii away from the ends. ![]() Position
Vector
Position
Vector ![]() Displacement vector
Displacement vector ![]() Body force vector
Body force vector ![]() Acceleration vector
Acceleration vector ![]() Strain Displacement Relations
Strain Displacement Relations ![]() StressStrain relations
(plane strain and generalized plane strain)
StressStrain relations
(plane strain and generalized plane strain)![]() StressStrain relations
(plane stress)
StressStrain relations
(plane stress)![]() Equation of motion
Equation of motion![]() Boundary Conditions
Boundary Conditions
![]() No body forces act on the cylinder
No body forces act on the cylinder![]() The cylinder has zero angular velocity
The cylinder has zero angular velocity![]() The sphere has uniform temperature
The sphere has uniform temperature![]() The inner surface r=a is subjected to pressure
The inner surface r=a is subjected to pressure ![]() The outer surface r=b is subjected to pressure
The outer surface r=b is subjected to pressure ![]() For the plane strain solution, the cylinder
does not stretch parallel to its axis.
For the generalized plane strain solution, the ends of the cylinder are
subjected to an axial force as shown.
In particular, for a closed ended
cylinder the axial force exerted by the pressure inside the cylinder acting on
the closed ends is
For the plane strain solution, the cylinder
does not stretch parallel to its axis.
For the generalized plane strain solution, the ends of the cylinder are
subjected to an axial force as shown.
In particular, for a closed ended
cylinder the axial force exerted by the pressure inside the cylinder acting on
the closed ends is  Example 2: Spinning circular plate
Example 2: Spinning circular plate![]() No body forces act on the disk
No body forces act on the disk![]() The disk has constant angular velocity
The disk has constant angular velocity![]() The disk has uniform temperature
The disk has uniform temperature![]() The outer surface r=a and the top and bottom faces of the disk are free of traction.
The outer surface r=a and the top and bottom faces of the disk are free of traction.![]() The disk is sufficiently thin to ensure a
state of plane stress in the disk.
The disk is sufficiently thin to ensure a
state of plane stress in the disk.
![]() No body forces act on the solids
No body forces act on the solids![]() The angular velocity is zero
The angular velocity is zero![]() The cylinders have uniform temperature
The cylinders have uniform temperature![]() The shaft slides freely inside the bushing
The shaft slides freely inside the bushing![]() The ends of the cylinder are free of force.
The ends of the cylinder are free of force.![]() Both the shaft and cylinder have the same
Young’s modulus E and Poisson’s ratio
Both the shaft and cylinder have the same
Young’s modulus E and Poisson’s ratio
![]() The cylinder and shaft are sufficiently long
to ensure that a state of generalized plane strain can be developed in each
solid.
The cylinder and shaft are sufficiently long
to ensure that a state of generalized plane strain can be developed in each
solid. In this section we outline a general
technique for solving 2D static linear elasticity problems. The technique is known as the `Airy Stress
Function’ method.
In this section we outline a general
technique for solving 2D static linear elasticity problems. The technique is known as the `Airy Stress
Function’ method.![]() The Airy stress function is applicable only to
isotropic solids. We will assume that the solid has Young’s modulus E, Poisson’s ratio and mass density
The Airy stress function is applicable only to
isotropic solids. We will assume that the solid has Young’s modulus E, Poisson’s ratio and mass density ![]() The Airy Stress function can only be used if the body
force has a special form. Specifically,
the requirement is
The Airy Stress function can only be used if the body
force has a special form. Specifically,
the requirement is![]() The
Airy Stress Function approach works best for problems where a solid is
subjected to prescribed tractions on its boundary, rather than prescribed
displacements. Specifically, we will
assume that the solid is loaded by boundary tractions .
The
Airy Stress Function approach works best for problems where a solid is
subjected to prescribed tractions on its boundary, rather than prescribed
displacements. Specifically, we will
assume that the solid is loaded by boundary tractions .![]() must satisfy the
following traction boundary conditions on the surface of the solid
must satisfy the
following traction boundary conditions on the surface of the solid![]() , the stress field within the region of interest can be
calculated from the formulas
, the stress field within the region of interest can be
calculated from the formulas![]() than it is to solve
for stress directly, this is still not a trivial exercise. Usually, one guesses a suitable form for
than it is to solve
for stress directly, this is still not a trivial exercise. Usually, one guesses a suitable form for ![]() , as illustrated below.
This may seem highly unsatisfactory, but remember that we are
essentially integrating a system of PDEs.
The general procedure to evaluate any integral is to guess a solution,
differentiate it, and see if the guess was correct.
, as illustrated below.
This may seem highly unsatisfactory, but remember that we are
essentially integrating a system of PDEs.
The general procedure to evaluate any integral is to guess a solution,
differentiate it, and see if the guess was correct. ![]() Displacementstrain relation
Displacementstrain relation ![]() Stressstrain relation
Stressstrain relation ![]() Equilibrium
Equation
Equilibrium
Equation ![]() to see that
to see that![]() . To ensure that the
other two equations are satisfied, we first compute the strains using the
elastic stress-strain equations. Recall
that
. To ensure that the
other two equations are satisfied, we first compute the strains using the
elastic stress-strain equations. Recall
that![]() and rearrange to see
that
and rearrange to see
that
 Consider a cantilever beam, with length L, height 2a and out-of-plane thickness b,
as shown in the figure. The beam is made from an isotropic linear elastic solid
with Young’s modulus and Poisson ratio .
The top and bottom of the beam are traction free, the left hand end is
subjected to a resultant force P, and
the right hand end is clamped. Assume
that b<<a, so that a state of
plane stress is developed in the beam. An approximate solution to the stress in
the beam can be calculated from the Airy function
Consider a cantilever beam, with length L, height 2a and out-of-plane thickness b,
as shown in the figure. The beam is made from an isotropic linear elastic solid
with Young’s modulus and Poisson ratio .
The top and bottom of the beam are traction free, the left hand end is
subjected to a resultant force P, and
the right hand end is clamped. Assume
that b<<a, so that a state of
plane stress is developed in the beam. An approximate solution to the stress in
the beam can be calculated from the Airy function
 The formulas in the preceding section yield
The formulas in the preceding section yield Example
4: Arbitrary pressure acting on a flat surface
Example
4: Arbitrary pressure acting on a flat surface For the particular case of a uniform pressure, the
integrals can be evaluated to show that
For the particular case of a uniform pressure, the
integrals can be evaluated to show that Consider an infinite solid, which contains a
semi-infinite crack on the (x1,x3) plane.
Suppose that the solid deforms in plane strain and is subjected to bounded
stress at infinity. The stress field
near the tip of the crack can be derived from the Airy function
Consider an infinite solid, which contains a
semi-infinite crack on the (x1,x3) plane.
Suppose that the solid deforms in plane strain and is subjected to bounded
stress at infinity. The stress field
near the tip of the crack can be derived from the Airy function