Chapter 7

 

Stress-Strain relations for linear elastic materials

 

You are probably familiar with the behavior of a linear elastic material from introductory materials courses.

7.1 Isotropic, linear elastic material behavior

 

If you conduct a uniaxial tensile test on almost any material, and keep the stress levels sufficiently low, you will observe the following behavior:

 The specimen deforms reversibly:  If you remove the loads, the solid returns to its original shape.

 The strain in the specimen depends only on the stress applied to it $–$ it doesn’t depend on the rate of loading, or the history of loading.

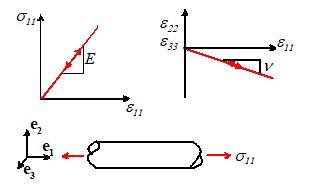
 For most materials, the stress is a linear function of strain, as shown in the picture above.  Because the strains are small, this is true whatever stress measure is adopted (Cauchy stress or nominal stress), and is true whatever strain measure is adopted (Lagrange strain or infinitesimal strain).

 For most, but not all, materials, the material has no characteristic orientation.  Thus, if you cut a tensile specimen out of a block of material, as shown in the figure, the the stress$—$strain curve will be independent of the orientation of the specimen relative to the block of material.  Such materials are said to be isotropic.

 If you heat a specimen of the material, increasing its temperature uniformly, it will generally change its shape slightly.  If the material is isotropic (no preferred material orientation) and homogeneous, then the specimen will simply increase in size, without shape change.

 

 

7.2 Stress$—$strain relations for isotropic, linear elastic materials. Young’s Modulus, Poissons ratio and the Thermal Expansion Coefficient.

 

Before writing down stress$—$strain relations, we need to decide what strain and stress measures we want to use.  Because the model only works for small shape changes

 Deformation is characterized using the infinitesimal strain tensor ${\epsilon }_{ij}=\left(\partial u_i/\partial x_j+\partial u_j/\partial x_i\right)/2$ defined in Section 4.6.  This is convenient for calculations, but has the disadvantage that linear elastic constitutive equations can only be used if the solid experiences small rotations, as well as small shape changes. 

 All stress measures are taken to be equal.  We can use the Cauchy stress ${\sigma }_{ij}$ as the stress measure.

 

You probably already know the stress$—$strain relations for an isotropic, linear elastic solid.  They are repeated below for convenience.

$\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{33}\\ 2{\epsilon }_{23}\\ 2{\epsilon }_{13}\\ 2{\epsilon }_{12}\end{array}\right]=\frac{1}{E}\left[\begin{array}{cccccc}1& -\nu & -\nu & 0& 0& 0\\ -\nu & 1& -\nu & 0& 0& 0\\ -\nu & -\nu & 1& 0& 0& 0\\ 0& 0& 0& 2\left(1+\nu \right)& 0& 0\\ 0& 0& 0& 0& 2\left(1+\nu \right)& 0\\ 0& 0& 0& 0& 0& 2\left(1+\nu \right)\end{array}\right]\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\sigma }_{23}\\ {\sigma }_{13}\\ {\sigma }_{12}\end{array}\right]+\alpha \Delta T\left[\begin{array}{c}1\\ 1\\ 1\\ 0\\ 0\\ 0\end{array}\right]$

Here, E and $\nu$ are Young’s modulus and Poisson’s ratio, $\alpha$ is the coefficient of thermal expansion, and $\Delta T$ is the increase in temperature of the solid.  The remaining relations can be deduced from the fact that both ${\sigma }_{ij}$ and ${\epsilon }_{ij}$ are symmetric. 

 

The inverse relationship can be expressed as

$\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\sigma }_{23}\\ {\sigma }_{13}\\ {\sigma }_{12}\end{array}\right]=\frac{E}{(1+\nu )(1-2\nu )}\left[\begin{array}{cccccc}1-\nu & \nu & \nu & 0& 0& 0\\ \nu & 1-\nu & \nu & 0& 0& 0\\ \nu & \nu & 1-\nu & 0& 0& 0\\ 0& 0& 0& \frac{\left(1-2\nu \right)}{2}& 0& 0\\ 0& 0& 0& 0& \frac{\left(1-2\nu \right)}{2}& 0\\ 0& 0& 0& 0& 0& \frac{\left(1-2\nu \right)}{2}\end{array}\right]\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{33}\\ 2{\epsilon }_{23}\\ 2{\epsilon }_{13}\\ 2{\epsilon }_{12}\end{array}\right]-\frac{E\alpha \Delta T}{1-2\nu }\left[\begin{array}{c}1\\ 1\\ 1\\ 0\\ 0\\ 0\end{array}\right]$

 

HEALTH WARNING: Note the factor of 2 in the strain vector.  Most texts, and most FEM codes use this factor of two, but not all.  In addition, shear strains and stresses are often listed in a different order in the strain and stress vectors.  For isotropic materials this makes no difference, but you need to be careful when listing material constants for anisotropic materials (see below).

 

We can write this expression in a much more convenient form using index notation.  Verify for yourself that the matrix expression above is equivalent to

${\epsilon }_{ij}=\frac{1+\nu }{E}{\sigma }_{ij}-\frac{\nu }{E}{\sigma }_{kk}{\delta }_{ij}+\alpha \Delta T{\delta }_{ij}$

 

The inverse relation is

${\sigma }_{ij}=\frac{E}{1+\nu }\left\{{\epsilon }_{ij}+\frac{\nu }{1-2\nu }{\epsilon }_{kk}{\delta }_{ij}\right\}-\frac{E\alpha \Delta T}{1-2\nu }{\delta }_{ij}$

 

The stress-strain relations are often expressed using the elastic modulus tensor $C_{ijkl}$ or the elastic compliance tensor $S_{ijkl}$ as

${\sigma }_{ij}=C_{ijkl}\left({\epsilon }_{kl}-\alpha \Delta T{\delta }_{kl}\right){\epsilon }_{ij}=S_{ijkl}{\sigma }_{kl}+\alpha \Delta T{\delta }_{ij}$

In terms of elastic constants, $C_{ijkl}$ and $S_{ijkl}$ are

$\begin{array}{l}{C}_{ijkl}=\frac{E}{2\left(1+\nu \right)}\left({\delta }_{il}{\delta }_{jk}+{\delta }_{ik}{\delta }_{jl}\right)+\frac{E\nu }{\left(1+\nu \right)\left(1-2\nu \right)}{\delta }_{ij}{\delta }_{kl}\\ S_{ijkl}=\frac{1+\nu }{2E}\left({\delta }_{il}{\delta }_{jk}+{\delta }_{ik}{\delta }_{jl}\right)-\frac{\nu }{E}{\delta }_{ij}{\delta }_{kl}\end{array}$

 

 

 

7.3 Reduced stress-strain equations for plane deformation of isotropic solids

 

For plane strain or plane stress deformations, some strain or stress components are always zero (by definition) so the stress-strain laws can be simplified. 

 

 

 For a plane strain deformation ${\epsilon }_{33}={\epsilon }_{23}={\epsilon }_{13}=0$.  The stress strain laws are therefore

$\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ 2{\epsilon }_{12}\end{array}\right]=\frac{(1+\nu )}{E}\left[\begin{array}{ccc}1-\nu & -\nu & 0\\ -\nu & 1-\nu & 0\\ 0& 0& 2\end{array}\right]\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\end{array}\right]+\left(1+\nu \right)\alpha \Delta T\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]$

$\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\end{array}\right]=\frac{E}{(1+\nu )(1-2\nu )}\left[\begin{array}{ccc}1-\nu & \nu & 0\\ \nu & 1-\nu & 0\\ 0& 0& \frac{1-2\nu }{2}\end{array}\right]\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ 2{\epsilon }_{12}\end{array}\right]-\frac{E\alpha \Delta T}{1-2\nu }\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]$

${\sigma }_{33}=\frac{E\nu \left({\epsilon }_{11}+{\epsilon }_{22}\right)}{\left(1-2\nu \right)\left(1+\nu \right)}+\frac{E\alpha \Delta T}{1-2\nu },{\sigma }_{13}={\sigma }_{23}=0$

In index notation

${\epsilon }_{\alpha \beta }=\frac{1+\nu }{E}\left\{{\sigma }_{\alpha \beta }-\nu {\sigma }_{\gamma \gamma }{\delta }_{\alpha \beta }\right\}+\left(1+\nu \right)\alpha \Delta T{\delta }_{\alpha \beta }{\sigma }_{\alpha \beta }=\frac{E}{1+\nu }\left\{{\epsilon }_{\alpha \beta }+\frac{\nu }{1-2\nu }{\epsilon }_{\gamma \gamma }{\delta }_{\alpha \beta }\right\}-\frac{E\alpha \Delta T}{1-2\nu }{\delta }_{\alpha \beta }$

where Greek subscripts $\alpha ,\beta$ can have values 1 or 2.

 

 For a plane stress deformation ${\sigma }_{33}={\sigma }_{23}={\sigma }_{13}=0$

 

$\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ 2{\epsilon }_{12}\end{array}\right]=\frac{1}{E}\left[\begin{array}{ccc}1& -\nu & 0\\ -\nu & 1& 0\\ 0& 0& 2(1+\nu )\end{array}\right]\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\end{array}\right]+\alpha \Delta T\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]$

$\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\end{array}\right]=\frac{E}{(1-{\nu }^2)}\left[\begin{array}{ccc}1& \nu & 0\\ \nu & 1& 0\\ 0& 0& (1-\nu )/2\end{array}\right]\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ 2{\epsilon }_{12}\end{array}\right]-\frac{E\alpha \Delta T}{\left(1-\nu \right)}\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]$

${\epsilon }_{33}=-\frac{\nu }{E}\left({\sigma }_{11}+{\sigma }_{22}\right)+\alpha \Delta T$

${\epsilon }_{\alpha \beta }=\frac{1+\nu }{E}\left({\sigma }_{\alpha \beta }-\frac{\nu }{1+\nu }{\sigma }_{\gamma \gamma }{\delta }_{\alpha \beta }\right)+\alpha \Delta T{\delta }_{\alpha \beta }{\sigma }_{\alpha \beta }=\frac{E}{1+\nu }\left\{{\epsilon }_{\alpha \beta }+\frac{\nu }{1-\nu }{\epsilon }_{\gamma \gamma }{\delta }_{\alpha \beta }\right\}-\frac{E\alpha \Delta T}{1-\nu }{\delta }_{\alpha \beta }$

 

 

 

7.4 Representative values for density, and elastic constants of isotropic solids

 

Most of the data in the table below were taken from the excellent introductory text `Engineering Materials,’ by M.F. Ashby and D.R.H. Jones, Pergamon Press.  The remainder are from random web pages…

 

Note the units $–$ values of E are given in $GN/m^2$; the G stands for Giga, and is short for ${10}^9$.  The units for density are in $Mg{m}^{-3}$ - that’s Mega grams.  One mega gram is 1000 kg.

 

 

 

 

 

 

7.5 Other Elastic Constants $–$ bulk, shear and Lame modulus.

 

Young’s modulus and Poisson’s ratio are the most common properties used to characterize elastic solids, but other measures are also used.  For example, we define the shear modulus,  bulk modulus and Lame modulus of an elastic solid as follows:

$\begin{array}{l}\text{Bulk Modulus }K=\frac{E}{3\left(1-2\nu \right)}\\ \text{Shear Modulus }\mu \text{=}\frac{E}{2\left(1+\nu \right)}\\ \text{Lame Modulus }\lambda =\frac{\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}\end{array}$

 

A nice table relating all the possible combinations of moduli to all other possible combinations is given below.  Enjoy!

 

 

 

 

 

 

 

7.6 Physical Interpretation of elastic constants for isotropic solids

 

It is important to have a feel for the physical significance of the two elastic constants E and $\nu$.

 

  Young’s modulus E is the slope of the stress$—$strain curve in uniaxial tension.  It has dimensions of stress ( $N/m^2$ ) and is usually large $–$ for steel, $E=210\times {10}^9{\text{N/m}}^{\text{2}}$. You can think of E as a measure of the stiffness of the solid. The larger the value of E, the stiffer the solid.  For a stable material, E>0.

 

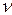 Poisson’s ratio  is the ratio of lateral to longitudinal strain in uniaxial tensile stress. It is dimensionless and typically ranges from 0.2$—$0.49, and is around 0.3 for most metals.  For a stable material, $-1<\nu <0.5$. It is a measure of the compressibility of the solid.  If $\nu =0.5$, the solid is incompressible $–$ its volume remains constant, no matter how it is deformed.  If $\nu =0$, then stretching a specimen causes no lateral contraction.  Some bizarre materials have $\nu <0$ --  if you stretch a round bar of such a material, the bar increases in diameter!!

 

 Thermal expansion coefficient quantifies the change in volume of a material if it is heated in the absence of stress.  It has dimensions of (degrees Kelvin)^-1 and is usually very small.  For steel, $\alpha \approx 6-10\times {10}^{-6}{\text{K}}^{\text{-1}}$

 

 The bulk modulus quantifies the resistance of the solid to volume changes.  It has a large value (usually bigger than E).

 

 The shear modulus quantifies its resistance to volume preserving shear deformations.  Its value is usually somewhat smaller than E. 

 

 

 

7.7 Strain Energy Density for Isotropic Solids

 

Note the following observations

 If you deform a block of material, you do work on it (or, in some cases, it may do work on you…) 

 In an elastic material, the work done during loading is stored as recoverable strain energy in the solid.  If you unload the material, the specimen does work on you, and when it reaches its initial configuration you come out even.

 The work done to deform a specimen depends only on the state of strain at the end of the test.  It is independent of the history of loading. 

 

Based on these observations, we define the strain energy density of a solid as the work done per unit volume to deform a material from a stress free reference state to a loaded state.

 

To write down an expression for the strain energy density, it is convenient to separate the strain into two parts

${\epsilon }_{ij}={\epsilon }_{ij}^e+{\epsilon }_{ij}^T$

where, for an isotropic solid,

${\epsilon }_{ij}^T=\alpha \Delta T{\delta }_{ij}$

represents the strain due to thermal expansion (known as thermal strain), and

${\epsilon }_{ij}^e=\frac{1+\nu }{E}{\sigma }_{ij}-\frac{\nu }{E}{\sigma }_{kk}{\delta }_{ij}$

is the strain due to mechanical loading (known as elastic strain).

 

Work is done on the specimen only during mechanical loading.  It is straightforward to show that the strain energy density is

$U=\frac{1}{2}{\sigma }_{ij}{\epsilon }_{ij}^e$

You can also re-write this as

$\begin{array}{l}U=\frac{1+\nu }{2E}{\sigma }_{ij}{\sigma }_{ij}-\frac{\nu }{2E}{\sigma }_{kk}{\sigma }_{jj}\\ U=\frac{E}{2\left(1+\nu \right)}{\epsilon }_{ij}^e{\epsilon }_{ij}^e+\frac{E\nu }{2\left(1+\nu \right)\left(1-2\nu \right)}{\epsilon }_{jj}^e{\epsilon }_{kk}^e\end{array}$

Observe that

${\epsilon }_{ij}^e=\frac{\partial U}{\partial {\sigma }_{ij}}{\sigma }_{ij}=\frac{\partial U}{\partial {\epsilon }_{ij}^e}$