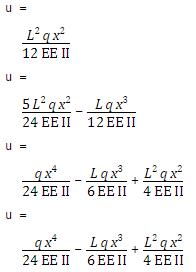Chapter 9
Energy Methods for Linear Elastic Solids
You
may recall that energy methods can often be used to simplify complex
problems. For example, to find the
equilibrium configuration of a discrete system, you would begin by identifying
a suitable set of generalize coordinates ,
and then express the potential energy in terms of these: . The equilibrium values of the generalized
coordinates could then be determined from the condition that the potential
energy is stationary at equilibrium: this gives a set of equations that could be solved for .
In
this section, we will develop an analogous procedure for solving boundary value
problems in linear elasticity. Our generalized
coordinates will be the displacement field . We will find an expression for the potential
energy of an elastic solid in terms of ,
and then show that the potential energy is stationary if the solid is in equilibrium. We will find, further, that the potential
energy is not only stationary, but is always a minimum, implying that
equilibrium configurations in linear elasticity problems are always stable.
(This is because the approximations made in setting up the equations of
linear elasticity preclude any possibility of buckling). This principle will be referred to as the Principle of Minimum Potential Energy.
The
main application of the principle is to generate approximate solutions to
linear elastic boundary value problems.
Indeed, the principle will form the basis of the Finite Element Method
in linear elasticity.
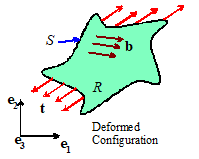 In the following, we consider a generic static
boundary value problem in linear elasticity, as shown in the picture.
In the following, we consider a generic static
boundary value problem in linear elasticity, as shown in the picture.
As always, we assume that
we are given:
1. The shape of the solid in its unloaded condition
2. The initial stress field in the solid (we will take
this to be zero)
3. The elastic constants for the solid and its mass density
4. The thermal expansion coefficients for the solid, and
temperature change from the initial configuration
5. A body force distribution (per unit mass) acting on the solid
6. Boundary conditions, specifying displacements on a portion or tractions on a portion of the boundary of R
9.1 Kinematically Admissible Displacement Fields
A
‘kinematically admissible displacement field’ is any displacement field with the following
properties:
1.
is continuous everywhere within the solid
2. is differentiable everywhere within the solid,
so that a strain field may be computed as
3. satisfies boundary conditions anywhere that
displacements are prescribed, i.e. on the portion on the
boundary.
Note the v is not
necessarily the actual displacement
in the solid it is just an arbitrary displacement field
which satisfies any displacement boundary conditions. You can think of it as a possible displacement field that the solid could adopt. Out of all
these possible displacement fields, it will actually select the one that
minimizes the potential energy.
The kinematically admissible displacement field can also be
thought of as a system of generalized coordinates in the context of analytical
mechanics. Recall that, to use a set of
generalized coordinates in Lagranges equations, you must make sure that the
system of coordinates satisfies all the constraints. Similarly, to be admissible, our displacement
field must satisfy constraints on the boundary.
9.2 Definition of Potential Energy of
an Elastic Solid
Next, we will define the potential energy of a solid. The definition may look a bit strange,
because it seems to give different values for potential energy depending on how
the solid is loaded. This is true. But who cares, as long as the definition is
useful?
For any
kinematically admissible displacement field v, the potential energy is
where
is
the strain energy density associated with the kinematically admissible displacement
field. You can interpret the three terms in the formula for V as the strain energy stored inside the
solid; the work done by body forces; and the work done by surface tractions.
For the particular case of an isotropic material, with ,
we see that
9.3 The principle of stationary and minimum potential
energy.
Let
v be any kinematically admissible
displacement field. Let u be the actual displacement field i.e. the one that satisfies the equilibrium
equations within the solid as well as all the boundary conditions. We will show the following:
1.
V(v) is stationary (i.e. a local
minimum, maximum or inflexion point) for v=u.
2.
V(v) is a global minimum for v=u.
As
a preliminary step, recall that the actual displacement field satisfies the
following equations
Next, re-write the
kinematically admissible displacement field in terms of u as
where
is the difference between the kinematically
admissible field and the correct equilibrium field. Observe that
i.e.
the difference between the kinematically admissible field and the actual field
is zero wherever displacements are prescribed.
Now,
note that can be expressed in terms of and as
where
To see this, simply
substitute into the definition of the potential energy
Multiply everything out and
use the condition that to get the result stated.
Now,
to show that is stationary at v=u, we need to show that . This means that, if we add any small change to the actual displacement field u, the change in potential energy will
be zero, to first order in .
To show this, note that
Next, note that
where
we have used the fact that (angular momentum balance). Rewrite this as
Substitute back into the
expression for  and rearrange to see
that
and rearrange to see
that
Now, recall the equations
of equilibrium
so
that the second term vanishes. Apply the
divergence theorem to express the first integral as a surface integral
Recall that ,
and note that
because
either tractions or displacements (but not both) must be prescribed on every
point on the boundary.
Therefore
Finally, recall that
and substitute back into
the expression for to see that
This proves that V(v)
is stationary at v=u, as stated.
Finally,
we wish to show that V(v) is a minimum at v=u. This is easy. Note that we have proved that
Note that
is the strain energy
density associated with a strain . Strain energy density must always be positive
or zero, so that
9.4 Useful Formulas for Potential Energy
Besides 3D elastic solids,
we often use energy methods to analyze solids with special shapes, such as
strings, beams, membranes and plates.
These will be discussed in more detail in Section 11, but it is helpful
to list formulas for the potential energies of these special solids here, so we
can use them in example problems.
|
1-D Axially loaded bar
|
|
|
1-D Tensioned Cable
|
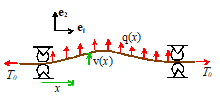
|
|
1-D Euler-Bernoulli Beam
|
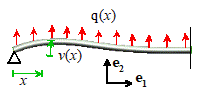
|
|
2D Biaxially Stretched Membrane
|
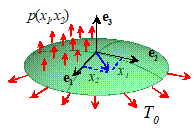
|
|
2D Kirchhoff Plate
|
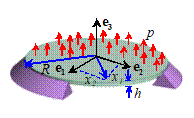
|
9.5 Uniaxial compression of a cylinder solved by
energy methods
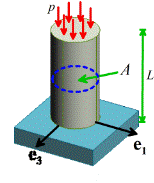 Consider a cylindrical bar subjected to a uniform
pressure p on one end, and supported on
a rigid, frictionless base. Neglect
temperature changes. Determine the
displacement field in the bar.
Consider a cylindrical bar subjected to a uniform
pressure p on one end, and supported on
a rigid, frictionless base. Neglect
temperature changes. Determine the
displacement field in the bar.
We will
solve this problem using energy methods.
We will guess a displacement field of the form
This satisfies the boundary conditions on the bottom face of
the cylinder, so it is a kinematically admissible displacement field. The coefficients are to be determined, by minimizing the
potential energy. The strains follow as
with all
other strain components zero. The strain
energy density is
The boundary conditions are
1.
On the bottom of
the cylinder
2.
On the sides of
the cylinder,
3.
On the top of the
cylinder
Substitute into the
expression for strain energy density to see that
Now, the actual
displacement field minimizes V. This requires
Evaluate the derivatives to
see that
It
is easy to solve these equations to see that
This
is, of course, the exact solution, which is reassuring. Notice that we never had to calculate
stresses or worry about equilibrium the variational principle takes care of all
that for us.
Let
us solve the same problem, but this time with displacement boundary conditions on the top of the cylinder.
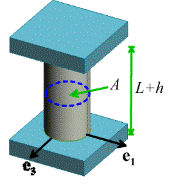 The cylinder has unstretched length L and is stretched between frictionless
grips to length L+h. This time, the kinematically admissible displacement
field must satisfy boundary conditions on both top and bottom surface of the
cylinder. Therefore, we choose
The cylinder has unstretched length L and is stretched between frictionless
grips to length L+h. This time, the kinematically admissible displacement
field must satisfy boundary conditions on both top and bottom surface of the
cylinder. Therefore, we choose
Proceeding
as before, we now find that the potential energy is
Note
that this time there is no contribution to the potential energy from the
tractions on the top of the cylinder, because now the displacement is prescribed there, instead of the pressure. Minimizing the potential energy as before
Solve these equations to
conclude that
Again, this is the exact
solution.
9.6 Energy
methods for calculating stiffness
 Energy methods can also be used to obtain an upper
bound to the stiffness of a structure or a component.
Energy methods can also be used to obtain an upper
bound to the stiffness of a structure or a component.
Begin
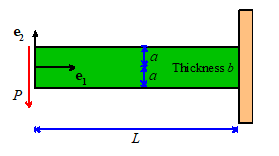
by reviewing the meaning of stiffness of an elastic solid. A spring is an example of an elastic
solid. Recall that if you apply a force P to a spring, it deflects by an amount ,
in proportion to P. The stiffness k is defined so that
If
you apply a load P to any elastic structure (except one which
contains two or more contacting surfaces), the point where you apply the load
will deflect by a distance that is proportional to the applied load. For example, for a cantilever beam, the end
deflection is
The stiffness of the beam
is therefore
 To get an upper bound to the stiffness of a structure,
one can merely guess its deformed shape, then apply the principle of minimum
potential energy.
To get an upper bound to the stiffness of a structure,
one can merely guess its deformed shape, then apply the principle of minimum
potential energy.
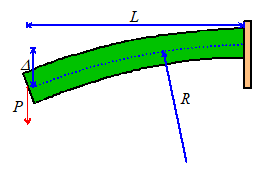
For
example, for the beam problem, we might guess that the beam deforms into a
circular shape, with unknown radius R.
The
deflection at the end of the beam is approximately
From the
preceding section, we know that the potential energy of a beam is
Here, ,
but we need to account for the potential energy of the load P.
Recall that the potential energy of a constant force is .
Recall also that .
Thus
Choose R to minimize the potential energy
so that
For comparison, the exact
solution is
9.7 Rayleigh-Ritz Method for
Calculating Approximate Static Solutions for Elastic Solids
The
so-called Rayleigh-Ritz method is a formal procedure for obtaining approximate
solutions to boundary value problems in elasticity. It is best illustrated by working through a
series of examples, while summarizing the general procedure along the way.
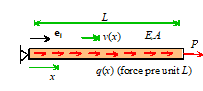
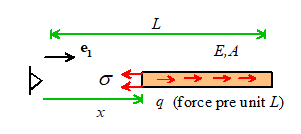
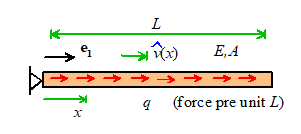 Example 1: The
bar shown in the figure is loaded by uniform body forces q per unit length. Estimate
the displacement in the bar.
Example 1: The
bar shown in the figure is loaded by uniform body forces q per unit length. Estimate
the displacement in the bar.
1. Start by guessing an approximate
solution that can be progressively improved by adding additional terms. It is helpful to choose a form for the
solution that will (with sufficient terms) interpolate any differentiable
function exactly in the limit of an infinite number of terms. We often use functions such as
where is some
a set of basis functions, - examples include
We can add more and more terms to the polynomial to
progressively improve the approximation.
For our present example a polynomial is a good choice, so we choose
2. To be a kinematically admissible
displacement field, the interpolated approximation must satisfy any boundary
conditions. Here, we require ,
which shows that . More
generally, the boundary conditions yield a
set of linear equatinos for the coefficients .
These can be used to eliminate some subset of the unknowns. It doesn’t matter which ones you eliminate,
but it is essential to do the elimination before calculating the potential
energy.
3. Next, we calculate the potential
energy. As an example, let’s choose just one nonzero
term . The formula for potential energy gives
4. Now we minimize the potential energy
with respect to all the remaining coefficients in the approximation. This means the partial derivative with
respect to each coefficient in turn must be zero (because the function is
stationary). Here we just have one term
5. Solve for all the remaining
coefficients
Let’s
repeat the procedure but use two terms in the expansion: . We can have MATLAB do all the necessary
calculus
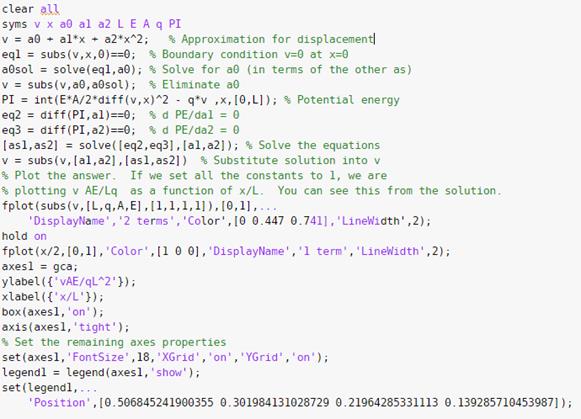
Matlab spits out the
solution
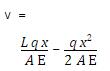
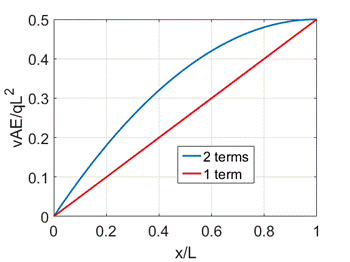
The solutions with one and
two terms are shown below.
 To wrap up this discussion, let’s
check and see what the exact solution is.
We can easily calculate the stress in the bar: the figure shows a free
body diagram for a section created by cutting through the bar at some arbitrary
position: this shows that
To wrap up this discussion, let’s
check and see what the exact solution is.
We can easily calculate the stress in the bar: the figure shows a free
body diagram for a section created by cutting through the bar at some arbitrary
position: this shows that
We can
then calculate the strain and integrate it to get the displacement
So the Rayleigh-Ritz solution with two terms gives the exact
solution. This is a general result:
if the exact solution can be interpolated exactly with a finite number of terms
in the approximation, the solution will always yield the exact solution once
the appropriate number of terms has been reached.
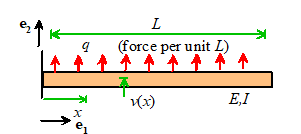 Example
2: As a second example we will use the Rayleigh-Ritz method to estimate the
solution to a cantilever beam subjected to uniform distributed loading. We can set up a general MATLAB script to do
the calculation automatically for an arbitrary number of terms: the script is
shown below.
Example
2: As a second example we will use the Rayleigh-Ritz method to estimate the
solution to a cantilever beam subjected to uniform distributed loading. We can set up a general MATLAB script to do
the calculation automatically for an arbitrary number of terms: the script is
shown below.

The succession of solutions
is shown below with 5 terms the solution is exact.
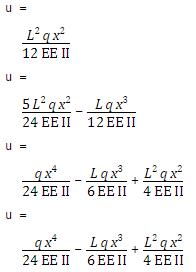
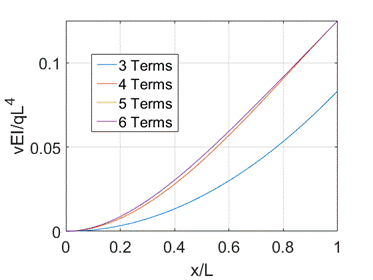
This
might give you the impression that we’ve discovered a magic procedure to solve
any elasticity problem. In a sense we
have, because the finite element method, which (with a large enough computer)
will solve most elasticity problems, is essentially a Rayleigh-Ritz
method. But the analytical approach we’ve
used in this section doesn’t always work very well, because symbolic algebra gets
very slow with a large number of unknowns.
The finite element method is much more efficient. This will be the topic of the next section.
 In the following, we consider a generic static
boundary value problem in linear elasticity, as shown in the picture.
In the following, we consider a generic static
boundary value problem in linear elasticity, as shown in the picture. ![]() and rearrange to see
that
and rearrange to see
that Consider a cylindrical bar subjected to a uniform
pressure p on one end, and supported on
a rigid, frictionless base. Neglect
temperature changes. Determine the
displacement field in the bar.
Consider a cylindrical bar subjected to a uniform
pressure p on one end, and supported on
a rigid, frictionless base. Neglect
temperature changes. Determine the
displacement field in the bar. The cylinder has unstretched length L and is stretched between frictionless
grips to length L+h. This time, the kinematically admissible displacement
field must satisfy boundary conditions on both top and bottom surface of the
cylinder. Therefore, we choose
The cylinder has unstretched length L and is stretched between frictionless
grips to length L+h. This time, the kinematically admissible displacement
field must satisfy boundary conditions on both top and bottom surface of the
cylinder. Therefore, we choose Energy methods can also be used to obtain an upper
bound to the stiffness of a structure or a component.
Energy methods can also be used to obtain an upper
bound to the stiffness of a structure or a component. To get an upper bound to the stiffness of a structure,
one can merely guess its deformed shape, then apply the principle of minimum
potential energy.
To get an upper bound to the stiffness of a structure,
one can merely guess its deformed shape, then apply the principle of minimum
potential energy.  Example 1: The
bar shown in the figure is loaded by uniform body forces q per unit length. Estimate
the displacement in the bar.
Example 1: The
bar shown in the figure is loaded by uniform body forces q per unit length. Estimate
the displacement in the bar.
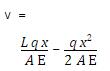

 To wrap up this discussion, let’s
check and see what the exact solution is.
We can easily calculate the stress in the bar: the figure shows a free
body diagram for a section created by cutting through the bar at some arbitrary
position: this shows that
To wrap up this discussion, let’s
check and see what the exact solution is.
We can easily calculate the stress in the bar: the figure shows a free
body diagram for a section created by cutting through the bar at some arbitrary
position: this shows that  Example
2: As a second example we will use the Rayleigh-Ritz method to estimate the
solution to a cantilever beam subjected to uniform distributed loading. We can set up a general MATLAB script to do
the calculation automatically for an arbitrary number of terms: the script is
shown below.
Example
2: As a second example we will use the Rayleigh-Ritz method to estimate the
solution to a cantilever beam subjected to uniform distributed loading. We can set up a general MATLAB script to do
the calculation automatically for an arbitrary number of terms: the script is
shown below.