Chapter 10
Implementing the Finite Element Method
for Linear Elasticity
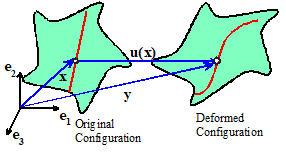
The
goal of this chapter is to provide some insight into the theory and algorithms
that are coded in a finite element program.
Here, we will implement only the simplest possible finite element code:
specifically, we will develop a finite element method to solve a 2D (plane
stress or plane strain) static boundary value problem in linear elasticity, as
shown in the picture.
We assume that we are
given:
1.
The shape of the
solid in its unloaded condition
2. Boundary conditions, specifying displacements on a portion or tractions on a portion of the boundary of R
To
simplify the problem, we will make the following assumptions
 The solid is an isotropic, linear elastic
solid with Young’s modulus E and
Poisson’s ratio ;
The solid is an isotropic, linear elastic
solid with Young’s modulus E and
Poisson’s ratio ;
 Plane
strain or plane stress deformation;
Plane
strain or plane stress deformation;
 The solid is at constant temperature (no
thermal strains);
The solid is at constant temperature (no
thermal strains);
 We will
neglect body forces.
We will
neglect body forces.
We
then wish to find a displacement field satisfying the usual field equations and
boundary conditions (see Sect 5.1.1).
The procedure is based on the principle of minimum potential energy
discussed in Section 5.7. There are four
steps:
- A finite element mesh
is constructed to interpolate the displacement field
- The strain energy in
each element is calculated in terms of the displacements of each node;
- The potential energy
of tractions acting on the solid’s boundary is added
- The displacement field
is calculated by minimizing the potential energy.
These steps are discussed in
more detail in the sections below.
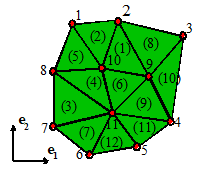 10.1 The finite element mesh
and element connectivity
10.1 The finite element mesh
and element connectivity
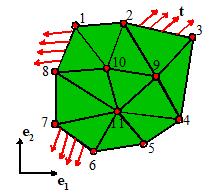
For
simplicity, we will assume that the elements are 3 noded triangles, as shown in
the picture. The nodes are numbered
1,2,3…N, while the elements are
numbered 1,2…L. Element numbers are shown in parentheses.
The position of the ath node is specified by its coordinates
The
element connectivity specifies the
node numbers attached to each element.
For example, in the picture the connectivity for element 1 is (10,9,2);
for element 2 it is (10,2,1), etc.
10.2 The global displacement vector
We
will approximate the displacement field by interpolating between values at the
nodes, as follows. Let denote the unknown displacement vector at
nodes . In a finite element code, the displacements
for a plane stress or plane strain problem are normally stored as a column
vector like the one shown below:
The
unknown displacement components will be determined by minimizing the potential
energy of the solid.
10.3 Element interpolation functions
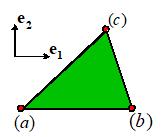
To
calculate the potential energy, we need to be able to compute the displacements
within each element. This is done by
interpolation. Consider a triangular
element, with nodes a, b, c at its
corners. Let denote the coordinates of the corners. Define the element interpolation functions
(also known as shape functions) as
follows
These shape functions are
constructed so that
 They vary
linearly with position within the element
They vary
linearly with position within the element
 Each shape
function has a value of one at one of the nodes, and is zero at the other two.
Each shape
function has a value of one at one of the nodes, and is zero at the other two.
We then write
One
can readily verify that this expression gives the correct values for at each corner of the triangle.
Of course, the shape functions
given are valid only for 3 noded triangular elements other elements have more complicated
interpolation functions.
10.4 Element strains, stresses and
strain energy density
We
can now compute the strain distribution within the element and hence determine
the strain energy density. Since we are solving a plane strain problem, the
only nonzero strains are . It is convenient to express the results in
matrix form, as follows
The
factor of 2 multiplying the shear strains in the strain vector has been
introduced for convenience. Note that,
for linear triangular elements, the matrix of shape function derivatives is constant. It depends only on the coordinates of the
corners of the element, and does not vary with position within the
element. This is not the case for most
elements.
Now,
we can compute the strain energy density within the element. Begin by computing the stresses within the
element. For plane strain deformation, have
that
For plane stress, the
result is
Recall
(see Sect 3.1.7) that the strain energy density is related to the stresses and
strains by . This can be written in matrix form as
where
Now, express these results
in terms of the nodal displacements for the element
We
can now compute the total strain energy stored within the element. Because is constant, we merely need to multiply the
strain energy density by the area of the element, which can be computed from
the coordinates of its corners as follows
Hence, the total strain
energy of the element is
10.5 The element stiffness matrix
The strain energy can be
simplified by defining the element
stiffness matrix
so that
Observe
that, because the material property matrix is symmetric, the element stiffness matrix is also symmetric. To see this, note that
10.6 The Global stiffness matrix
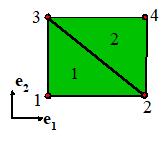 The total strain energy of the solid may be computed
by adding together the strain energy
of each element:
The total strain energy of the solid may be computed
by adding together the strain energy
of each element:
It
is more convenient to express W in
terms of the vector 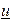 which contains all the
nodal displacements, rather than using for each element to describe the
displacements. For example, the strain
energy for the simple 2 element mesh shown is
which contains all the
nodal displacements, rather than using for each element to describe the
displacements. For example, the strain
energy for the simple 2 element mesh shown is
If we
wanted to, we could add the missing terms to each element displacement vector:
We can now collect together corresponding terms in the two
element stiffness matrices to express this as
We can therefore write
where
is known as the Global stiffness matrix. It
is the sum of all the element stiffness matrices.
Because the element stiffness matrix is
symmetric, the global stiffness matrix must also be symmetric.
To
assemble the global stiffness matrix for a plane strain or plane stress mesh
with N nodes, we use the following
procedure.
1. Note that for nodes, there will be unknown displacement components (2 at each
node). Therefore, we start by setting up
storage for a global stiffness matrix, and set each term in
the matrix to zero.
2.
Next, begin a
loop over the elements.
3.
For the current
element, assemble the element stiffness matrix
4. Add the element stiffness matrix to the global
stiffness matrix, using the following procedure. Let a,
b, c denote the numbers of the nodes on the 3 corners of the element. Let for i=1…6,
j=1…6 denote the terms in the the
element stiffness matrix. Let for n=1…2N,
m=1…2N denote the terms in the global stiffness matrix. Then,
Here,
the symbol += means that the term on the left is incremented by the term on the
right, following standard C syntax.
5.
Proceed to the next element.
10.7 Boundary loading
 We have now found a way to compute the strain energy
for a finite element
mesh. Next, we need to compute the
boundary term in the potential energy.
We have now found a way to compute the strain energy
for a finite element
mesh. Next, we need to compute the
boundary term in the potential energy.
Boundary loading will be
specified as follows:
1.
The element on which the loading acts
2.
The face of the element which is loaded
3. The traction vector t (force per unit area) that acts on the face of the element. The traction is assumed to be constant on the
face of any one element.
Now,
we compute the contribution to the potential energy due to the traction acting
on the face of one element.
For the element shown, the contribution to the potential
energy would be
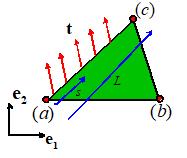 Recall that the displacements vary
linearly within a 3 noded triangle.
Therefore, we can write
Recall that the displacements vary
linearly within a 3 noded triangle.
Therefore, we can write
So, since
the tractions are uniform
Abbreviate
this as
10.8 Global force vector
The
total contribution to the potential energy due to boundary loading on all
element faces is
It is more convenient to
express this in terms of the global displacement vector
where 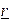 is the global residual
force vector.
is the global residual
force vector.
The global residual force
vector for a mesh with N nodes is
assembled as follows.
1. The residual force vector has length 2N (2 entries per node). Reserve storage for a vector of length 2N and initialize to zero
2.
Loop over
elements
3. Determine which face of the element is loaded. Let a,
b denote the node numbers attached to this face. Determine the residual force vector for the
element face. Let ,
i=1…4 denote the terms in the element
face residual vector. Let ,
n=1…2N denote the terms in the global
residual force vector. Then
10.9 Minimizing the Potential Energy
We have set up the
following expression for the potential energy of a finite element mesh
Now, minimize V
where we have noted that
Simplify this by noting
that is symmetric
This
is a system of 2N simultaneous linear
equations for the 2N unknown nodal
displacements. Standard computational
techniques such as Gaussian elimination, Cholesky factorization or conjugate
gradient methods may be used to solve the system of equations.
10.10 Eliminating prescribed displacements
So
far, we have seen how to calculate displacements in a finite element mesh which
is subjected to prescribed loading. What
if displacements are prescribed instead?
If
this is the case, the stiffness matrix and residual are first assembled exactly
as described in the preceding section.
They are then modified to enforce the constraint. The procedure is best illustrated using an
example. Suppose that the finite element equations after assembly have the form
To
prescribe displacements for any node, we simply replace the equation for the
appropriate degrees of freedom with the constraint. For example, to force ,
we could modify the finite element equations to
Thus, the equation for has been replaced with the constraint .
This
procedure works, but has the disadvantage that the modified stiffness matrix is
no longer symmetric. It is preferable to
modify the stiffness and residual further, to retain symmetry. To do so, we eliminate the constrained
degrees of freedom from all rows of the stiffness matrix. This is best
illustrated by example. Suppose our
modified stiffness matrix has the form
Now,
we wish to set each entry in the second column (apart from the diagonal) to
zero, so that the stiffness is symmetric.
Recall that we can add and subtract equations in the system from one
another without affecting the solution.
Therefore, to symmetrize the stiffness matrix in our example, we can
subtract appropriate multiples of the second row so as to set each entry in the
second column to zero.
10.11 Solution
The
result of Sections 10.1-10.10 is a set of simultaneous linear equations of the
form
These
can be solved for the unknown displacements using standard techniques (e.g. Gaussian
elimination or iterative techniques). An
important feature of the FEM equations is that the stiffness matrix is sparse that is to say, only a small number of entries
in the matrix are non-zero.
Consequently, special schemes are used to store and factor the
equations, which avoid having to store large numbers of zeros.
10.12
Post-processing
Once
the displacements have been computed, the strain in each element can be
computed, and so the stress distribution can be deduced. The procedure is as follows
1. For the element of interest, extract the displacement
of each node from the global displacement vector
2. Calculate the strains using the procedure in 7.2.4
3. The stresses can then be determined from the
stress-strain equations
where
is defined in 7.2.4.
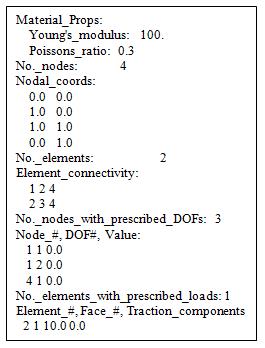
10.13 Example FEA code
A
simple MATLAB implementation of the procedure is provided in the file
FEM_conststrain_m.
 The code reads an input file. A very simple input file (with just two
elements) can be found in FEM_conststrain_input.txt. A second data file
The code reads an input file. A very simple input file (with just two
elements) can be found in FEM_conststrain_input.txt. A second data file
The
data file solves the problem illustrated in the picture. A rectangular block with Young’s modulus 100
and Poisson’s ratio 0.3 is meshed with two elements. Node 1 is pinned; node 4 is constrained
against horizontal motion, and the right hand face of element 2 is subjected to
a constant horizontal traction with magnitude 10.
The input file is shown below it should be mostly self-explanatory.
Note
that
1. Nodes are numbered sequentially thus node (1) has coordinates (0,0); node (2)
has coordinates (1,0), etc.
2. The element connectivity specifies the node numbers
attached to each element, using a counterclockwise numbering convention. It doesn’t matter which node you use for the
first one, as long as all the others are ordered in a counterclockwise sense
around the element. For example, you could use (2,4,1) instead of (1,2,4) for
the connectivity of the first element.
3. To fix motion of a node, you need to enter the node
number, the degree of freedom that is being constrained, (1 for horizontal, 2 for vertical), and a
value for the prescribed displacement.
4. To specify tractions acting on an element face, you
need to enter (a) the element number; (b) the face number of the element, and
(c,d) the horizontal and vertical components of traction acting on the
face. The face numbering scheme is determined
by the element connectivity, as follows.
Face (1) has the first and second nodes as end points; face (2) has the
second and third nodes; and face (3) has the third and first nodes as end
points. Since connectivity for element
(2) was entered as (2,3,4), face 1 of this element has nodes numbered 2 and 3;
face 2 connects nodes numbered 3 and 4, while face 3 connects nodes numbered 4
and 1.
 and enter a
name for the output file.
and enter a
name for the output file.
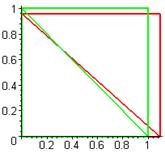
1. Return to the top of the file, and press <enter>
to execute each MAPLE block. If all goes well, you should see that, after
reading the input data, MAPLE plots the mesh (just as a check).
2. If you continue to the end, you should see a plot of
the displaced mesh (red) superimposed on the original mesh (green), as shown on
the right.
3. Finally, open the output file. It should contain the results shown below

![]() The solid is an isotropic, linear elastic
solid with Young’s modulus E and
Poisson’s ratio ;
The solid is an isotropic, linear elastic
solid with Young’s modulus E and
Poisson’s ratio ;![]() Plane
strain or plane stress deformation;
Plane
strain or plane stress deformation;![]() The solid is at constant temperature (no
thermal strains);
The solid is at constant temperature (no
thermal strains);![]() We will
neglect body forces.
We will
neglect body forces. 10.1 The finite element mesh
and element connectivity
10.1 The finite element mesh
and element connectivity
![]() They vary
linearly with position within the element
They vary
linearly with position within the element![]() Each shape
function has a value of one at one of the nodes, and is zero at the other two.
Each shape
function has a value of one at one of the nodes, and is zero at the other two. The total strain energy of the solid may be computed
by adding together the strain energy
of each element:
The total strain energy of the solid may be computed
by adding together the strain energy
of each element:![]() which contains all the
nodal displacements, rather than using for each element to describe the
displacements. For example, the strain
energy for the simple 2 element mesh shown is
which contains all the
nodal displacements, rather than using for each element to describe the
displacements. For example, the strain
energy for the simple 2 element mesh shown is We have now found a way to compute the strain energy
for a finite element
mesh. Next, we need to compute the
boundary term in the potential energy.
We have now found a way to compute the strain energy
for a finite element
mesh. Next, we need to compute the
boundary term in the potential energy. Recall that the displacements vary
linearly within a 3 noded triangle.
Therefore, we can write
Recall that the displacements vary
linearly within a 3 noded triangle.
Therefore, we can write![]() is the global residual
force vector.
is the global residual
force vector.
 The code reads an input file. A very simple input file (with just two
elements) can be found in FEM_conststrain_input.txt. A second data file
The code reads an input file. A very simple input file (with just two
elements) can be found in FEM_conststrain_input.txt. A second data file  and enter a
name for the output file.
and enter a
name for the output file.

