Chapter 14

 

Modeling Failure

 

 

One of the most important applications of solid mechanics is to design structures, components or materials that are capable of withstanding cyclic or static service loads.  To do this, you need to be able to predict the conditions necessary to cause failure.  Materials and structures can fail in many different ways, including by buckling, excessive plastic flow, fatigue and fracture, wear, or corrosion.  Calculating the stresses in a structure or component can help to design against these failures, but is usually not enough $–$ it is also necessary to understand and to be able to predict the effects of stress.

 

In this section we will discuss

1. Failure by elastic buckling
2. A brief review of the mechanisms of failure and fatigue;
3. An overview of phenomenological stress or strain based failure criteria, primarily used in design applications;
4. A brief discussion of the mechanics of cracks in solids.

 

 

14.1 Failure by geometric instability in elastic solids $–$ buckling

 

Components and structures that are subjected to compressive loading can fail by buckling.   Buckling is a form of instability that involves a form of feedback: the loads applied to a solid cause it to deform; if you are unlucky, the solid deforms in a way that causes the internal stresses to increase, leading to further deformation, and this process may continue without limit and cause complete collapse.

 

 

Simple illustration of the physics of buckling instability

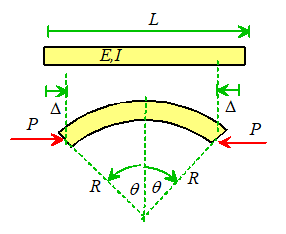
The general nature of buckling instability can be illustrated with a very simple example.   The figure shows a column subjected to axial loads.   We could try to estimate its deformed shape using the Rayleigh-Ritz method: guess the shape, and then minimize the potential energy.    Following the standard recipe:

 

1.      We guess that the beam bends into a circle with radius R (it is actually preferable to do the calculation by solving for the curvature $\kappa =1/R$ )

2.      The potential energy is

$\Pi =\frac{1}{2}EI{\kappa }^2-2P\Delta$

where $\Delta$ is the deflection of the end

3.      Simple geometry shows that

$\Delta =\frac{L}{2}-R\sin \theta =\frac{L}{2}-\frac{1}{\kappa }\sin (\kappa L/2)$

4.      We can combine 2 and 3 to get the following expression for a dimensionless potential energy

$\frac{\Pi L^2}{EI}=\frac{1}{2}{(\kappa L)}^2-\frac{P{L}^2}{EI}\left(1-\frac{2}{\kappa L}\sin (\kappa L/2)\right)$

5.      Now we can minimize the potential energy with respect to $\kappa$.   We can do this graphically: the plot below shows the variation of normalized potential energy with $\kappa L$ for several different values of $P{L}^2/EI$ 

 

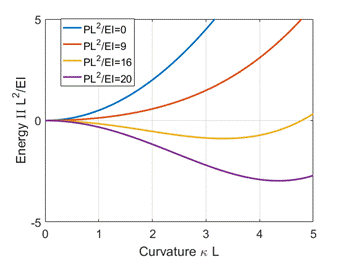
The important conclusion from this plot is that if $P{L}^2/EI$ is below about 10, then the energy is minimized with zero curvature (the beam is straight); but if $P{L}^2/EI$ exceeds 10, the energy is minimized with nonzero curvature.   The decrease in potential energy of the applied loads is greater than the increase in strain energy of the beam.    Note that the straight beam is still an equilibrium configuration $–$ but (because the energy is a maximum not a minimum) equilibrium is unstable, and a small perturbation will cause it to buckle into a curved shape.

 

It’s not hard to calculate the curvature that minimizes the energy: the result is plotted below

 

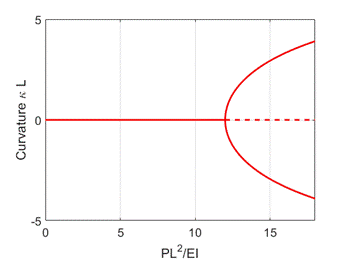
The plot shows a ‘pitchfork bifurcation’ at $P{L}^2/EI=11$ .   This is a Rayleigh-Ritz estimate, of course, which will over-estimate the buckling load.   The exact calculation shows that buckling occurs at $P{L}^2/EI={\pi }^2$, but the Rayleigh-Ritz solution is pretty good.

 

 

 

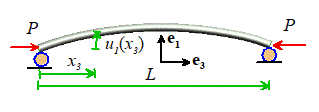Calculating Buckling Loads

 

We can show how to calculate buckling loads using a simple example.  The figure shows a straight column with Youngs modulus E, area moment of inertia $I_{22}=I,I_{12}=0$ and length L subjected to axial forces P.    Our goal is to calculate the critical value of P that will cause buckling.

 

We already know the equations governing small transverse deflections of a beam under significant axial force:

$E\left(I_{22}\frac{d^4{u}_1}{d{x}_3^4}+I_{12}\frac{d^4{u}_2}{d{x}_3^4}\right)+\rho A\frac{d^2{u}_1}{d{t}^2}=\frac{d^2{u}_1}{d{x}_3^2}{T}_3+p_1\frac{d{T}_3}{d{x}_3}+p_3\approx \rho A\frac{d^2{u}_3}{d{t}^2}$

The axial force in the rod is constant and equal to P, and we are looking for static equilibrium solutions with non-zero $u_1$ .   The equilibrium equation therefore simplifies to

$EI\frac{d^4{u}_1}{d{x}_3^4}-P\frac{d^2{u}_1}{d{x}_3^2}=0$

This equation has general solution

$A\sin k{x}_3+B\cos k{x}_3+C{x}_3+D$

The solution must satisfy the governing equation, which shows that

$\left(EI{k}^4-P{k}^2\right)\left(A\sin k{x}_3+B\cos k{x}_3\right)=0$

Nonzero solutions require that $k^2=P/EI$ .

 

Finally, the solution must satisfy zero deflection and zero bending moment at $x_3=0$ and $x_3=L$ .  This means that

$\begin{array}{l}u(0)=0\Rightarrow D=0\\ u(L)=0\Rightarrow B\cos (kL)+CL=0\\ {\frac{d^{2}u}{d{x}_3^2}|}_{x_3=0}=0\Rightarrow -B{k}^2=0\\ {\frac{d^{2}u}{d{x}_3^2}|}_{x_3=L}=0\Rightarrow -A{k}^{2}sin(kL)-B{k}^2\cos (kL)=0\end{array}$

This shows that B=C=D=0.   For nonzero A we must choose $\sin (kL)=0$  - this gives us the so-called family of ‘buckling modes’, with

$k=\frac{n\pi }{L}$

 

Each mode has a corresponding value of axial force that will just hold it in place.   The one with the lowest forces is n=1, which gives the famous Euler buckling load

$\frac{{\pi }^{2}EI}{L^2}=P$

 

To summarize the general procedure:

(1)   Find the equilibrium equation for your structure with a small deflection, and significant axial force;

(2)   The equilibrium equations will have nonzero solutions satisfying the boundary conditions for special values of the axial force; these will give the buckling load.

 

 

 

 

Calculating Buckling Loads with ABAQUS

 

1.      Set up geometry, properties, section, etc in usual way.

2.      Create part instance in assembly in usual way

3.      Create a new step after optional static step, then in the Step menu, select a ‘Linear Perturbation’ procedure, and select ‘Buckle’.  You can select the number of buckling modes you would like to extract.

4.      Apply boundary conditions in usual way.  Be sure to include a load that will cause buckling.    The load can have an arbitrary magnitude $–$ ABAQUS will compute how much the load needs to be multiplied by to cause buckling.

5.      Mesh the solid $–$ be careful with element choice (usually best to avoid reduced integration/incompatible modes as they have artificial deformation modes; also if elements will lock that will cause serious problems).  If you want to extract a large number of buckling modes you will need a fine mesh.

6.      Run job in usual way

7.      Buckling mode shapes can be displayed in Visualization Module. The ‘Eigenvalue’ reported in the viewport is the scale factor applied to the loads to just reach the buckling condition.

 

 

 

 

14.2 Summary of mechanisms of fracture and fatigue under static and cyclic loading

 

Before discussing the various approaches to modeling fracture, fatigue and failure, it is helpful to review briefly the features and mechanisms of failure in solids.

 

 

 

Failure under monotonic loading

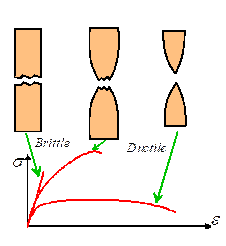
If you test a sample of any material under uniaxial tension it will eventually fail.  The features of the failure depend on several factors, including

  The materials involved and their microsctructure;

  The applied stress state (particularly the hydrostatic stress)

  Loading rate

  Temperature

  Ambient environment (water vapor; or presence of corrosive environments).

 

Materials are normally classified loosely as either `brittle’  or `ductile’ depending on the characteristic features of the failure.

 

Examples of `brittle’ materials include refractory oxides (ceramics) and intermetallics, as well as BCC metals at low temperature (below about $\mathrm{¼}$ of the melting point).  Features of a brittle material are

1. Very little plastic flow occurs in the specimen prior to failure;
2. The two sides of the fracture surface fit together very well after failure. 
3. The fracture surface appears faceted $–$ you can make out individual grains and atomic planes.
4.  In many materials, fracture occurs along certain crystallographic planes.  In other materials, fracture occurs along grain boundaries

 

Examples of `ductile’ materials include FCC metals at all temperatures; BCC metals at high temperatures; polymers at high temperature.  Features of a `ductile’ fracture are

1. Extensive plastic flow occurs in the material prior to fracture
2. There is usually evidence of considerable necking in the specimen
3. Fracture surfaces don’t fit together.
4. The fracture surface has a dimpled appearance $–$ you can see little holes, often with second phase particles inside them.

 

Of course, some materials (especially composites) have such a complex microstructure that it’s hard to classify them as entirely brittle or entirely ductile.

 

Brittle fracture often occurs as a result of a single crack propagating through the specimen.  Some materials contain pre-existing cracks, in which case fracture is initiated when one of these cracks in a region of high tensile stress starts to grow.  In other materials, the origin of the fracture is less clear $–$ various mechanisms for nucleating crack have been suggested, including dislocation pile-up at grain boundaries; or intersections of dislocations.

 

Ductile fracture occurs as a result of the nucleation, growth and coalescence of voids in the material.  Failure is controlled by the rate of nucleation of the voids; their rate of growth, and the mechanism of coalescence.  High tensile hydrostatic stress promotes rapid void nucleation and growth, but void growth generally also requires significant bulk plastic strain.

 

A ductile material may also fail as a result of plastic instability $–$ such as necking, or the formation of a shear band.  This is analogous to buckling $–$ at a critical strain, the component no longer deforms uniformly, and the deformation localizes to a small region of the solid.  This is normally accompanied by a loss of load bearing capacity and a large increase in plastic strain rate in the localized region, which eventually causes failure.

 

Finally, some materials, especially brittle materials such as glasses, and oxide based ceramics, suffer from a form of time-delayed failure under steady loading, known as `static fatigue’.  Automatic coffee-maker jugs are particularly susceptible to static fatigue.  You use one for a couple of years, and then one day it shatters if you tap it against the side of the sink.  This is because the jug’s strength has degraded with time.  Static fatigue in brittle materials is a consequence of corrosion crack growth.  The highly stressed material near a crack tip is particularly susceptible to chemical attack (the stress increases the rate of chemical reaction).  Material near the crack tip may be dissolved altogether, or it may form a reaction product with very low strength.  In either event, the crack slowly propagates through the solid, until it becomes long enough to trigger brittle fracture. Glasses and oxide based ceramics are particularly susceptible to attack by water-vapor (and perhaps coffee).

 

 

Failure under cyclic loading

 

Mechanical engineers generally have to design components to withstand cyclic as opposed to static loading.  Under cyclic loading, materials fail by fatigue.  Fatigue failure is a familiar phenomenon, but a detailed understanding of the mechanisms involved and the ability to model them quantitatively have only emerged in the past 50 years, driven largely by the demands of the aerospace industry.  There are some forms of fatigue failure (contact fatigue is an example) where the mechanisms involved are still a mystery.

 

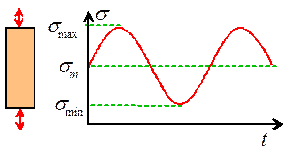Fatigue life is measured by subjecting the material to cyclic loading. The loading is usually uniaxial tension, but other cycles such as torsion or bending can be used as well. The cycle can be stress controlled (subjecting the material to a prescribed stress), or strain controlled. A cyclic uniaxial stress is usually characterized by

    The stress amplitude $({\sigma }_{\max }-{\sigma }_{\min })/2$

    The mean stress ${\sigma }_m=({\sigma }_{\max }+{\sigma }_{\min })/2$

    The stress ratio $R={\sigma }_{\min }/{\sigma }_{\max }$

 

A rotating bending test is a particularly convenient way to subject a material to a very large number of cycles in a short period of time.  The shaft can easily be spun at 2000rpm, allowing the material to be subjected to ${10}^7$ cycles in less than 100 hrs.  Pulsating tension is more common in service loading, but a servo-hydraulic tensile testing machine operating at 1Hz takes nearly 4 months to complete ${10}^7$ cycles.

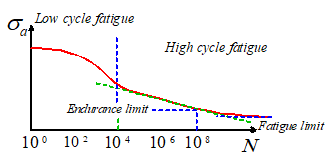
The resistance of a material to cyclic loading is characterized by plotting an `S-N’ curve showing the number of cycles to failure as a function of stress amplitude. The characteristic features of an S-N curve are illustrated in the sketch on the right.

1.      The plot normally shows two different regimes of behavior, depending on stress amplitude.

2.      At high stress levels, the material deforms plastically and fails rapidly.  In this regime the life of the specimen depends primarily on the plastic strain amplitude, rather than the stress amplitude.  This is referred to as `low cycle fatigue’ behavior.

3.      At lower stress levels life has a power law dependence on stress $–$ this is referred to as `high cycle’ fatigue behavior.

4.      In some materials, there is a clear fatigue limit $–$ if the stress amplitude lies below a certain limit, the specimen remains intact forever.  In other materials there is no clear fatigue threshold.  In this case, the stress amplitude at which the material survives ${10}^8$ cycles is taken as the endurance limit of the material. (The term `endurance’ appears to refer to the engineer doing the testing, rather than the material)

 

Fatigue life is sensitive to the mean stress, or R ratio, and tends to fall rather rapidly as R increases.  It is also influenced by environment, and temperature, and can be very sensitive to details such as the surface finish of the specimen.

 

A tensile specimen that has failed by fatigue looks at first sight as though it might have failed by brittle fracture.  The fracture surface is flat, and the two sides of the specimen fit together quite well.  In fact, for some time it was thought that some bizarre metallurgical process was responsible for turning a ductile material brittle under cyclic loading. (An engineer named Nevil Norway wrote a successful novel based on this theory.  The novel is entitled No Highway, published under the pseudonym Nevil Shute).  A closer examination reveals several differences, however.  You usually don’t see cleavage planes on a fatigue surface, and instead often observe a set of nearly parallel ridges on the surface, spaced at distances between a few 100 angstroms to a few tenths of microns apart.  These ridges are known as `striations’ and are marks left behind by the tip of a fatigue crack at each cycle of load.  In many materials, there is evidence for local areas of cleavage fracture or void coalescence interspersed with the striations.

 

Fatigue failures are caused by slow crack growth through the material.  The failure process involves four stages

1.      Crack initiation;

2.      Micro-crack growth (with crack length less than the materials grain size) (Stage I);

3.      Macro crack growth (crack length between 0.1mm and 10mm) (Stage II);

4.      Failure by fast fracture.

 

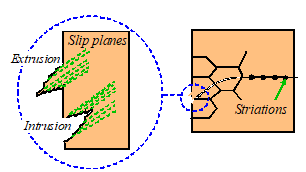
Cracks will generally only initiate in the presence of cyclic plasticity.  However, bulk plastic flow in the specimen is not necessary: plastic flow may be caused by local stress concentrations at notches in the part, due to geometric defects such as dents or scratches in the surface, or even due to microstructural features such as large inclusions in the material. In a smooth, clean specimen, the cracks form where `persistent slip bands’ reach the surface of the specimen.  Plastic flow in a material is generally highly inhomogeneous at the micron scale, with the deformation confined to narrow localized bands of slip. Where these bands intersect the surface, intrusions or extrusions form, which serve as nucleation sites for cracks. 

 

Cracks initially propagate along the slip bands at around 45 degrees to the principal stress direction $–$ this is known as Stage I fatigue crack growth.  When the cracks reach a length comparable to the materials grain size, they change direction and propagate perpendicular to the principal stress.  This is known as Stage II fatigue crack growth.

 

 

 

14.3 Stress based fracture criteria for brittle materials

 

Many of the most successful design procedures use simple, experimentally calibrated, functions of stress and strain to assess the likelihood of failure in a component.   Some examples of commonly used failure criteria are summarized in this section.

 

Stress based failure criteria for brittle solids and composites.

 

Experiments show that brittle solids (such as ceramics, glasses, and fiber-reinforced composites) tend to fail when the stress in the solid reaches a critical magnitude.   Materials such as ceramics and glasses can be idealized using an isotropic failure criterion.   Composite materials are stronger when loaded in some directions than others, and must be modeled using an anisotropic failure criterion. 

 

 Failure criteria for isotropic materials

 

The simplest brittle fracture criterion states that fracture is initiated when the greatest tensile principal stress in the solid reaches a critical magnitude,

${\sigma }_{1\max }={\sigma }_{TS}$

(The subscript TS stands for tensile strength).  To apply the criterion, you must

1.      Measure (or look up) ${\sigma }_{TS}$ for the material.  ${\sigma }_{TS}$ can be measured by conducting tensile tests on specimens $–$ it is important to test a large number of specimens because the failure stress is likely to show a great deal of statistical scatter.  The tensile strength can also be measured using beam bending tests.  The failure stress measured in a bending test is referred to as the `modulus of rupture’ ${\sigma }_r$ for the material.  It is nominally equivalent to ${\sigma }_{TS}$ but in practice usually turns out to be somewhat higher.

2.      Calculate the anticipated stress distribution in your component or structure (e.g. using FEM).  Finally, you plot contours of principal stress, and find the maximum value ${\sigma }_{1\max }$.  If  ${\sigma }_{1\max }<{\sigma }_{TS}$ the design is safe (but be sure to use an appropriate factor of safety!).

 

 

 Failure criteria for anisotropic materials

 

More sophisticated criteria must be used to model anisotropic materials (especially composites).  The criteria must take account for the fact that the material is stronger in some directions than others.  For example, a fiber reinforced composite is usually much stronger when loaded parallel to the fiber direction than when loaded transverse to the fibers.  There are many different ways to account for this anisotropy $–$ a few approaches are summarized below.

 

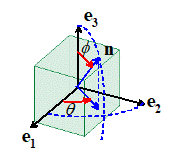Orientation dependent fracture strength.  One approach is to make the tensile strength of the solid orientation dependent.  For example, the tensile strength of a brittle, orthotropic solid (with three distinct, mutually perpendicular characteristic material directions) could be characterized by its tensile strengths ${\sigma }_{TS1},{\sigma }_{TS2},{\sigma }_{TS3}$ parallel to the three characteristic directions $\{e_1,e_2,e_3\}$ in the solid.  The tensile strength when loaded  parallel to a general direction $n=\sin \varphi \cos \theta e_1+\sin \varphi \sin \theta e_2+\cos \varphi e_3$ could be interpolated between these values as

${\sigma }_{TS}(n)=\left({\sigma }_{TS1}{\cos }^2\theta +{\sigma }_{TS2}{\sin }^2\theta \right){\sin }^2\varphi +{\sigma }_{TS3}{\cos }^2\varphi$

where $(\varphi ,\theta )$ are illustrated in the figure.  The material fails if the stress acting normal to any plane in the solid exceeds the fracture stress for that plane, i.e.

$n_i(\theta ,\varphi ){\sigma }_{ij}{n}_j(\theta ,\varphi )={\sigma }_{TS}(\varphi ,\theta )$

where ${\sigma }_{ij}$ are the stress components in the basis $\{e_1,e_2,e_3\}$.  To use this criterion to check for failure at any point in the solid, you must

(i) Find the components of stress in the  $\{e_1,e_2,e_3\}$ basis;

(ii) Maximize the function $n_i(\theta ,\varphi ){\sigma }_{ij}{n}_j(\theta ,\varphi )/{\sigma }_{TS}(\varphi ,\theta )$ with respect to $(\varphi ,\theta )$; and

(iii) Check whether the maximum value of  $n_i(\theta ,\varphi ){\sigma }_{ij}{n}_j(\theta ,\varphi )/{\sigma }_{TS}(\varphi ,\theta )$ exceeds 1.  If so, the material will fail; if not, it is safe.

 

Goldenblat-Kopnov failure criterion. A very general phenomenological failure criterion can be constructed by simply combining the stress components in a basis oriented with respect to material axes as polynomial function.  The Goldenblat-Kopnov criterion is one example, which states that the critical stresses required to cause failure satisfy the equation

$A_{ij}{\sigma }_{ij}+B_{ijkl}\sigma {}_{ij}{\sigma }_{kl}=1$

Here A and B are material constants: A is diagonal ( $A_{ij}=0i\ne j$ ) and $B$ has the same symmetries as the elasticity tensor, i.e. $B_{ijkl}=B_{klij}=B_{jikl}=B_{ijlk}$.  The most general anisotropic material would therefore be characterized by 24 independent material constants, but in practice simplified versions have far fewer parameters.  Most failure criteria for composites are in fact special cases of the Goldenblat-Kopnov criterion, including the Tsai-Hill criterion outlined below.

 

 

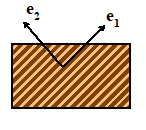Tsai-Hill criterion:  The Tsai-Hill criterion is used to model damage in brittle laminated fiber-reinforced composites and wood. A specimen of laminated composite subjected to in-plane loading is sketched in the figure.  The Tsai-Hill criterion assumes that a plane stress state exists in the solid.  Let ${\sigma }_{11},{\sigma }_{22},{\sigma }_{12}$ denote the nonzero components of stress, with basis vectors $e_1$ and $e_2$ oriented parallel and perpendicular to the fibers in the sheet, as shown.  The Tsai-Hill failure criterion is

${\left(\frac{{\sigma }_{11}}{{\sigma }_{TS1}}\right)}^2+{\left(\frac{{\sigma }_{22}}{{\sigma }_{TS2}}\right)}^2-\frac{{\sigma }_{11}{\sigma }_{22}}{{\sigma }_{TS1}^2}+\frac{{\sigma }_{12}^2}{{\sigma }_{SS}^2}=1$

at failure, where ${\sigma }_{TS1}$, ${\sigma }_{TS2}$ and ${\sigma }_{SS}$ are material properties.  They are measured as follows:

1.      The laminate is loaded in uniaxial tension parallel to the fibers. The material fails when ${\sigma }_{11}={\sigma }_{TS1}$

2.      The laminate is loaded in uniaxial tension perpendicular to the fibers.  The material fails when  ${\sigma }_{22}={\sigma }_{TS2}$

3.      In principle, the laminate could be loaded in shear $–$ it would then fail when ${\sigma }_{12}={\sigma }_{SS}$. In practice it is preferable to pull on the laminate in uniaxial tension with stress ${\sigma }_0$ at 45 degrees to the fibers, which induces stress components ${\sigma }_{11}={\sigma }_{22}={\sigma }_{12}={\sigma }_0/2$.  A simple calculation then shows that ${\sigma }_{SS}={\sigma }_{TS2}{\sigma }_0/\sqrt{4{\sigma }_{TS2}^2-{\sigma }_0^2}$.

 

 

 

Probabilistic Design Methods for Brittle Fracture  (Weibull Statistics)

 

The fracture criterion ${\sigma }_{1\max }={\sigma }_{TS}$ is too crude for many applications.  The tensile strength of a brittle solid usually shows considerable statistical scatter, because the likelihood of failure is determined by the probability of finding a large flaw in a highly stressed region of the material.  This makes it difficult to determine an unambiguous value for tensile strength $–$ should you use the median value of your experimental data?  Pick the stress level where 95% of specimens survive? It’s better to deal with this problem using a more rigorous statistical approach.

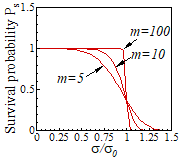
Weibull statistics refers to a technique used to predict the probability of failure in a brittle material.  The following approach is used

1.      Test a large number of samples with identical size and shape under uniform tensile stress, and determine their survival probability as a function of stress (survival probability is approximated by the fraction of specimens that survive a given stress level).

2.      Fit the survival probability of these specimens $P_s$ is fit by a Weibull distribution

$P_s(V_0)=\exp \left\{-{\left(\frac{\sigma }{{\sigma }_0}\right)}^m\right\}$

where ${\sigma }_0$ and m are material constants.  The index m is typically of the order 5-10 for ceramics, and is independent of specimen volume.  The parameter ${\sigma }_0$ is the stress at which the probability of survival is exp(-1), (about 37%). This critical stress ${\sigma }_0$ depends on the specimen volume $V_0$, and is smaller for larger specimens.

3.      Given m, ${\sigma }_0$ and the corresponding specimen volume $V_0$, the survival probability of a volume $V$ of material subjected to uniform uniaxial stress $\sigma$ follows as

$P_s(V)=\exp \left\{-\frac{V}{V_0}{\left(\frac{\sigma }{{\sigma }_0}\right)}^m\right\}$

To see this, note that the volume V can be thought of as containing $n=V/V_0$ specimens.  The probability that they all survive is ${\left\{P_s(V_0)\right\}}^n={\left\{P_s(V_0)\right\}}^{V/V_0}$.

4.      More generally, the survival probability of a solid subjected to an arbitrary stress distribution with principal values ${\sigma }_1,{\sigma }_2,{\sigma }_3$ can be computed as

$\log P_s=-\frac{1}{V_0{\sigma }_0^m}{\displaystyle \underset{V}{\int }\left({\langle {\sigma }_1\rangle }^m+{\langle {\sigma }_2\rangle }^m+{\langle {\sigma }_3\rangle }^m\right)}dV$

where

$\langle \sigma \rangle =\{\begin{array}{c}\sigma \sigma \ge 0\\ 0\sigma \le 0\end{array}$

 

This approach is quite successful in some applications: for example, it explains why brittle materials appear to be stronger in bending than in uniaxial tension.  Like many statistical approaches it has some limitations as a design tool.  The method can predict accurately the stress that gives 30% probability of failure.  But who wants to buy a product that has a 30% probability of failure?  For design applications we need to predict the probability of 1 failure in a million or so.  It is very difficult to measure the tail of a statistical distribution accurately, and a distribution that was fit to predict 63% failure probability may be wildly inaccurate in the region of interest.

 

 

14.4 Strain Based Ductile Failure Criteria

 

Strain to failure approach: Ductile fracture in tension occurs by the nucleation, growth and coalescence of voids in the material.  A crude criterion for ductile failure could be based on the accumulated plastic strain, for example

${\displaystyle \underset{}{\int }\sqrt{\frac{2}{3}d{\epsilon }_{ij}^{p}d{\epsilon }_{ij}^p}}={\epsilon }_f$

at failure, where ${\epsilon }_f$ is the plastic strain to failure in a uniaxial tensile test.

 

Porous metal plasticity: Experiments show that the strain to cause ductile failure in a material depends on the hydrostatic component of tensile stress acting on the specimen, as shown in the figure.  For example, the strain to failure under torsional loading (which subjects the material to shear with no hydrostatic stress) is much greater than under uniaxial tension. The critical strain is influenced by hydrostatic stress because ductile failure occurs as a result of the nucleation and growth of cavities in the solid.  A hydrostatic stress greatly increases the rate of growth of the cavities. The simple strain-to-failure approach cannot account for this behavior.

 

Porous metal plasticity was developed to address this issue.  The basic idea is simple: the solid is idealized as a plastic matrix which contains a volume fraction $V_f$ of cavities.  To model the solid, the plastic stress-strain laws outlined in Sections 3.6 and 3.7 are extended to calculate the volume fraction of voids in the material as part of the solution, and also to account for the weakening effect of the voids.  Failure is modeled by constructing the plastic stress-strain law so that the material loses all its strength at a critical void volume fraction.

 

Both rate independent and viscoplastic versions of porous plasticity exist.  The viscoplastic models have some advantages for finite element computations, because the rate dependence can stabilize the effects of strain softening.  A simple small-strain viscoplastic constitutive law with power-law hardening and power-law rate dependence will be outlined here to illustrate the main features of these models.  The constitutive law is known as the `Gurson model.’  

 

 

The material is characterized by the following properties:

 The Young’s modulus E and Poisson ratio $\nu$;

 A characteristic stress Y, a characteristic strain ${\epsilon }_0$ and strain hardening exponent n, which govern the strain hardening behavior of the matrix material;

 A characteristic strain rate ${\dot{\epsilon }}_0$ and strain rate exponent m, which govern the strain rate sensitivity of the solid;

 A constant $N_v$, which controls the rate of void nucleation with plastic straining;

 The flow strength of the matrix ${\sigma }_0$, the void volume fraction, $V_f$, and the total accumulated effective plastic strain in the matrix material ${\overline{\epsilon }}_m$ which all evolve with plastic straining.

The constitutive equations specify a relationship between the stress ${\sigma }_{ij}$ applied to the material and the resulting strain rate ${\dot{\epsilon }}_{ij}$, as follows

1.      The strain rate is decomposed into elastic and plastic parts  as ${\dot{\epsilon }}_{ij}={\dot{\epsilon }}_{ij}^e+{\dot{\epsilon }}_{ij}^p$;

2.      The elastic part of the strain rate is related to the stress rate by the linear elastic constitutive equations

${\dot{\epsilon }}_{ij}^e=\frac{1+\nu }{E}{\dot{\sigma }}_{ij}-\frac{\nu }{E}{\dot{\sigma }}_{kk}{\delta }_{ij}$

3.      The magnitude of the plastic strain rate is determined by the following plastic flow potential

${\dot{\epsilon }}_e=g({\sigma }_e,p,{\sigma }_0,V_f)={\dot{\epsilon }}_0{\left[{\left(\frac{{\sigma }_e}{{\sigma }_0}\right)}^2+2V_f\cosh \left(\frac{3p}{2{\sigma }_0}\right)-V_f^2\right]}^{m/2}$

where ${\dot{\epsilon }}_e=2{\dot{\epsilon }}_{ij}^p{\dot{\epsilon }}_{ij}^p/3$ ${\sigma }_e=\sqrt{3S_{ij}{S}_{ij}/2}$, $p={\sigma }_{kk}/3$ and $S_{ij}={\sigma }_{ij}-p{\delta }_{ij}$.  Note that for $V_f>0$ the plastic strain rate increases with hydrostatic stress p.

4.       The components of the plastic strain rate tensor are computed from an associated flow law

$\begin{array}{l}{\dot{\epsilon }}_{ij}^p=\sqrt{\frac{3}{2}}\frac{g({\sigma }_e,p,{\sigma }_0,V_f)}{{\left[\left(\partial g/\partial {\sigma }_{kl}\right)\left(\partial g/\partial {\sigma }_{kl}\right)\right]}^{1/2}}\frac{\partial g}{\partial {\sigma }_{ij}}\\ =\frac{g({\sigma }_e,p,{\sigma }_0,V_f)}{\sqrt{{\sigma }_e^2/{\sigma }_0^2+(V_f^2/2){\sinh }^2(3p/2{\sigma }_0)}}\left\{\frac{3}{2}\frac{S_{ij}}{{\sigma }_0}+\frac{V_f}{2}\sinh \left(\frac{3p}{2{\sigma }_0}\right){\delta }_{ij}\right\}\end{array}$

5.      Strain hardening in the matrix is modeled by relating its flow stress ${\sigma }_0$ to the accumulated strain in the matrix ${\overline{\epsilon }}_m$. The following power-law hardening model is often used

${\sigma }_0=Y{\left(1+{\overline{\epsilon }}_m/{\epsilon }_0\right)}^{1/n}$

6.      The effective plastic strain in the matrix is calculated from the condition that the plastic dissipation in the matrix must equal the rate of work done by stresses, which requires that

$(1-V_f){\sigma }_0{\dot{\overline{\epsilon }}}_m={\sigma }_{ij}{\dot{\epsilon }}_{ij}^p\Rightarrow {\dot{\overline{\epsilon }}}_m=\frac{g({\sigma }_e,p,{\sigma }_0,V_f)}{(1-V_f)}\left(\frac{{\sigma }_e^2}{{\sigma }_0^2}+\frac{3p}{2{\sigma }_0}{V}_f\sinh \left(\frac{3p}{2{\sigma }_0}\right)\right)$

7.      Finally, the model is completed by specifying the void volume fraction as a function of strain.  The void volume fraction can increase due to growth of existing voids, or nucleation of new ones. To account for both effects, one can set

${\dot{V}}_f=(1-V_f){\dot{\epsilon }}_{kk}^p+N_v{\dot{\epsilon }}_e$

where the first term accounts for void growth, and the second accounts for strain controlled void nucleation. 

 

Ductile failure by strain localization

 

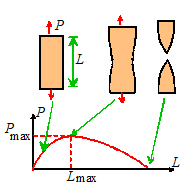If you test a cylindrical specimen of a very ductile material in uniaxial tension, it will initially deform uniformly, and remain cylindrical. At a critical load (or strain) the specimen will start to neck, as shown in the picture.  Necking, once it starts, is usually unstable $–$ there is a concentration in stress near the necked region, increasing the rate of plastic flow near the neck compared with the rest of the specimen, and so increasing the rate of neck formation.   The strains in the necked region rapidly become very large, and quickly lead to failure.

 

Neck formation is a consequence of geometric softening.  A very simple model explains the concept of geometric softening.

1.      Consider a cylindrical specimen with initial cross sectional area $A_0$ and length $L_0$. The specimen is subjected to a load P, which deforms the material plastically. After straining, the length of the specimen increases to L, and its cross-sectional area decreases to A.

2.      Assume that the material is perfectly plastic and has a true stress-strain curve (Cauchy stress $–$v- logarithmic strain) that can be approximated by a power-law $\sigma ={\sigma }_0{\epsilon }^n$ with n<1.

3.      The true strain in the specimen is related to its length by $\epsilon =\log \frac{L}{L_0}$

4.      The force on the specimen is related to the Cauchy stress by $P=A\sigma =A{\sigma }_0{\epsilon }^n$

5.      At the point of maximum load $\frac{dP}{dL}=\frac{dA}{dL}\sigma +A\frac{d\sigma }{dL}=0$

6.      We can calculate $dA/dL$ by noting that the volume of the specimen is constant during plastic straining, which shows that

$AL=A_0{L}_0\Rightarrow \frac{dA}{dL}L+A=0\Rightarrow \frac{dA}{dL}=-\frac{A}{L}$

Notice that $dA/dL$ is negative $–$ this means that the specimen tends to soften as a result of the change in its cross sectional area.  This is what is meant by geometric softening.

7.      We can calculate $d\sigma /dL$ from (2) and (3) as follows

$\frac{d\sigma }{dL}=\frac{d\sigma }{d\epsilon }\frac{d\epsilon }{dL}=\frac{n{\sigma }_0{\epsilon }^{n-1}}{L}$

Notice that $d\sigma /dL$ is positive $–$ strain hardening in the material tends to compensate for the effects of geometric softening.

8.      Finally, substituting the results of (6) and (7) back into (5) and recalling that  $\sigma ={\sigma }_0{\epsilon }^n$ shows that at the point of maximum load, the strain and length of the specimen are

$-\frac{A\sigma }{L}+A\frac{n{\sigma }_0{\epsilon }^{n-1}}{L}=0\Rightarrow {\epsilon }_{\max }=n\Rightarrow L_{\max }=L_0\exp (n)$

9.      Finally, note that by volume conservation the cross sectional area is $A=A_0{L}_0/L$, so the maximum load the specimen can withstand follows as

$P_{\max }=A{\sigma }_{\max }=\frac{A_0{L}_0}{L}{\sigma }_0{({\epsilon }_{\max })}^n=A_0{\sigma }_0{n}^n\exp (-n)$

It turns out that the point of maximum load coincides with the condition for unstable neck formation in the bar.  This is plausible $–$ a falling load displacement curve is always a sign that there might be a possibility of non-unique solutions $–$ but a rather sophisticated calculation is required to show this rigorously.

 

There are two important points to take away from this discussion.

    Plastic localization, as opposed to material failure, may limit load bearing capacity;

    If you measure the strain to failure of a material in uniaxial tension, it is possible that you have not measured the inherent strength of the material $–$ your specimen may have failed due to a geometric effect.  Material behavior does influence the strain to failure, of course: the simple analysis of geometric softening shows that the strain hardening behavior of the material is critical. 

 

Plastic localization can occur for many reasons.  There are two general classes of localization $–$ it may occur as a consequence of changes in specimen geometry (i.e. geometric softening); or it may occur due to a natural tendency of the material itself to soften at large strains.

 

Examples of geometry induced localization are

1.      Neck formation in a bar under uniaxial tension;

2.      Shear band formation in torsional or shear loading at high strain rate due to thermal softening as a result of plastic heat generation

 

Examples of material induced localization are

1.      Localization in a Gurson solid due to the softening effect of voids at large strains;

2.      Localization in a single crystal due to the softening effect of lattice rotations;

3.      Localization in a brittle microcracking material due to the increase in elastic compliance caused by the cracks.

 

Geometric localization can be modeled quite easily, because it does not rely on any empirical failure criteria.  A straightforward FEM computation, with an appropriate constitutive law and proper consideration of finite strains, will predict localization if it is going to occur $–$ the only thing you need to worry about is to be sure you understand what triggered the localization.  Localization can start at a geometric imperfection in the model, in which case your prediction is meaningful (but may be sensitive to the nature of the imperfection).  It may also be triggered by numerical errors, in which case the predicted failure load is meaningless.  It is usually exceedingly difficult to compute what happens after localization.  Fortunately it’s rather rare to need to do this for design purposes.

 

 

 

14.5 Criteria for Failure Under Cyclic Loading

 

 

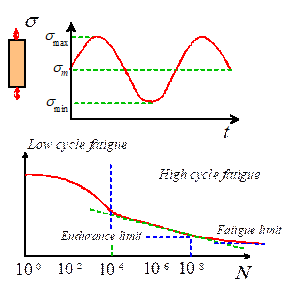High cycle fatigue under constant amplitude cyclic loading

 

Empirical stress or strain based life prediction methods are extensively used in design applications.  The approach is straightforward $–$ subject a sample of the material to a cycle of stress (or strain) that resembles service loading, in an environment representative of service conditions, and measure its life as a function of stress (or strain) amplitude, then fit the data with a curve.

 

Here we will review criteria that are used to predict fatigue life under proportional cyclic loading. A typical stress cycle is parameterized by its amplitude $({\sigma }_{\max }-{\sigma }_{\min })/2$ and the mean stress ${\sigma }_m=({\sigma }_{\max }+{\sigma }_{\min })/2$

 

For tests run in the high cycle fatigue regime with any fixed value of mean stress, the relationship between stress amplitude ${\sigma }_a$ and the number of cycles to failure N is fit well by Basquin’s Law

${\sigma }_a{N}^b=C$

where the exponent b is typically between 0.05 and 0.15.  The constant C is a function of mean stress.

 

There are two ways to account for the effects of mean stress.  Both are based on the same idea: we know that if the mean stress is equal to the tensile strength of the material $\sigma ={\sigma }_{UTS}$, it will fail in 0 cycles of loading.  We also know that for zero mean stress, the fatigue life obeys Basquin’s law.  We can interpolate between these two points.  There are two ways to do this:

 Goodman’s rule uses a linear interpolation, giving

${\sigma }_a{N}^b=C_0\left(1-\frac{{\sigma }_m}{{\sigma }_{UTS}}\right)$

where $C_0$ is the constant in Basquin’s law determined by testing at zero mean stress.

 Gerber’s rule uses a parabolic fit

${\sigma }_a{N}^b=C_0\left\{1-{\left(\frac{{\sigma }_m}{{\sigma }_{UTS}}\right)}^2\right\}$

In practice, experimental data seem to lie between these two limits.  Goodman’s rule gives a safe estimate.

 

These criteria are intended to be used for components that are subjected to uniaxial tensile stress.  The criteria can still be used if the loading is proportional (i.e. with fixed directions of principal stress).  In this case, the maximum principal stress should be used to calculate ${\sigma }_a$ and ${\sigma }_m$.  They do not work under non-proportional loading.   A very large number of fatigue models have been developed for more general loading conditions $–$ a review can be found in Liu and Mahadevan, Int J. Fatigue, 27 790-800 (2005).

 

 

Criteria for failure by low cycle fatigue

 

If a fatigue test is run with a high stress level (sufficient to cause plastic flow in a large section of the solid) the specimen fails very quickly (less than 10 000 cycles).  This regime of behavior is known as `low cycle fatigue’.  The fatigue life correlates best with the plastic strain amplitude rather than stress amplitude, and it is found that the Coffin Manson Law

$\Delta {\epsilon }^p{N}^b=C$

gives a good fit to empirical data (the constants C and b do not have the same values as for Basquin’s law, of course)