Chapter 4
Mathematical description of shape
changes in solids
 In this section, we list the various mathematical
formulas that are used to characterize shape changes in solids (and in
fluids). The formulas might look scary
at first, but they are mostly just definitions.
In this section, we list the various mathematical
formulas that are used to characterize shape changes in solids (and in
fluids). The formulas might look scary
at first, but they are mostly just definitions.
As
you work through the various definitions, you should bear in mind that shape changes near a point can always be
characterized by six numbers. These
could be could be the six independent components of the Lagrangian strain, Eulerian
strain, the left or right stretch tensors, or your own favorite deformation
measure. Given the complete set of six
numbers for any one deformation measure, you can always calculate the
components of other strain measures. The reason that so many different
deformation measures exist is partly that different material models adopt
different strain measures, and partly because each measure is useful for
describing a particular type of shape change.
4.1 The Displacement and Velocity
Fields
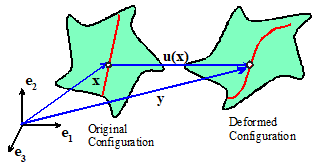
The displacement vector u(x,t) describes the motion of each point in the solid. To make this
precise, visualize a solid deforming under external loads. Every point in the solid moves as the load is
applied: for example, a point at position x
in the undeformed solid might move to a new position y at time t. The displacement vector is defined as
We could also express this formula using index notation, as
Here, the subscript i has values 1,2, or 3, and (for example) represents the three Cartesian components of
the vector y.
The displacement field completely specifies the change
in shape of the solid. The velocity field
would describe its motion, as
Examples
of some simple deformations
|
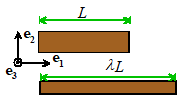
 Volume
preserving uniaxial extension Volume
preserving uniaxial extension
|
|
|
|
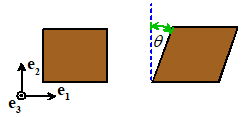
 Simple shear Simple shear
|
|
|
|
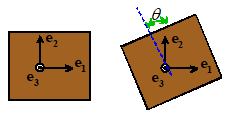
 Rigid rotation through angle about axis Rigid rotation through angle about axis
|
|
|
 General rigid rotation about the origin General rigid rotation about the origin
where R must satisfy ,
det(R)>0. (i.e. R is proper orthogonal). I is the identity tensor with components
Alternatively, a rigid rotation through angle (with right hand screw convention) about an
axis through the origin that is parallel to a unit vector n can be written as
The components of R are
thus
where is the permutation
symbol, satisfying
|
|
|
 General homogeneous deformation General homogeneous deformation
or
where are
constants.
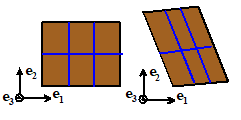
The physical significance of a homogeneous
deformation is that all straight lines in the solid remain straight under the
deformation. Thus, every point in the
solid experiences the same shape change.
All the deformations listed above are examples of homogeneous
deformations.
|
|
4.2 The Displacement gradient and
Deformation gradient tensors
These
quantities are defined by
 Displacement
Gradient Tensor: is a tensor with components
Displacement
Gradient Tensor: is a tensor with components
Deformation
Gradient Tensor:
where I is
the identity tensor, with components described by the Kronekor delta symbol:
and represents the gradient operator. Formally,
the gradient of a vector field u(x) is defined so that
but
in practice the component formula is more useful.
Note also that
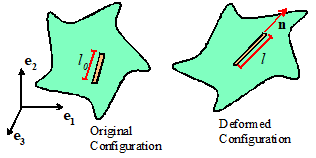
 The concepts of displacement gradient and deformation
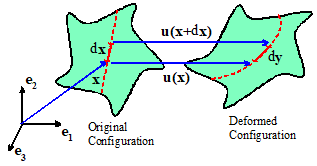
gradient are introduced to quantify the change in shape of infinitesimal line
elements in a solid body. To see this, imagine drawing a straight line on the undeformed
configuration of a solid, as shown in the figure. The line would be mapped to a smooth curve on
the deformed configuration. However,
suppose we focus attention on a line segment dx, much shorter than the radius of curvature of this curve, as
shown. The segment would be straight in
the undeformed configuration, and would also be (almost) straight in the
deformed configuration. Thus, no matter
how complex a deformation we impose on a solid, infinitesimal line segments are
merely stretched and rotated by a deformation.The infinitesimal line segments dx and dy are related by
The concepts of displacement gradient and deformation
gradient are introduced to quantify the change in shape of infinitesimal line
elements in a solid body. To see this, imagine drawing a straight line on the undeformed
configuration of a solid, as shown in the figure. The line would be mapped to a smooth curve on
the deformed configuration. However,
suppose we focus attention on a line segment dx, much shorter than the radius of curvature of this curve, as
shown. The segment would be straight in
the undeformed configuration, and would also be (almost) straight in the
deformed configuration. Thus, no matter
how complex a deformation we impose on a solid, infinitesimal line segments are
merely stretched and rotated by a deformation.The infinitesimal line segments dx and dy are related by
Written
out as a matrix equation, we have
To derive this result, consider an infinitesimal line
element dx in a deforming
solid. When the solid is deformed, this
line element is stretched and rotated to a deformed line element dy. If
we know the displacement field in the solid, we can compute dy=[x+dx+u(x+dx)]-[x+u(x)] from the
position vectors of its two end points
Expand
as a Taylor
series
so
that
We
identify the term in parentheses as the deformation gradient, so
The inverse
of the deformation gradient arises in many calculations. It is defined through
or
alternatively
4.3 Deformation gradient resulting
from two successive deformations
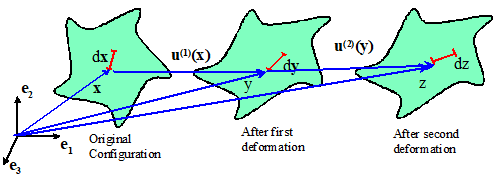
Suppose that
two successive deformations are applied to a solid, as shown. Let
map infinitesimal line elements from the original
configuration to the first deformed shape, and from the first deformed shape to
the second, respectively, with
The
deformation gradient that maps infinitesimal line elements from the original
configuration directly to the second deformed shape then follows as
Thus, the
cumulative deformation gradient due to two successive deformations follows by
multiplying their individual deformation gradients.
To see this,
write the cumulative mapping as and apply the chain rule
4.4 The Jacobian of the deformation
gradient
The
Jacobian is defined as
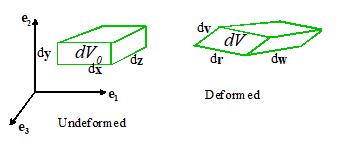
It is a measure of the volume change produced by a
deformation. To see this, consider the
infinitessimal volume element shown with sides dx, dy, and dz in the figure above. The original
volume of the element is
Here,
 is the permutation
symbol. The element is mapped to a paralellepiped with sides dr,
dv, and dw
with volume given by
is the permutation
symbol. The element is mapped to a paralellepiped with sides dr,
dv, and dw
with volume given by
Recall
that
so
that
Recall
that
so
that
Hence
Observe
that
 For any physically admissible deformation, the
volume of the deformed element must be positive (no matter how much you deform
a solid, you can’t make material disappear).
Therefore, all physically admissible displacement fields must satisfy J>0
For any physically admissible deformation, the
volume of the deformed element must be positive (no matter how much you deform
a solid, you can’t make material disappear).
Therefore, all physically admissible displacement fields must satisfy J>0
 If a material is incompressible, its volume remains constant. This requires J=1.
If a material is incompressible, its volume remains constant. This requires J=1.
 If the mass
density of the material at a point in the undeformed solid is , its mass density in the deformed solid
is
If the mass
density of the material at a point in the undeformed solid is , its mass density in the deformed solid
is
Derivatives
of J. When working with constitutive
equations, it is occasionally necessary to evaluate derivatives of J with respect to the components of F.
The following result (which can be proved e.g. by expanding the Jacobian
using index notation) is extremely useful
4.5 The
Lagrange strain tensor
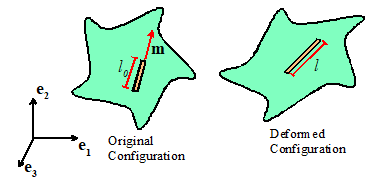 The Lagrange strain tensor is defined as
The Lagrange strain tensor is defined as
The components of Lagrange strain can also be
expressed in terms of the displacement gradient as
The Lagrange strain tensor quantifies the changes in
length of a material fiber, and angles between pairs of fibers in a deformable
solid. It is used in calculations where
large shape changes are expected.
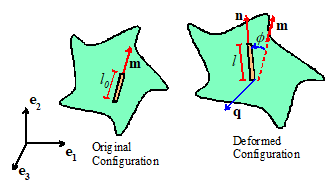
To visualize the physical significance of E, suppose we mark out an imaginary
tensile specimen with (very short) length 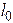 on our deforming
solid, as shown in the picture. The orientation of the specimen is arbitrary,
and is specified by a unit vector m,
with components . Upon deformation, the specimen increases in
length to .
Define the strain of the specimen as
on our deforming
solid, as shown in the picture. The orientation of the specimen is arbitrary,
and is specified by a unit vector m,
with components . Upon deformation, the specimen increases in
length to .
Define the strain of the specimen as
Note that this definition of strain is similar to the
definition you are familiar with, but contains an
additional term. The additional term is
negligible for small .
Given the Lagrange strain components ,
the strain of the specimen may be computed from
We
proceed to derive this result. Note that
is an infinitesimal vector with length and orientation
of our undeformed specimen. From the
preceding section, this vector is stretched and rotated to
The length of the deformed specimen is equal to the
length of dy, so we see that
Hence, the strain for our line element is
giving
the results stated.
Example 1: Calculate the deformation gradient and Lagrange strain
tensor for a volume preserving uniaxial deformation described by the mapping

Check
that the mapping does preserve volume.
This
is just a matter of substituting into the formulas
Hence
You
can see that det(F)=1, so the
mapping is volume preserving
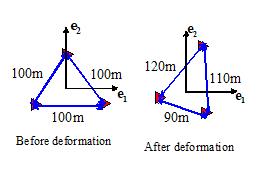 Example 2: To track the
deformation in a slowly moving glacier, three survey stations are installed in
the shape of an equilateral triangle, spaced 100m apart, as shown in the
picture. After a suitable period of
time, the spacing between the three stations is measured again, and found to be
90m, 110m and 120m, as shown in the figure.
Assuming that the deformation of the glacier is homogeneous over the
region spanned by the survey stations, please compute the components of the
Lagrange strain tensor associated with this deformation, expressing your answer
as components in the basis shown.
Example 2: To track the
deformation in a slowly moving glacier, three survey stations are installed in
the shape of an equilateral triangle, spaced 100m apart, as shown in the
picture. After a suitable period of
time, the spacing between the three stations is measured again, and found to be
90m, 110m and 120m, as shown in the figure.
Assuming that the deformation of the glacier is homogeneous over the
region spanned by the survey stations, please compute the components of the
Lagrange strain tensor associated with this deformation, expressing your answer
as components in the basis shown.
Recall that the initial and
deformed lengths of a material element parallel to a unit
vector in the undeformed configuration are related by
The three unit vectors
parallel to the sides of the triangle are . Multiplying out the vectors for the three
sides of the triangle gives
These three equations can be
solved for the Lagrange strain components, with the result
or
4.6 The
Infinitesimal strain tensor
The
infinitesimal strain tensor is defined as
where
u is the displacement vector. Written out in full
The infinitesimal
strain tensor is an approximate
deformation measure, which is only valid for small shape changes. It
is more convenient than the Lagrange or Eulerian strain, because it is linear.
Specifically, suppose the deformation gradients are
small, so that all .
Then the Lagrange strain tensor is
so the infinitesimal strain approximates the Lagrange
strain. You can show that it also
approximates the Eulerian strain with the same accuracy.
Properties of the infinitesimal strain
tensor
 For small strains, the engineering strain of
an infinitesimal fiber aligned with a unit vector m can be estimated as
For small strains, the engineering strain of
an infinitesimal fiber aligned with a unit vector m can be estimated as
 Note that
Note that
 (see below for
more details)
(see below for
more details)
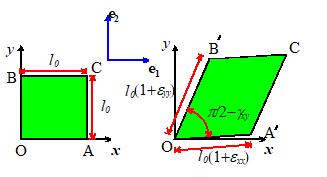
 The infinitesimal strain tensor is closely
related to the strain matrix introduced in elementary strength of materials
courses. For example, the physical
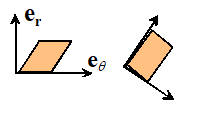
significance of the (2 dimensional) strain matrix
The infinitesimal strain tensor is closely
related to the strain matrix introduced in elementary strength of materials
courses. For example, the physical
significance of the (2 dimensional) strain matrix
is illustrated in the
figure.
To relate this to the infintesimal strain tensor, let be a Cartesian basis, with parallel to x and parallel to y as shown. Let denote the components of the infinitesimal
strain tensor in this basis. Then
4.7 Engineering shear strains
For a general strain tensor (which could be any of ,
or ,
among others), the diagonal strain components are known as `direct’ strains, while the off
diagonal terms are known as ‘shear strains’
The shear strains are sometimes reported as ‘Engineering
Shear Strains’ which are related to the formal definition by a factor of 2 i.e.
This factor of 2 is an endless source of
confusion. Whenever someone reports
shear strain to you, be sure to check which definition they are using. In particular, many commercial finite element
codes output engineering shear strains.
4.8
Decomposition of infinitesimal strain into volumetric and deviatoric parts
The
volumetric infinitesimal strain is
defined as
The
deviatoric infinitesimal strain is
defined as
The
volumetric strain is a measure of volume changes, and for small strains is
related to the Jacobian of the deformation gradient by . To see this, recall that
The
deviatioric strain is a measure of shear deformation (shear deformation
involves no volume change).
4.9 The
Infinitesimal rotation tensor
The
infinitesimal rotation tensor is defined as
Written
out as a matrix, the components of  are
are
Observe
that is skew
symmetric: .
A skew tensor represents a rotation through a small
angle. Specifically, the operation ..
rotates the infinitesimal line element through a small angle about an axis parallel to the unit vector . (A skew tensor also sometimes represents an
angular velocity).
To visualize the significance of ,
consider the behavior of an imaginary, infinitesimal, tensile specimen embedded
in a deforming solid. The specimen is
stretched, and then rotated through an angle about some axis q. If the displacement
gradients are small, then .
The rotation of the specimen depends on its original
orientation, represented by the unit vector m. One can show (although one
would rather not do all the algebra) that represents the average rotation, over all possible orientations of m, of material fibers passing through a
point.
As
a final remark, we note that a general deformation can always be decomposed
into an infinitesimal strain and rotation
Physically,
this sum of and can be regarded as representing two successive
deformations a small strain, followed by a rotation, in the
sense that
first
stretches the infinitesimal line element, then rotates it.
4.10
Principal values and directions of the infinitesimal strain tensor
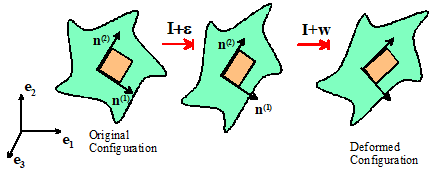
The three principal values and directions of the infinitesimal strain tensor satisfy
Clearly, and are the eigenvalues and eigenvectors of . There are three principal strains and three
principal directions, which are always mutually perpendicular.
Their significance can be visualized as follows.
1. Note that the decomposition can be visualized as a small strain, followed
by a small rigid rotation, as shown in the picture.
2. The formula indicates
that a vector n is mapped to
another, parallel vector by the strain.
3. Thus, if you draw a small cube with its faces
perpendicular to on the undeformed solid, this cube will be
stretched perpendicular to each face, with a fractional increase in length . The faces remain perpendicular to after deformation.
4. Finally, w
rotates the small cube through a small angle onto its configuration in the
deformed solid.
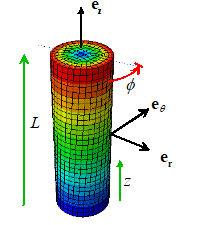
Example: The twisted cylinder shown in the figure has a
displacement field (in polar coordinates)
where
is the angle of twist at the end of the
cylinder. The contours show the
magnitude of the displacement vector, to help visualize the deformation.
(a)
Calculate the infinitesimal strain tensor in the cylinder. Hence determine the engineering shear strains
We
need the cylindrical-polar formulas for the gradient of a vector v from Section 3.6 of the notes
In
the problem here and all the other displacement components are
zero. Therefore
The
infinitesimal strain tensor follows as
The
engineering shear strains (which you may remember from intro courses) is . Note
the factor of 2.
(b)
Calculate the Lagrange strain tensor in the bar. Find a formula for the difference between
the infinitesimal strain and the Lagrange strain.
It
gets a bit tedious to do these problems by hand so here is a Matlab Live Script
solution
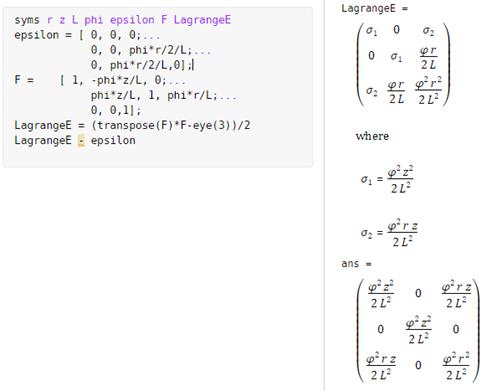
Note
that as long as the twist angle is small, the infinitesimal strain is
approximately equal to the Lagrange strain.
(c)
Calculate the principal strains and the directions of the principal strains
More
Live Scripts
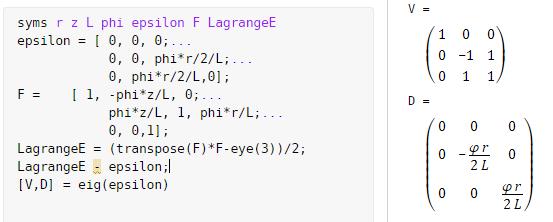
 The matrix V contains the three eigenvectors as
columns (they are not unit vectors). The
matrix D contains the principal strain values on the diagonals. The principal strain directions are therefore
at 45 degrees to the directions.
The deformation of a square element is illustrated in the figure below. The volume is constant; and the element is
stretched parallel to one principal direction, and compressed parallel to the
other.
The matrix V contains the three eigenvectors as
columns (they are not unit vectors). The
matrix D contains the principal strain values on the diagonals. The principal strain directions are therefore
at 45 degrees to the directions.
The deformation of a square element is illustrated in the figure below. The volume is constant; and the element is
stretched parallel to one principal direction, and compressed parallel to the
other.
4.11
Cauchy-Green Deformation Tensors
The Cauchy-Green deformation tensors are used to model
highly deformable solids such as rubbers or tissue. They are defined through
 The
Right Cauchy Green Deformation Tensor
The
Right Cauchy Green Deformation Tensor
 The
Left Cauchy Green Deformation Tensor
The
Left Cauchy Green Deformation Tensor
They are called `left’ and `right’ tensors because of
their relation to the `left’ and ‘right’ stretch tensors defined below. They can be regarded as quantifying the
squared length of infinitesimal fibers in the deformed configuration, by noting
that if a material fiber in the undeformed solid is stretched and
rotated to in the deformed solid, then
4.12 Rotation tensor, and Left and Right Stretch
Tensors
The
definitions of these quantities are
 The
Right Stretch Tensor
The
Right Stretch Tensor
 The
Left Stretch Tensor
The
Left Stretch Tensor
 The
Rotation Tensor
The
Rotation Tensor
To calculate these quantities you need to remember how
to calculate the square root of a matrix.
For example, to calculate the square root of C, you must
1. Calculate the eigenvalues of C we will call these ,
with n=1,2,3. Since C
and B are both symmetric and
positive definite, the eigenvalues are all positive real numbers, and therefore
their square roots are also positive real numbers.
2. Calculate the eigenvectors of C and normalize them so they
have unit magnitude. We will denote
the eigenvectors by . They must be normalized to satisfy
3. Finally, calculate ,
where denotes a dyadic product In components, this
can be written
4. As an additional bonus, you can quickly compute the
inverse square root (which is needed to find R) as
Of
course, MATLAB or similar codes will do these operations for you easily.
To
see the physical significance of these tensors, observe that
1.
The definition of
the rotation tensor shows that
2. The multiplicative decomposition of a constant tensor can be regarded as a sequence of two homogeneous
deformations U,
followed by R. Similarly, is R followed
by V.
3. R is proper orthogonal (it satisfies and det(R)=1),
and therefore represents a rotation. To
see this, note that U is symmetric,
and therefore satisfies ,
so that
and det(R)=det(F)det(U-1)=1
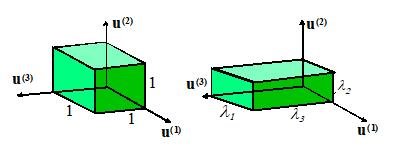
- U can be expressed in the form
where are the three (mutually perpendicular)
eigenvectors of U. (By construction,
these are identical to the eigenvectors of C). If we interpret as basis vectors, we see that U is diagonal in this basis, and so corresponds to stretching parallel
to each basis vector, as shown in the figure below.
The
decompositions
and
are known as the right
and left polar decomposition of F. (The right and left refer to the
positions of U and V).
They show that every homogeneous deformation can be decomposed into a
stretch followed by a rigid rotation, or equivalently into a rigid rotation
followed by a stretch. The decomposition is discussed in more detail in the
next section.
4.13 Principal stretches
The
principal stretches can be calculated from any one of the following (they all
give the same answer)
- The eigenvalues of the right stretch tensor U
- The eigenvalues of the left stretch tensor V
- The square root of the eigenvalues of the right
Cauchy-Green tensor C
- The square root of the eigenvalues of the left
Cauchy-Green tensor B
The
principal stretches are also related to the eigenvalues of the Lagrange and
Eulerian strains. The details are left
as an exercise.
There
are two sets of principal stretch
directions, associated with the undeformed and deformed solids.
- The principal stretch
directions in the undeformed
solid are the (normalized) eigenvectors of U or C. Denote these by .
- The principal stretch
directions in the deformed solid
are the (normalized) eigenvectors of V
or B. Denote these by .
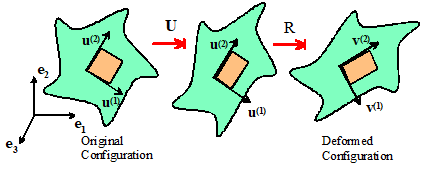 To visualize the physical significance of principal
stretches and their directions, note that a deformation can be decomposed as into a sequence of a stretch followed by a
rotation.
To visualize the physical significance of principal
stretches and their directions, note that a deformation can be decomposed as into a sequence of a stretch followed by a
rotation.
Note
also that
- The principal
directions are mutually perpendicular. You could draw a little cube on the
undeformed solid with faces perpendicular to these directions, as shown
above.
- The stretch U will stretch the cube by an
amount parallel to each . The faces of the stretched cube remain
perpendicular to .
- The rotation R will rotate the stretched cube
so that the directions rotate to line up with .
- The faces of the deformed cube are perpendicular
to
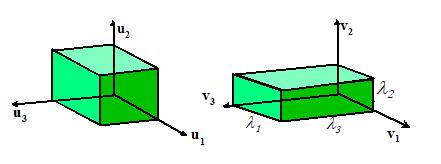
The
decomposition can be visualized in much the same way. In this case, the directions are first rotated to coincide with . The cube is then stretched parallel to each to produce the same shape change.
We could compare the undeformed and deformed cubes by
placing them side by side, with the vectors and parallel, as shown in the figure.
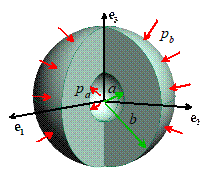 Example: a spherical shell (see the figure) is made from an
incompressible material. In its
undeformed state, the inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation
Example: a spherical shell (see the figure) is made from an
incompressible material. In its
undeformed state, the inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation
(a) Calculate the components of the deformation gradient
tensor
It is fastest to do this with index notation. Remember (see the examples at the end of
Sect 3.7)
Hence
(b) Verify that the deformation is volume preserving
Since the deformation is
radially symmetric, we can compute J
along any radial line. Taking ,
we see that
(c) Find the deformed length of an infinitesimal
radial line that has initial length ,
expressed as a function of R
Let . Then and .
(d) Find the deformed length
of an infinitesimal circumferential line that has initial length ,
expressed as a function of R
Since the deformation is volume preserving,
(e) Using the
results of (c) and (d), write down the principal stretches for the deformation.
If is
a principal stretch direction, the principal stretches have the property that (no sum on i). The principal stretch directions are radial
and circumferential, by inspection.
From (c) and (d), it follows that .
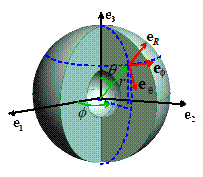 Example: Repeat problem (a) from above, but this time
solve the problem using spherical-polar coordinates, using the various formulas
for vector and tensor operations given in Section 3.5 of the notes. In this case, you may assume that a point
with position in the undeformed solid has position vector
Example: Repeat problem (a) from above, but this time
solve the problem using spherical-polar coordinates, using the various formulas
for vector and tensor operations given in Section 3.5 of the notes. In this case, you may assume that a point
with position in the undeformed solid has position vector
after deformation.
We need the following result
from Section 3.5: the gradient of a
vector with components is
For our problem
Hence
Alternatively we can do the
calculation using the gradient operator
and
the derivatives of the basis vectors are
Then the deformation
gradient is:
These
are far simpler than the Cartesian form that’s why we use spherical coordinates!
Example: The figure shows the reference and deformed
configurations for a solid. The
out-of-plane dimensions are unchanged.
Points a and b are the positions of points A and B after
deformation. Determine

(a) The right stretch tensor U, expressed as components in . (A 2x2 matrix is sufficient).
The deformed configuration
can be reached by a stretch parallel to the two basis vectors, followed by a
rotation. These can be taken to be the
two deformations in the decomposition F=RU
(b) The rotation tensor R in the polar decomposition of the deformation
gradient F=RU=VR
The bar is rotated 45
degrees in the counterclockwise direction.
Using the formula from section 4.1 we know that
(c) The deformation gradient, expressed as
components in . Try to do this without using the basis-change
formulas.
The deformation gradient
can be decomposed as F=VR, and V has components
in ,
while R has the same components in
both and . Therefore
4.14
Generalized strain measures
The polar decompositions and provide a way to define additional strain
measures. Let denote the principal stretches, and let and denote the normalized eigenvectors of U and V. Then one could define strain
tensors through
The
correspoinding Eulerian strain measures are
Another
strain measure can be defined as
This
can be computed directly from the deformation gradient as
and
is very similar to the Lagrangean strain tensor, except that its principal
directions are rotated through the rigid rotation R.
4.15 The
velocity gradient
We
now list several measures of the rate of
deformation. The velocity gradient is the basic measure of deformation rate,
and is defined as
It quantifies the relative velocities of two material
particles at positions y and y+dy in the deformed solid, in the sense
that
The velocity gradient can be expressed in terms of the
deformation gradient and its time derivative as
To see this, note that
and recall that ,
so that
4.16 Stretch
rate and spin tensors
The
stretch rate tensor is defined as
The
spin tensor is defined as
A
general velocity gradient can be decomposed into the sum of stretch rate and spin,
as
The
stretch rate quantifies the rate of stretching of material fibers in the
deformed solid, in the sense that
is
the rate of stretching of a material fiber with length l and orientation n in
the deformed solid. To see this, let ,
so that
By definition,
Hence
Finally,
take the dot product of both sides with n,
note that since n is a unit vector must be perpendicular to n and therefore . Note also that ,
since W is skew-symmetric. It is easiest to show this using index
notation: . Therefore
The
spin tensor W can be shown to
provide a measure of the average angular velocity of all material fibers
passing through a material point.
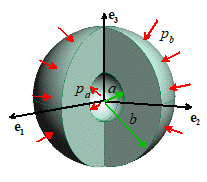 Example: a spherical shell (see the figure) is made from an incompressible
material. In its undeformed state, the
inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation
Example: a spherical shell (see the figure) is made from an incompressible
material. In its undeformed state, the
inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation
Recall
(see the example in Section 4.13) that the deformation gradient is
The
inverse of the deformation gradient (challenge can you show this?) is
Suppose
that the shell is continuously expanding (visualize a balloon being
inflated). The rate of expansion can be
characterized by the velocity of the surface that lies at R=A in the undeformed cylinder.
(a) Calculate the velocity field in the sphere as a function of
We have that
Hence
(b) Calculate the velocity field as a function of
(c) Calculate the time derivative of the deformation
gradient tensor
(d) Calculate the components of the velocity gradient by differentiating the result of (b)
(e) Calculate the components of the velocity gradient
using the results of (c) and the inverse of the deformation gradient
The other approach is to use
(f) Calculate the stretch rate tensor . Verify that the result represents a volume
preserving stretch rate field.
The stretch rate is the
symmetric part of - but it is symmetric anyway. So
To be volume preserving, . It is easy to show that this is indeed
satisfied.
4.17 Infinitesimal strain rate and rotation rate
For
small strains the rate of deformation
tensor can be approximated by the infinitesimal strain rate, while the spin can
be approximated by the time derivative of the infinitesimal rotation tensor
Similarly, you can show that
4.18 Other
deformation rate measures
The rate of deformation tensor can be related to time derivatives
of other strain measures. For example
the time derivative of the Lagrange strain tensor can be shown to be
Other useful results are
 For a
pure rotation ,
or equivalently . To see this, recall that and evaluate the time derivative.
For a
pure rotation ,
or equivalently . To see this, recall that and evaluate the time derivative.
 If the
deformation gradient is decomposed into a stretch followed by a rotation as then and
If the
deformation gradient is decomposed into a stretch followed by a rotation as then and
 . The trace of D is therefore a measure of rate of
change of volume.
. The trace of D is therefore a measure of rate of
change of volume.
For small strains the rate of change of
Lagrangian strain E is approximately equal to the rate of change
of infinitesimal strain :
4.19
Strain Equations of Compatibility for infinitesimal strains
It
is sometimes necessary to invert the
relations between strain and displacement that is to say, given the strain field, to
compute the displacements. In this section, we outline how this is done, for
the special case of infinitesimal
deformations.
For infinitesimal motions the
relation between strain and displacement is
Given
the six strain componets (six, since ) we wish to determine the three displacement
components .
First, note that you can never completely recover the displacement field that
gives rise to a particular strain field.
Any rigid motion produces no strain, so the displacements can only be
completely determined if there is some additional information (besides the
strain) that will tell you how much the solid has rotated and translated. However, integrating the strain field can
tell you the displacement field to within an arbitrary rigid motion.
Second,
we need to be sure that the strain-displacement relations can be integrated at
all. The strain is a symmetric second
order tensor field, but not all symmetric second order tensor fields can be
strain fields. The strain-displacement relations amount to a system of six
scalar differential equations for the three displacement components ui.
To be integrable, the strains
must satisfy the compatibility
conditions, which may be expressed as
Or, equivalently
Or, once more equivalently
It
is easy to show that all strain fields must satisfy these conditions - you simply need to substitute for the strains
in terms of displacements and show that the appropriate equation is
satisfied. For example,
and similarly for the other
expressions.
Not that for planar
problems for which all of these compatibilty equations are
satisfied trivially, with the exception of the first:
It
can be shown that
(i) If the
strains do not satisfy the equations of compatibility, then a displacement
vector can not be integrated from the strains.
(ii) If the strains satisfy the compatibility
equations, and the solid simply connected
(i.e. it contains no holes that go all the way through its thickness), then
a displacement vector can be integrated from the strains.
(iii) If the solid is not simply connected, a
displacement vector can be calculated, but it may not be single valued i.e. you may get different solutions depending
on how the path of integration encircles the holes.
Now,
let us return to the question posed at the beginning of this section. Given the strains, how do we compute the
displacements?
2D strain fields
For
2D (plane stress or plane strain) the procedure is quite simple and is best
illustrated by working through a specific case
As
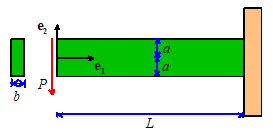
a representative example, we will use the strain field in a 2D (plane stress)
cantilever beam with Young’s modulus E
and Poisson’s ratio loaded at one end by a force P. The beam has a rectangular
cross-section with height 2a and
out-of-plane width b. We will show
later (Sect 5.2.4) that the strain field in the beam is
We first check that the
strain is compatible. For 2D problems
this requires
which is clearly satisfied
in this case.
For
a 2D problem we only need to determine and such that
.
The first two of these give
We
can integrate the first equation with respect to and the second equation with respect to to get
where
and are two functions of and ,
respectively, which are yet to be determined.
We can find these functions by substituting the formulas for and into the expression for shear strain
We can re-write this as
The
two terms in parentheses are functions of and ,
respectively. Since the left hand side
must vanish for all values of and ,
this means that
where is an arbitrary constant. We can now integrate these expressions to see
that
where c and d are two more
arbitrary constants. Finally, the displacement field follows as
The
three arbitrary constants ,
c and d can be seen to represent a small rigid rotation through angle about the axis, together with a displacement (c,d) parallel to axes, respectively.
 3D strain
fields
3D strain
fields
For
a general, three dimensional field a more formal procedure is required. Since
the strains are the derivatives of the displacement field, so you might guess
that we compute the displacements by integrating the strains. This is more or less correct. The general procedure is outlined below.
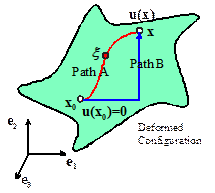
We
first pick a point in the solid, and arbitrarily say that the
displacement at is zero, and also take the rotation of the
solid at to be zero. Then, we can compute the displacements
at any other point x in the solid,
by integrating the strains along any convenient path. In a simply connected solid, it doesn’t
matter what path you pick.
Actually,
you don’t exactly integrate the strains instead, you must evaluate the following
integral
where
Here,
are the components of the position vector at
the point where we are computing the displacements, and are the components of the position vector of a point somewhere along the path of
integration. The fact that the integral is path-independent (in a simply
connected solid) is guaranteed by the compatibility condition. Evaluating this integral in practice can be
quite painful, but fortunately almost all cases where we need to integrate
strains to get displacement turn out to be two-dimensional.
 In this section, we list the various mathematical
formulas that are used to characterize shape changes in solids (and in
fluids). The formulas might look scary
at first, but they are mostly just definitions.
In this section, we list the various mathematical
formulas that are used to characterize shape changes in solids (and in
fluids). The formulas might look scary
at first, but they are mostly just definitions.
![]() Displacement
Gradient Tensor: is a tensor with components
Displacement
Gradient Tensor: is a tensor with components  The concepts of displacement gradient and deformation
gradient are introduced to quantify the change in shape of infinitesimal line
elements in a solid body. To see this, imagine drawing a straight line on the undeformed
configuration of a solid, as shown in the figure. The line would be mapped to a smooth curve on
the deformed configuration. However,
suppose we focus attention on a line segment dx, much shorter than the radius of curvature of this curve, as
shown. The segment would be straight in
the undeformed configuration, and would also be (almost) straight in the
deformed configuration. Thus, no matter
how complex a deformation we impose on a solid, infinitesimal line segments are
merely stretched and rotated by a deformation.The infinitesimal line segments dx and dy are related by
The concepts of displacement gradient and deformation
gradient are introduced to quantify the change in shape of infinitesimal line
elements in a solid body. To see this, imagine drawing a straight line on the undeformed
configuration of a solid, as shown in the figure. The line would be mapped to a smooth curve on
the deformed configuration. However,
suppose we focus attention on a line segment dx, much shorter than the radius of curvature of this curve, as
shown. The segment would be straight in
the undeformed configuration, and would also be (almost) straight in the
deformed configuration. Thus, no matter
how complex a deformation we impose on a solid, infinitesimal line segments are
merely stretched and rotated by a deformation.The infinitesimal line segments dx and dy are related by

![]() is the permutation
symbol. The element is mapped to a paralellepiped with sides dr,
dv, and dw
with volume given by
is the permutation
symbol. The element is mapped to a paralellepiped with sides dr,
dv, and dw
with volume given by![]() For any physically admissible deformation, the
volume of the deformed element must be positive (no matter how much you deform
a solid, you can’t make material disappear).
Therefore, all physically admissible displacement fields must satisfy J>0
For any physically admissible deformation, the
volume of the deformed element must be positive (no matter how much you deform
a solid, you can’t make material disappear).
Therefore, all physically admissible displacement fields must satisfy J>0![]() If a material is incompressible, its volume remains constant. This requires J=1.
If a material is incompressible, its volume remains constant. This requires J=1.![]() If the mass
density of the material at a point in the undeformed solid is , its mass density in the deformed solid
is
If the mass
density of the material at a point in the undeformed solid is , its mass density in the deformed solid
is  The Lagrange strain tensor is defined as
The Lagrange strain tensor is defined as![]() on our deforming
solid, as shown in the picture. The orientation of the specimen is arbitrary,
and is specified by a unit vector m,
with components . Upon deformation, the specimen increases in
length to .
Define the strain of the specimen as
on our deforming
solid, as shown in the picture. The orientation of the specimen is arbitrary,
and is specified by a unit vector m,
with components . Upon deformation, the specimen increases in
length to .
Define the strain of the specimen as
 Example 2: To track the
deformation in a slowly moving glacier, three survey stations are installed in
the shape of an equilateral triangle, spaced 100m apart, as shown in the
picture. After a suitable period of
time, the spacing between the three stations is measured again, and found to be
90m, 110m and 120m, as shown in the figure.
Assuming that the deformation of the glacier is homogeneous over the
region spanned by the survey stations, please compute the components of the
Lagrange strain tensor associated with this deformation, expressing your answer
as components in the basis shown.
Example 2: To track the
deformation in a slowly moving glacier, three survey stations are installed in
the shape of an equilateral triangle, spaced 100m apart, as shown in the
picture. After a suitable period of
time, the spacing between the three stations is measured again, and found to be
90m, 110m and 120m, as shown in the figure.
Assuming that the deformation of the glacier is homogeneous over the
region spanned by the survey stations, please compute the components of the
Lagrange strain tensor associated with this deformation, expressing your answer
as components in the basis shown.![]() For small strains, the engineering strain of
an infinitesimal fiber aligned with a unit vector m can be estimated as
For small strains, the engineering strain of
an infinitesimal fiber aligned with a unit vector m can be estimated as![]() Note that
Note that (see below for
more details)
(see below for
more details)![]() The infinitesimal strain tensor is closely
related to the strain matrix introduced in elementary strength of materials
courses. For example, the physical
significance of the (2 dimensional) strain matrix
The infinitesimal strain tensor is closely
related to the strain matrix introduced in elementary strength of materials
courses. For example, the physical
significance of the (2 dimensional) strain matrix![]() are
are




 The matrix V contains the three eigenvectors as
columns (they are not unit vectors). The
matrix D contains the principal strain values on the diagonals. The principal strain directions are therefore
at 45 degrees to the directions.
The deformation of a square element is illustrated in the figure below. The volume is constant; and the element is
stretched parallel to one principal direction, and compressed parallel to the
other.
The matrix V contains the three eigenvectors as
columns (they are not unit vectors). The
matrix D contains the principal strain values on the diagonals. The principal strain directions are therefore
at 45 degrees to the directions.
The deformation of a square element is illustrated in the figure below. The volume is constant; and the element is
stretched parallel to one principal direction, and compressed parallel to the
other. ![]() The
Right Cauchy Green Deformation Tensor
The
Right Cauchy Green Deformation Tensor ![]() The
Left Cauchy Green Deformation Tensor
The
Left Cauchy Green Deformation Tensor ![]() The
Right Stretch Tensor
The
Right Stretch Tensor ![]() The
Left Stretch Tensor
The
Left Stretch Tensor ![]() The
Rotation Tensor
The
Rotation Tensor 
 To visualize the physical significance of principal
stretches and their directions, note that a deformation can be decomposed as into a sequence of a stretch followed by a
rotation.
To visualize the physical significance of principal
stretches and their directions, note that a deformation can be decomposed as into a sequence of a stretch followed by a
rotation. 
 Example: a spherical shell (see the figure) is made from an
incompressible material. In its
undeformed state, the inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation
Example: a spherical shell (see the figure) is made from an
incompressible material. In its
undeformed state, the inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation Example: Repeat problem (a) from above, but this time
solve the problem using spherical-polar coordinates, using the various formulas
for vector and tensor operations given in Section 3.5 of the notes. In this case, you may assume that a point
with position in the undeformed solid has position vector
Example: Repeat problem (a) from above, but this time
solve the problem using spherical-polar coordinates, using the various formulas
for vector and tensor operations given in Section 3.5 of the notes. In this case, you may assume that a point
with position in the undeformed solid has position vector

 Example: a spherical shell (see the figure) is made from an incompressible
material. In its undeformed state, the
inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation
Example: a spherical shell (see the figure) is made from an incompressible
material. In its undeformed state, the
inner and outer radii of the shell are . After deformation, the new values are . The deformation in the shell can be described
(in Cartesian components) by the equation![]() For a
pure rotation ,
or equivalently . To see this, recall that and evaluate the time derivative.
For a
pure rotation ,
or equivalently . To see this, recall that and evaluate the time derivative. ![]() If the
deformation gradient is decomposed into a stretch followed by a rotation as then and
If the
deformation gradient is decomposed into a stretch followed by a rotation as then and ![]() . The trace of D is therefore a measure of rate of
change of volume.
. The trace of D is therefore a measure of rate of
change of volume.
 3D strain
fields
3D strain
fields



