Chapter 13

 

Plasticity

 

 

 

For many design calculations, the elastic constitutive equations outlined in Section 3.1 are sufficient, since large plastic strains are by and large undesirable and will lead to failure.  There are some applications, however, where it is of interest to predict the behavior of solids subjected to large loads, sufficient to cause permanent plastic strains.  Examples include:

 Modeling metal forming, machining or other manufacturing processes

 Designing crash resistant vehicles

 Plastic design of structures

 

Plasticity theory was developed to predict the behavior of metals under loads exceeding the plastic range, but the general framework of plasticity theory has since been adapted to other materials, including polymers and some types of soil (clay).  Some concepts from metal plasticity are also used in modeling concrete and other brittle materials such as polycrystalline ceramics.

 

 

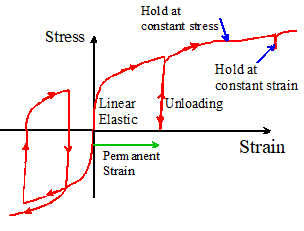
13.1 Features of the inelastic response of metals.

 

We begin by reviewing the results of a typical tension/compression test on an annealed, ductile, polycrystalline metal specimen (e.g. copper or Al).  Assume that the test is conducted at moderate temperature (less than $\mathrm{½}$ the melting point of the solid $–$ e.g. room temperature) and at modest strains (less than 10%), at modest strain rates ( ${10}^1-{10}^{-2}{\text{s}}^{\text{-1}}$ ).

 

The results of such a test are

 For modest stresses (and strains) the solid responds elastically.  This means the stress is proportional to the strain, and the deformation is reversible.

 If the stress exceeds a critical magnitude, the stress$—$strain curve ceases to be linear.  It is often difficult to identify the critical stress accurately, because the stress strain curve starts to curve rather gradually.

 If the critical stress is exceeded, the specimen is permanently changed in length on unloading.

 If the stress is removed from the specimen during a test, the stress$—$strain curve during unloading has a slope equal to that of the elastic part of the stress$—$strain curve.  If the specimen is re-loaded, it will initially follow the same curve, until the stress approaches its maximum value during prior loading.  At this point, the stress$—$strain curve once again ceases to be linear, and the specimen is permanently deformed further.

 If the test is interrupted and the specimen is held at constant strain for a period of time, the stress will relax slowly.  If the straining is resumed, the specimen will behave as though the solid were unloaded elastically.  Similarly, if the specimen is subjected to a constant stress, it will generally continue to deform plastically, although the plastic strain increases very slowly.  This phenomenon is known as `creep.’

 If the specimen is deformed in compression, the stress$—$strain curve is a mirror image of the tensile stress$—$strain curve (of course, this is only true for modest strains.  For large strains, geometry changes will cause differences between the tension and compression tests).

 If the specimen is first deformed in compression, then loaded in tension, it will generally start to deform plastically at a lower tensile stress than an annealed specimen.  This phenomenon is known as the `Bauschinger effect.’

 Material response to cyclic loading can be extremely complex.  One example is shown in the picture above $–$ in this case, the material hardens cyclically.  Other materials may soften.

 The detailed shape of the plastic stress$—$strain curve depends on the rate of loading, and also on temperature.

 

We also need to characterize the multi-axial response of an inelastic solid.  This is a much more difficult experiment to do.  Some of the nicest experiments were done by G.I. Taylor and collaborators in the early part of the last century.  Their approach was to measure the response of thin-walled tubes under combined torsion, axial loading and hydrostatic pressure. 

 

The main conclusions of these tests were

 The shape of the uniaxial stress-strain curve is insensitive to hydrostatic pressure.  However, the ductility (strain to failure) can be increased by adding hydrostatic pressure, particularly under torsional loading.

 Plastic strains are volume preserving, i.e. the plastic strain rate must satisfy  ${\dot{\epsilon }}_{kk}=0$

 During plastic loading, the principal components of the plastic strain rate tensor are parallel to the components of stress acting on the solid.  This sounds obvious until you think about it…  To understand what this means, imagine that you take a cylindrical shaft and pull it until it starts to deform plastically.  Then, holding the axial stress fixed, apply a torque to the shaft.  Experiments show that the shaft will initially stretch, rather than rotate.  The plastic strain increment is proportional to the stress acting on the shaft, not the stress increment.  This is totally unlike elastic deformation.

 Under multi-axial loading, most annealed polycrystalline solids obey the Levy-Mises flow rule, which relates the principal components of strain rate during plastic loading to the principal stresses as follows

$\frac{{\dot{\epsilon }}_1-{\dot{\epsilon }}_2}{{\sigma }_1-{\sigma }_2}=\frac{{\dot{\epsilon }}_1-{\dot{\epsilon }}_3}{{\sigma }_1-{\sigma }_3}=\frac{{\dot{\epsilon }}_2-{\dot{\epsilon }}_3}{{\sigma }_2-{\sigma }_3}$

 

In this section, we will outline the simplest plastic constitutive equations that capture the most important features of metal plasticity.  There are many different plastic constitutive laws, which are intended to be used in different applications.   There are two broad classes:

1.      Rate independent plasticity $–$ which is used to model metals deformed at low temperatures (less than half the material’s melting point) and modest strain rates (of order 0.01-10/s).  This is the focus of this section.

2.      Rate dependent plasticity, or viscoplasticity $–$ used to model high temperature creep (steady accumulation of plastic strain at contstant stress) and also to model metals deformed at high strain rates (100/s or greater), where flow strength is sensitive to deformation rate.   

 

There are also various different models within these two broad categories.   The models generally differ in two respects (i) the yield criterion; (ii) the strain hardening law.  There is no completely general model that describes all the features that were just listed, so in any application, you will need to decide which aspect of material behavior is most important, and then choose a model that accurately characterizes this behavior.

 

 

Key ideas in modeling metal plasticity

 

Five key concepts form the basis of almost all classical theories of plasticity.  They are

1.      The decomposition of strain into elastic and plastic parts;

2.      Yield criteria, which predict whether the solid responds elastically or plastically;

3.      Strain hardening rules, which control the way in which resistance to plastic flow increases with plastic straining;

4.      The plastic flow rule, which determines the relationship between stress and plastic strain under multi-axial loading;

5.      The elastic unloading criterion, which models the irreversible behavior of the solid.

These concepts will be described in more detail in the sections below.

 

For simplicity, we will at this stage restrict attention to infinitesimal deformations.

 

Consequently, we adopt the infinitesimal strain tensor

${\epsilon }_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$

as our deformation measure.  We have no need to distinguish between the various stress measures and will use ${\sigma }_{ij}$ to denote stress.

 

It is also important to note that the plastic strains in a solid depend on the load history.  This means that the stress-strain laws are not just simple equations relating stress to strain.  Instead, plastic strain laws must either relate the strain rate in the solid to the stress and stress rate, or else specify the relationship between a small increment of plastic strain $d{\epsilon }_{ij}^p$ in terms of strain, stress and stress increment $d{\sigma }_{ij}$.  In addition, plasticity problems are almost always solved using the finite element method.  Consequently, numerical methods are used to integrate the plastic stress-strain equations.

 

 

 

13.2. Decomposition of strain into elastic and plastic parts

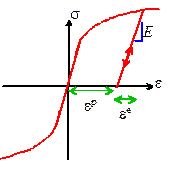
Experiments show that under uniaxial loading, the strain at a given stress has two parts: a small recoverable elastic strain, and a large, irreversible plastic strain, as shown in the picture.  In uniaxial tension, we would write

$\epsilon ={\epsilon }^e+{\epsilon }^p$

Experiments suggest that the reversible part is related to the stress through the usual linear elastic equations.   Plasticity theory is concerned with characterizing the irreversible part.

 

For multiaxial loading, we generalize this by decomposing a general strain increment $d{\epsilon }_{ij}$ into elastic and plastic parts (as well as an optional thermal expansion), as

$d{\epsilon }_{ij}=d{\epsilon }_{ij}^e+d{\epsilon }_{ij}^p+d{\epsilon }_{ij}^T$

The elastic part of the strain is related to stress using the linear elastic equations

$d{\epsilon }_{ij}^e=\frac{1+\nu }{E}d{\sigma }_{ij}-\frac{\nu }{E}d{\sigma }_{kk}{\delta }_{ij}$

The thermal strain is

$d{\epsilon }_{ij}^T=\alpha dT{\delta }_{ij}$ 

 

 

 

13.3 Yield Criteria

 

The yield criterion is used to determine the critical stress required to cause permanent deformation in a material.  There are many different yield criteria $–$ here we will just list the simplest ones.  Let ${\sigma }_{ij}$ be the stress acting on a solid, and let ${\sigma }_1,{\sigma }_2,{\sigma }_3$ denote the principal values of stress.  In addition, let $Y$ denote the yield stress of the material in uniaxial tension.  Then, define

 Von$—$Mises yield criterion

$f\left({\sigma }_{ij},{\overline{\epsilon }}^p\right)=\sqrt{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2\right]}-Y\left({\overline{\epsilon }}^p\right)=0$

 

 Tresca yield criterion

$f\left({\sigma }_{ij},{\overline{\epsilon }}^p\right)=\max \left\{\left|{\sigma }_1-{\sigma }_2\right|,\left|{\sigma }_1-{\sigma }_3\right|,\left|{\sigma }_2-{\sigma }_3\right|\right\}-Y\left({\overline{\epsilon }}^p\right)=0$

In both cases, the criteria are defined so that the material deforms elastically for $f\left({\sigma }_{ij}\right)<0$, and plastically for $f\left({\sigma }_{ij}\right)=0$.  The yield stress $Y$ may increase during plastic straining, so we have shown that Y is a function of a measure of total plastic strain ${\overline{\epsilon }}^p$, to be defined in below.

 

 An alternative form of Von$—$Mises criterion. For a general stress state, it is a nuisance having to compute the principal stresses in order to apply von Mises yield criterion.  Fortunately, the criterion can be expressed directly in terms of the stress tensor

$f\left({\sigma }_{ij},{\overline{\epsilon }}^p\right)={\sigma }_e-Y\left({\overline{\epsilon }}^p\right)$

where

${\sigma }_e=\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}{S}_{ij}={\sigma }_{ij}-\frac{1}{3}{\sigma }_{kk}{\delta }_{ij}$

are the components of the `von Mises effective stress’ and  `deviatoric stress tensor’ respectively.

 

These yield criteria are based largely on the following experimental observations:

(1)  A hydrostatic stress (all principal stresses equal) will never cause yield, no matter how large the stress;

(2) Most polycrystalline metals are isotropic.  Since the yield criterion depends only on the magnitudes of the principal stresses, and not their directions, the yield criteria predict isotropic behavior.

 

Tests suggest that von Mises yield criterion provides a slightly better fit to experiment than Tresca, but the difference between them is very small.   Sometimes it simplifies calculations to use Tresca’s criterion instead of von Mises.

 

 

 

13.4 Graphical representation of the yield surface.

 

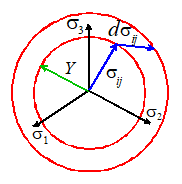
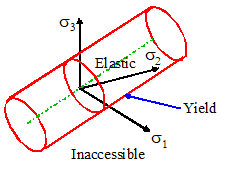Any arbitrary stress state can be plotted in  `principal stress space,’ with the three principal stresses as axes.

 

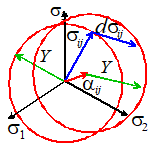
The Von$—$Mises yield criterion is plotted in this way in the picture to the right.  The yield criterion is a cylinder, radius $Y/\sqrt{3}$, with its axis parallel to the line

${\sigma }_1={\sigma }_2={\sigma }_3$

If the state of stress falls within the cylinder, the material is below yield and responds elastically.  If the state of stress lies on the surface of the cylinder, the material yields and deforms plastically.  If the plastic deformation causes the material to strain harden, the radius of the cylinder increases.  The stress state cannot lie outside the cylinder $–$ this would lead to an infinite plastic strain.

 

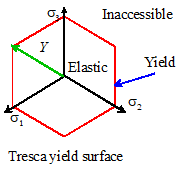
Because the yield criterion $f({\sigma }_{ij})=0$ defines a surface in stress space, it is often referred to as a yield surface. The yield surface is often drawn as it would appear when viewed down the axis of the cylinder, as shown below. The Tresca yield criterion can also be plotted in this way.  It looks like a cylinder with a hexagonal cross section, as shown.

        

 

 

13.5. Strain hardening laws

 

Experiments show that if you plastically deform a solid, then unload it, and then try to re-load it so as to induce further plastic flow, its resistance to plastic flow will have increased.  This is known as strain hardening.

 

Obviously, we can model strain hardening by relating the size and shape of the yield surface to plastic strain in some appropriate way.  There are many ways to do this.  Here we describe the two simplest approaches.

 

 Isotropic hardening

Rather obviously, the easiest way to model strain hardening is to make the yield surface increase in size, but remain the same shape, as a result of plastic straining.

 

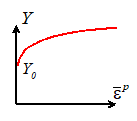
This means we must devise some appropriate relationship between Y and the plastic strain.  To get a suitable scalar measure of plastic strain we define the accumulated plastic strain magnitude

${\overline{\epsilon }}^p={\displaystyle \int \sqrt{\frac{2}{3}d{\epsilon }_{ij}^{p}d{\epsilon }_{ij}^p}}$

(the factor of 2/3 is introduced so that ${\overline{\epsilon }}^p={\epsilon }_{11}^p$ in a uniaxial tensile test in which the specimen is stretched parallel to the $e_1$ direction.  To see this, note that plastic strains do not change volume, so that $d{\epsilon }_{22}=d{\epsilon }_{33}=-d{\epsilon }_{11}/2$ and substitute into the formula.)

 

Then we make Y a function of ${\overline{\epsilon }}^p$.  People often use power laws or piecewise linear approximations in practice. A few of the more common forms of hardening functions are

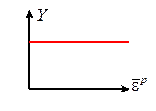
Perfectly plastic solid:  $Y=\text{constant}$

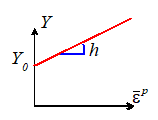
Linear strain hardening solid: $Y\left({\overline{\epsilon }}^p\right)=Y_0+h{\overline{\epsilon }}^p$

Power$—$law hardening material: $Y=Y_0+h{\left({\overline{\epsilon }}^p\right)}^{1/m}$

In these formulas, 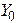, h and m are material properties.  These functions are illustrated in the figures below

 

 

     

 Kinematic hardening

 

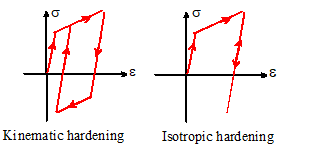
An isotropic hardening law is generally not useful in situations where components are subjected to cyclic loading.  It does not account for the Bauschinger effect, and so predicts that after a few cycles the solid will just harden until it responds elastically.

 

To fix this, an alternative hardening law allows the yield surface to translate, without changing its shape.  The idea is illustrated graphically in the picture.  As you deform the material in tension, you drag the yield surface in the direction of increasing stress, thus modeling strain hardening.  This softens the material in compression, however.  So, this constitutive law can model cyclic plastic deformation.  The stress-strain curves for isotropic and kinematic hardening materials are contrasted in the figure on the right.

 

To account for the fact that the center of the yield locus is at a position ${\alpha }_{ij}$ in stress space, the Von-Mises yield criterion needs to be modified as follows

$f({\sigma }_{ij},{\alpha }_{ij})=\sqrt{\frac{3}{2}\left(S_{ij}-{\alpha }_{ij}\right)\left(S_{ij}-{\alpha }_{ij}\right)}-Y=0$

Here, Y is now a constant, and hardening is modeled by the motion of the yield surface. To do so, we need to relate ${\alpha }_{ij}$ to the plastic strain history somehow.  There are many ways to do this, which can model subtle features of the plastic response of solids under cyclic and nonproportional loading. The simplest approach is to set

$d{\alpha }_{ij}=\frac{2}{3}cd{\epsilon }_{ij}^p$.

 This hardening law predicts that the stress-plastic strain curve is a straight line with slope c.  This is known as linear kinematic hardening. 

 

 

A more sophisticated approach is to set

$d{\alpha }_{ij}=\frac{2}{3}cd{\epsilon }_{ij}^p-\gamma {\alpha }_{ij}d{\overline{\epsilon }}^p$

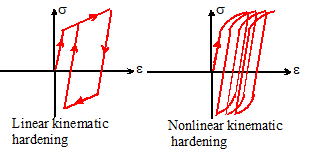
where c and $\gamma$ are material constants.  It’s not so easy to visualize what this does $–$ it turns out that that this relation can model cyclic creep $–$ the tendency of a material to accumulate strain in the direction of mean stress under cyclic loading, as illustrated in the figure on the right.  It is known as the Armstrong-Frederick hardening law.

 

There are many other kinematic type hardening laws.  New ones are still being developed. 

 

 

 

13.6 The plastic flow law

 

To complete the plastic stress-strain relations, we need a way to predict the plastic strains induced by stressing the material beyond the yield point.  Specifically, given

1.      The current stress ${\sigma }_{ij}$ applied to the material

2.      The current yield stress (characterized by $Y({\overline{\epsilon }}^p)$ for isotropic hardening, or ${\alpha }_{ij}$ for kinematic hardening)

3.      A small increase in stress $d{\sigma }_{ij}$ applied to the solid

we wish to determine the small change in plastic strain $d{\epsilon }_{ij}^p$.

 

The formulas are given below, for isotropic and kinematic hardening.  These are just fits to experiment (specifically, to the Levy-Mises flow rule).  The physical significance and reason for the structure of the equations will be discussed later.

 

The plastic strains are usually derived from the yield criterion f defined in 3.6.3, and so are slightly different for isotropic and kinematic hardening.  A material that has its plastic flow law derived from f is said to have an `associated’ flow law $–$ i.e.the flow law is associated with f.

 

 

Isotropic Hardening (Von-Mises yield criterion)

$d{\epsilon }_{ij}^p=d{\overline{\epsilon }}^p\frac{\partial f}{\partial {\sigma }_{ij}}=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{ij}}{Y}$

where

$f\left({\sigma }_{ij},{\overline{\epsilon }}^p\right)=\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y\left({\overline{\epsilon }}^p\right)S_{ij}={\sigma }_{ij}-\frac{1}{3}{\sigma }_{kk}{\delta }_{ij}$

denotes the Von-Mises yield criterion, and $d{\overline{\epsilon }}^p$ is determined from the condition that the yield criterion must be satisfied at all times during plastic straining.  This shows that

$\begin{array}{l}f({\sigma }_{ij}+d{\sigma }_{ij},{\overline{\epsilon }}^p+d{\overline{\epsilon }}^p)=f({\sigma }_{ij},{\overline{\epsilon }}^p)+\frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}+\frac{\partial f}{\partial {\overline{\epsilon }}^p}d{\overline{\epsilon }}^p=0\\ \Rightarrow \frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}-\frac{\partial Y}{\partial {\overline{\epsilon }}^p}d{\overline{\epsilon }}^p=0\\ \Rightarrow d{\overline{\epsilon }}^p=\frac{1}{h}\frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}=\frac{1}{h}\frac{3}{2}\frac{S_{ij}d{\sigma }_{ij}}{Y}h=\frac{dY}{d{\overline{\epsilon }}^p}\end{array}$

Here, $h=\partial Y/\partial {\overline{\epsilon }}^p$ is the slope of the plastic stress-strain curve.   The algebra involved in differentiating f with respect to stress is outlined below.

 

 

Linear Kinematic Hardening (Von-Mises yield criterion)

$d{\epsilon }_{ij}^p=d{\overline{\epsilon }}^p\frac{\partial f}{\partial {\sigma }_{ij}}=d{\overline{\epsilon }}^p\frac{3}{2}\frac{\left(S_{ij}-{\alpha }_{ij}\right)}{Y}$

where the yield criterion is now

$f\left({\sigma }_{ij},{\alpha }_{ij}\right)=\sqrt{\frac{3}{2}\left(S_{ij}-{\alpha }_{ij}\right)\left(S_{ij}-{\alpha }_{ij}\right)}-Y{S}_{ij}={\sigma }_{ij}-\frac{1}{3}{\sigma }_{kk}{\delta }_{ij}$

and as before $d{\overline{\epsilon }}^p$ is determined from the condition that the yield criterion must be satisfied at all times during plastic straining.  This shows that

$f({\sigma }_{ij}+d{\sigma }_{ij},{\alpha }_{ij}+d{\alpha }_{ij})=f({\sigma }_{ij},{\alpha }_{ij})+\frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}+\frac{\partial f}{\partial {\alpha }_{ij}}d{\alpha }_{ij}=0$

Recall that for linear kinematic hardening the hardening law is

$d{\alpha }_{ij}=\frac{2}{3}cd{\epsilon }_{ij}^p=cd{\overline{\epsilon }}^p\frac{\left(S_{ij}-{\alpha }_{ij}\right)}{Y}$

Substituting into the Taylor expansion of the yield criterion and simplifying shows that

$d{\overline{\epsilon }}^p=\frac{1}{c}\frac{3}{2}\frac{\left(S_{ij}-{\alpha }_{ij}\right)d{\sigma }_{ij}}{Y}$

 

 

 

Comparison of flow law formulas with the Levy-Mises flow rule

 

The Levy-Mises flow law (based on experimental observations) states that principal values of the plastic strain increment $d{\epsilon }_1,d{\epsilon }_2,d{\epsilon }_3$ induced by a stress increment are related to the principal stresses ${\sigma }_1,{\sigma }_2,{\sigma }_3$ by

$\frac{d{\epsilon }_1-d{\epsilon }_2}{{\sigma }_1-{\sigma }_2}=\frac{d{\epsilon }_1-d{\epsilon }_3}{{\sigma }_1-{\sigma }_3}=\frac{d{\epsilon }_2-d{\epsilon }_3}{{\sigma }_2-{\sigma }_3}$

It is straightforward to show that this observation is consistent with the predictions of the flow law formulas given in this section. To see this, suppose that the principal axes of stress are parallel to the $\{e_1,e_2,e_3\}$ directions.  In this case the only nonzero components of deviatoric stress are

$S_{11}={\sigma }_1-({\sigma }_1+{\sigma }_2+{\sigma }_3)/3S_{22}={\sigma }_2-({\sigma }_1+{\sigma }_2+{\sigma }_3)/3S_{33}={\sigma }_1-({\sigma }_1+{\sigma }_2+{\sigma }_3)/3$

 

 

The flow law

$d{\epsilon }_{ij}^p=d{\overline{\epsilon }}^p\frac{\partial f}{\partial {\sigma }_{ij}}=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{ij}}{Y}$ 

gives

$d{\epsilon }_1^p=d{\epsilon }_{11}^p=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{11}}{Y}d{\epsilon }_2^p=d{\epsilon }_{22}^p=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{22}}{Y}d{\epsilon }_3^p=d{\epsilon }_{33}^p=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{33}}{Y}$

Thus, we see that

$\begin{array}{l}d{\epsilon }_1^p-d{\epsilon }_2^p=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{11}-S_{22}}{Y}=d{\overline{\epsilon }}^p\frac{3}{2}\frac{{\sigma }_1-{\sigma }_2}{Y}\\ d{\epsilon }_1^p-d{\epsilon }_3^p=d{\overline{\epsilon }}^p\frac{3}{2}\frac{S_{11}-S_{33}}{Y}=d{\overline{\epsilon }}^p\frac{3}{2}\frac{{\sigma }_1-{\sigma }_3}{Y}\end{array}$

with similar expressions for other components.  Some trivial algebra then yields the Levy-Mises flow law.

 

 

Differentiating the yield criterion

 

Differentiating the yield criterion requires some sneaky index notation manipulations. Note that

$\frac{\partial f}{\partial {\sigma }_{ij}}=\frac{3}{2}\frac{1}{2}\frac{1}{\sqrt{\frac{3}{2}{S}_{kl}{S}_{kl}}}2S_{pq}\frac{\partial S_{pq}}{\partial {\sigma }_{ij}}=\frac{3}{2}\frac{1}{\sqrt{\frac{3}{2}{S}_{kl}{S}_{kl}}}{S}_{pq}\frac{\partial S_{pq}}{\partial {\sigma }_{ij}}$

Now, recall that

$S_{ij}={\sigma }_{ij}-\frac{1}{3}{\sigma }_{kk}{\delta }_{ij}$

and further that

$\frac{\partial {\sigma }_{ij}}{\partial {\sigma }_{kl}}={\delta }_{ik}{\delta }_{jl}$

Hence

$\frac{\partial S_{pq}}{\partial {\sigma }_{ij}}={\delta }_{ip}{\delta }_{jq}-\frac{1}{3}{\delta }_{ik}{\delta }_{jk}{\delta }_{pq}$

and

$S_{pq}\frac{\partial S_{pq}}{\partial {\sigma }_{ij}}=S_{pq}\left({\delta }_{ip}{\delta }_{jq}-\frac{1}{3}{\delta }_{ik}{\delta }_{jk}{\delta }_{pq}\right)=S_{ij}-S_{pp}{\delta }_{ij}$

However, observe that

$S_{pp}={\sigma }_{pp}-\frac{1}{3}{\sigma }_{kk}{\delta }_{pp}=0$

so that

$S_{pq}\frac{\partial S_{pq}}{\partial {\sigma }_{ij}}=S_{ij}$

and finally

$\frac{\partial f}{\partial {\sigma }_{ij}}=\frac{3}{2}\frac{S_{ij}}{\sqrt{\frac{3}{2}{S}_{kl}{S}_{kl}}}=\frac{3}{2}\frac{S_{ij}}{Y}$

 

13.7 The Elastic unloading condition

 

There is one final issue to consider.  Experiments show that plastic flow is irreversible, and always dissipates energy.  If the increment in stress $d{\sigma }_{ij}$ is tangent to the yield surface, or brings the stress below yield, as shown in the picture then there is no plastic strain.

 

For an isotropically hardening solid, this unloading condition may be expressed as

$S_{ij}d{\sigma }_{ij}^{}<0$

For kinematic hardening,

$\left(S_{ij}-{\alpha }_{ij}\right)d{\sigma }_{ij}^{}<0$

In both cases, the solid deforms elastically (no plastic strain) if the condition is satisfied.

 

 

 

13.8 Complete incremental stress-strain relations for a rate independent elastic-plastic solid

 

We conclude by summarizing the complete elastic-plastic stress strain relations for an isotropic  solid with Von-Mises yield surface. 

 

 

Isotropically hardening elastic-plastic solid

 

The solid is characterized by its elastic constants $E,\nu$ and by the yield stress $Y({\overline{\epsilon }}^p)$ as a function of accumulated plastic strain ${\overline{\epsilon }}^p$ and its slope $h=\frac{dY}{d{\overline{\epsilon }}^p}$ 

 

In this case we have that

$d{\epsilon }_{ij}=d{\epsilon }_{ij}^e+d{\epsilon }_{ij}^p$

with

$d{\epsilon }_{ij}^e=\frac{1+\nu }{E}\left(d{\sigma }_{ij}-\frac{\nu }{1+\nu }d{\sigma }_{kk}{\delta }_{ij}\right)$

$d{\epsilon }_{ij}^p=\{\begin{array}{c}0\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y({\overline{\epsilon }}^p)<0\\ \frac{1}{h}\frac{3}{2}\frac{\langle S_{kl}d{\sigma }_{kl}\rangle }{Y}\frac{3}{2}\frac{S_{ij}}{Y}\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y({\overline{\epsilon }}^p)=0\end{array}$

where $\langle x\rangle =\{\begin{array}{c}xx\ge 0\\ 0x\le 0\end{array}$

 

 

 

 

 

These may be combined to

$d{\epsilon }_{ij}^{}=\{\begin{array}{c}\frac{1+\nu }{E}\left(d{\sigma }_{ij}-\frac{\nu }{1+\nu }d{\sigma }_{kk}{\delta }_{ij}\right)\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y({\overline{\epsilon }}^p)<0\\ \frac{1+\nu }{E}\left(d{\sigma }_{ij}-\frac{\nu }{1+\nu }d{\sigma }_{kk}{\delta }_{ij}\right)+\frac{1}{h}\frac{3}{2}\frac{\langle S_{kl}d{\sigma }_{kl}\rangle }{Y}\frac{3}{2}\frac{S_{ij}}{Y}\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y({\overline{\epsilon }}^p)=0\end{array}$

It is sometimes necessary to invert these expressions.  A straightforward but tedious series of index notation manipulations shows that

$d{\sigma }_{ij}=\{\begin{array}{c}\frac{E}{1+\nu }\left\{d{\epsilon }_{ij}+\frac{\nu }{1-2\nu }d{\epsilon }_{kk}{\delta }_{ij}\right\}\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y({\overline{\epsilon }}^p)<0\\ \frac{E}{1+\nu }\left\{d{\epsilon }_{ij}+\frac{\nu }{1-2\nu }d{\epsilon }_{kk}{\delta }_{ij}-\frac{3E}{3E+2(1+\nu )h}\frac{3}{2}\frac{\langle S_{kl}d{\epsilon }_{kl}\rangle }{Y}\frac{3}{2}\frac{S_{ij}}{Y}\right\}\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}-Y({\overline{\epsilon }}^p)=0\end{array}$

 

This constitutive law is the most commonly used model of inelastic deformation.  It has the following properties:

 It will correctly predict the conditions necessary to initiate yield under multiaxial loading

 It will correctly predict the plastic strain rate under an arbitrary multiaxial stress state

 It can model accurately any uniaxial stress$—$strain curve

 

It has the following limitations:

 It is valid only for modest plastic strains (<10%)

 It will not predict creep behavior or strain rate sensitivity

 It does not predict behavior under cyclic loading correctly

 It will not predict plastic strains accurately if the principal axes of stress rotate significantly (more than about 30 degrees) during inelastic deformation

 

Linear Kinematically hardening solid

 

The solid is characterized by its elastic constants $E,\nu$ and by the initial yield stress $Y$ and the strain hardening rate c. Then,

$d{\epsilon }_{ij}=d{\epsilon }_{ij}^e+d{\epsilon }_{ij}^p$

with

$d{\epsilon }_{ij}^e=\frac{1+\nu }{E}\left(d{\sigma }_{ij}-\frac{\nu }{1+\nu }d{\sigma }_{kk}{\delta }_{ij}\right)$

$d{\epsilon }_{ij}^p=\{\begin{array}{c}0\sqrt{\frac{3}{2}\left(S_{ij}-{\alpha }_{ij}\right)\left(S_{ij}-{\alpha }_{ij}\right)}-Y<0\\ \frac{1}{c}\frac{3}{2}\frac{\langle \left(S_{kl}-{\alpha }_{kl}\right)d{\sigma }_{kl}\rangle }{Y}\frac{3}{2}\frac{\left(S_{ij}-{\alpha }_{ij}\right)}{Y}\sqrt{\frac{3}{2}\left(S_{ij}-{\alpha }_{ij}\right)\left(S_{ij}-{\alpha }_{ij}\right)}-Y=0\end{array}$

where $\langle x\rangle =\{\begin{array}{c}xx\ge 0\\ 0x\le 0\end{array}$

Finally, the evolution equation for ${\alpha }_{ij}$ is

$d{\alpha }_{ij}=\frac{3}{2}cd{\epsilon }_{ij}^p$

 

This constitutive equation is used primarily to model cyclic plastic deformation, or plastic flow under nonproportional loading (where principal axes of stress rotate significantly during plastic flow). It has the following limitations:

 It is valid only for modest plastic strains (<10%)

 It will not predict creep behavior or strain rate sensitivity

 It does not predict the shape of the stress-strain curve accurately

 

 

13.9 Typical values for yield stress of polycrystalline metals

 

Unlike elastic constants, the plastic properties of metals are highly variable, and are also very sensitive to alloying composition and microstructure (which can be influenced by heat treatment and mechanical working).  Consequently, it is impossible to give accurate values for yield stresses or hardening rates for materials.  The table below (again, taken from `Engineering Materials,’ by M.F. Ashby and D.R.H. Jones, Pergamon Press) lists rough values for yield stresses of common materials $–$ these may provide a useful guide in preliminary calculations.  If you need accurate data you will have to measure the properties of the materials you plan to use yourself.

Material	Yield Stress ${\sigma }_Y/MN{m}^{-2}$	Material	Yield Stress ${\sigma }_Y/MN{m}^{-2}$
Tungsten Carbide	6000	Mild steel	220
Silicon Carbide	10 000	Copper	60
Tungsten	2000	Titanium	180 - 1320
Alumina	5000	Silica glass	7200
Titanium Carbide	4000	Aluminum & alloys	40-200
Silicon Nitride	8000	Polyimides	52 - 90
Nickel	70	Nylon	49 - 87
Iron	50	PMMA	60 - 110
Low alloy steels	500-1980	Polycarbonate	55
Stainless steel	286-500	PVC	45-48

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

13.10 Thin walled tube under combined tension and torsion

 

It is usually difficult to solve boundary value problems for plastically deforming solids, because the stress-strain law is nonlinear, and history dependent.   Finite element calculations can handle both without difficulty.   But it is helpful to solve a few example problems for solids with simple geometries and loading to illustrate how the stress-strain laws work.

 

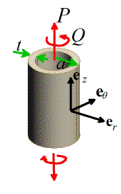
The figure shows a thin walled tube with cross-sectional area $A=2\pi at$ .   It is made from an elastic-plastic solid with elastic constants $E,\nu$ , yield stress Y and hardening slope $dY/d{\overline{\epsilon }}^p=h$ .   It is loaded by axial force P and torque Q.   Calculate the plastic strain rate in the tube.

 

1.      The stress in the tube is ${\sigma }_{zz}=P/A{\sigma }_{r\theta }={\sigma }_{\theta r}=Q/(aA)$ ; all other components zero.

2.      The hydrostatic stress is ${\sigma }_{kk}/3=P/(3A)$ 

3.      The deviatoric stresses follow as $S_{zz}=2P/(3A)S_{rr}=S_{\theta \theta }=-P/(3A)$ $S_{r\theta }=S_{\theta r}=Q/(aA)$

4.      The Von-Mises effective stress is therefore

${\sigma }_e=\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij}}=\sqrt{\frac{3}{2}\left[{\left(\frac{2P}{3A}\right)}^2+2{\left(\frac{P}{3A}\right)}^2+2{\left(\frac{Q}{aA}\right)}^2\right]}=\frac{1}{A}\sqrt{P^2+3{(Q/a)}^2}$

5.      We can use the sress-strain rate formulas to calculate the strain rate

 

$\frac{d{\epsilon }_{ij}^{}}{dt}=\{\begin{array}{c}\frac{1+\nu }{E}\left(\frac{d{\sigma }_{ij}}{dt}-\frac{\nu }{1+\nu }\frac{d{\sigma }_{kk}}{dt}{\delta }_{ij}\right){\sigma }_e-Y({\overline{\epsilon }}^p)<0\\ \frac{1+\nu }{E}\left(\frac{d{\sigma }_{ij}}{dt}-\frac{\nu }{1+\nu }\frac{d{\sigma }_{kk}}{dt}{\delta }_{ij}\right)+\frac{1}{h}\frac{3}{2}\frac{\langle S_{kl}\frac{d{\sigma }_{kl}}{dt}\rangle }{{\sigma }_e}\frac{3}{2}\frac{S_{ij}}{{\sigma }_e}{\sigma }_e-Y({\overline{\epsilon }}^p)=0\end{array}$

 

The quantity

$\langle S_{kl}\frac{d{\sigma }_{kl}}{dt}\rangle =\langle \frac{2P}{3A^2}\frac{dP}{dt}+2\frac{Q}{{(aA)}^2}\frac{dQ}{dt}\rangle$

 

$\frac{d{\epsilon }_{zz}^{}}{dt}=\{\begin{array}{c}\frac{1}{EA}\frac{dP}{dt}{\sigma }_e-Y({\overline{\epsilon }}^p)<0\\ \frac{1}{EA}\frac{dP}{dt}+\frac{P}{Ah}\frac{\langle P\frac{dP}{dt}+3\frac{Q}{{(a)}^2}\frac{dQ}{dt}\rangle }{\left[P^2+3{(Q/a)}^2\right]}{\sigma }_e-Y({\overline{\epsilon }}^p)=0\end{array}$

$\frac{d{\epsilon }_{rr}^{}}{dt}=\frac{d{\epsilon }_{\theta \theta }^{}}{dt}=\{\begin{array}{c}\frac{-\nu }{EA}\frac{dP}{dt}{\sigma }_e-Y({\overline{\epsilon }}^p)<0\\ \frac{-\nu }{EA}\frac{dP}{dt}-\frac{P}{2Ah}\frac{\langle P\frac{dP}{dt}+3\frac{Q}{{(a)}^2}\frac{dQ}{dt}\rangle }{\left[P^2+3{(Q/a)}^2\right]}{\sigma }_e-Y({\overline{\epsilon }}^p)=0\end{array}$

$\frac{d{\epsilon }_{z\theta }^{}}{dt}=\frac{d{\epsilon }_{\theta z}^{}}{dt}=\{\begin{array}{c}\frac{1+\nu }{EAa}\frac{dQ}{dt}{\sigma }_e-Y({\overline{\epsilon }}^p)<0\\ \frac{1+\nu }{EAa}\frac{dQ}{dt}+\frac{3Q}{2Aah}\frac{\langle P\frac{dP}{dt}+3\frac{Q}{{(a)}^2}\frac{dQ}{dt}\rangle }{\left[P^2+3{(Q/a)}^2\right]}{\sigma }_e-Y({\overline{\epsilon }}^p)=0\end{array}$

 

 

There are some surprising features of these results.   For example, notice that if the tube is first deformed by a force P, and is then twisted (so that $dP/dt=0dQ/dt>0$ ) the tube will experience an axial plastic stretch before it starts to twist.  This is because the direction of the plastic strain rate is parallel to the deviatoric stress, not the stress rate.     

 

 

 

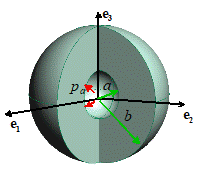13.11 Elastic-perfectly plastic hollow sphere subjected to monotonically increasing internal pressure

 

Assume that

 The sphere is stress free before it is loaded

 No body forces act on the sphere

 The sphere has uniform temperature

 The inner surface r=a is subjected to (monotonically increasing) pressure $p_a$

 The outer surface r=b is traction free

 Strains are infinitesimal

 

Solution:

 

(i) Preliminaries:

 The sphere first reaches yield (at r=a) at an internal pressure $p_a/Y=2(1-a^3/b^3)/3$

 For pressures in the range $2(1-a^3/b^3)/3<p_a/Y<2\log (b/a)$ the region between $r=a$ and $r=c$ deforms plastically; while the region between $c<r<b$ remains elastic, where c satisfies the equation $p_a/Y=2\log (c/a)+\frac{2}{3}(1-c^3/b^3)$

 At a pressure $p_a/Y=2\log (b/a)$ the entire cylinder is plastic.  At this point the sphere collapses $–$ the displacements become infinitely large.

 

(ii) Solution in the plastic region $a<r<c$

$u=\frac{\left(1-2\nu \right)}{E}r\left\{2Y\log (r/a)-p_a\right\}{e}_r+\frac{Y\left(1-\nu \right)c^3}{E{r}^2}{e}_r$

${\sigma }_{rr}=2Y\log (r/a)-p_a{\sigma }_{\theta \theta }={\sigma }_{\varphi \varphi }=2Y\log (r/a)-p_a+Y$    

(iii) Solution in the elastic region $c<r<b$

$u=\frac{Y{c}^3}{3E{b}^3{r}^2}\left\{2\left(1-2\nu \right)r^3+\left(1+\nu \right)b^3\right\}{e}_r$

${\sigma }_{rr}=\frac{2Y{c}^3}{3b^3}\left(1-\frac{b^3}{r^3}\right)$           ${\sigma }_{\theta \theta }={\sigma }_{\varphi \varphi }=\frac{2Y{c}^3}{3b^3}\left(1+\frac{b^3}{2r^3}\right)$

These results are plotted in the figures below.

 

  

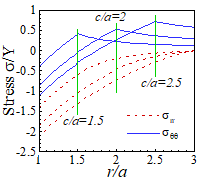
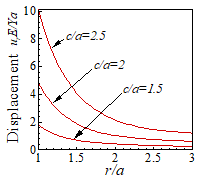
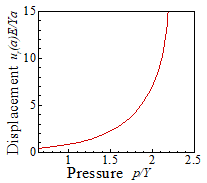
(a)                                                   (b)                                              (c)

(a) Stress and (b) displacement distributions for a pressurized elastic-perfectly plastic spherical shell; and (c) Displacement at r=a as a function of pressure. Displacements are shown for $\nu =0.3$

 

 

 

 

Derivation: By substituting the stresses for the elastic solution given in 4.1.4 into the Von-Mises yield criterion, we see that a pressurized elastic sphere first reaches yield at r=a. If the pressure is increased beyond yield we anticipate that a region $a<r<c$ will deform plastically, while a region $c<r<b$ remains elastic. We must find separate solutions in the plastic and elastic regimes.

 

In the plastic regime $a<r<c$

(i) We anticipate that ${\sigma }_{rr}<0{\sigma }_{\theta \theta }={\sigma }_{\varphi \varphi }>0$. The yield criterion then gives ${\sigma }_{\theta \theta }-{\sigma }_{rr}=Y$.

(ii) Substituting this result into the equilibrium equation given in Sect 4.2.2 shows that

$\frac{d{\sigma }_{rr}}{dr}+\frac{1}{r}\left(2{\sigma }_{rr}-{\sigma }_{\theta \theta }-{\sigma }_{\varphi \varphi }\right)=0\Rightarrow \frac{d{\sigma }_{rr}}{dr}-2\frac{Y}{r}=0$

(iii) Integrating, and using the boundary condition ${\sigma }_{rr}=-p_{a}r=a$ together with the yield condition (i) gives

 ${\sigma }_{rr}=2Y\log (r/a)-p_a{\sigma }_{\theta \theta }={\sigma }_{\varphi \varphi }=2Y\log (r/a)-p_a+Y$

(iv) Since the pressure is monotonically increasing, the incremental stress-strain relations for the elastic-plastic region given in 4.2.2 can be integrated. The elastic strains follow as

${\epsilon }_{rr}^e=\left({\sigma }_{rr}-2\nu {\sigma }_{\theta \theta }\right)/E{\epsilon }_{\varphi \varphi }^e={\epsilon }_{\theta \theta }^e=\left((1-\nu ){\sigma }_{\theta \theta }-\nu {\sigma }_{rr}\right)/E$

(v) The plastic strains satisfy ${\epsilon }_{rr}^p+2{\epsilon }_{\theta \theta }^p=0$.  Consequently, using the strain partition formula, the results of (iv), and the strain-displacement relation shows that

$\begin{array}{l}{\epsilon }_{rr}+2{\epsilon }_{\theta \theta }={\epsilon }_{rr}^e+2{\epsilon }_{\theta \theta }^e=\frac{(1-2\nu )}{E}\left({\sigma }_{rr}+2{\sigma }_{\theta \theta }\right)\\ \Rightarrow \frac{du}{dr}+\frac{2u}{r}=\frac{1}{r^2}\frac{d}{dr}\left(r^{2}u\right)=\frac{(1-2\nu )}{E}\left(6Y\log (r/a)-3p_a+2Y\right)\end{array}$

(vi) Integrating gives

$u=\frac{\left(1-2\nu \right)}{E}r\left\{2Y\log (r/a)-p_a\right\}+C/r^2$

where C is a constant of integration

(vii) The constant of integration can be found by noting that the radial displacements in the elastic and plastic regimes must be equal at r=c.  Using the expression for the elastic displacement field below and solving for C gives

$C=\frac{3}{2}\frac{\left(1-\nu \right)c^3{b}^3}{E(b^3-c^3)}\left\{p_a-2Y\log (c/a)\right\}$

This result can be simplified by noting that $p_a-2Y\log (c/a)=2Y(1-c^3/b^3)/3$ from the expression for the location of the elastic-plastic boundary given below.

 

 

 

In the elastic regime

The solution can be found directly from the solution to the internally pressurized elastic sphere given in Sect 4.1.4.  From step (iii) in the solution for the plastic regime we see that the radial pressure at r=c is $p_c=-{\sigma }_{rr}=p_a-2Y\log (c/a)$. We can simplify the solution by noting $p_a-2Y\log (c/a)=2Y(1-c^3/b^3)/3$ from the expression for the location of the elastic-plastic boundary.   Substituting into the expressions for stress and displacement shows that

${\sigma }_{rr}=\frac{p_c{c}^3}{\left(b^3-c^3\right)}\left(1-\frac{b^3}{r^3}\right)$           ${\sigma }_{\theta \theta }={\sigma }_{\varphi \varphi }=\frac{p_c{c}^3}{\left(b^3-c^3\right)}\left(1+\frac{b^3}{2r^3}\right)$

$u=\frac{p_c{c}^3}{2E\left(b^3-c^3\right)r^2}\left\{2\left(1-2\nu \right)r^3+\left(1+\nu \right)b^3\right\}{e}_r$

 

 

 

Location of the elastic-plastic boundary

Finally, the elastic-platsic boundary is located by the condition that the stress in the elastic region must just reach yield at r=c (so there is a smooth transition into the plastic region).  The yield condition is ${\sigma }_{\theta \theta }-{\sigma }_{rr}=Y$, so substituting the expressions for stress in the elastic region and simplifying yields

${\sigma }_{\theta \theta }-{\sigma }_{rr}=\frac{3\left(p_a-2Y\log (c/a)\right)b^3}{2\left(b^3-c^3\right)}=Y\iff \frac{p_a}{Y}=2\log (c/a)+\frac{2}{3}(1-c^3/b^3)$

If $p_a$, Y, a and b are specified this equation can be solved (numerically) for c.  For graphing purposes it is preferable to choose c and then calculate the corresponding value of $p_a$