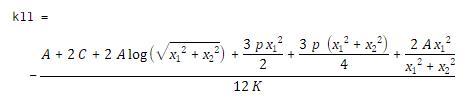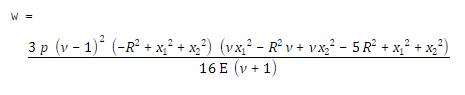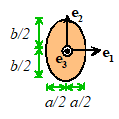Chapter 11
Analyzing
solids with special shapes
Calculating
the full 3D displacement field, along with all 9 stress and strain components
in a solid can be difficult (even with the latest finite element
software). For some solids with special
shapes, the analysis can be simplified by making assumptions about how the
stress and strain vary in the solid.
This can be particularly helpful to analyze structural elements, such as
rods, beams, plates and shells.
In
this chapter we will discuss how to analyze deformation of straight beams and
flat plates, to illustrate the main ideas.
There is a large literature on analysis of structural elements, which is
often taught in a sequence of several courses, and cannot be discussed fully
here. Our main goal is to provide
enough background in the subject so you can set up and interpret finite element
simulations that include some of these structural elements
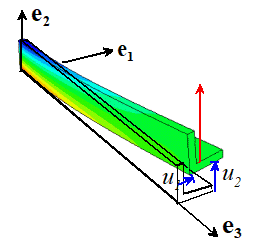 11.1 Analyzing
Deformation and Motion of Straight Beams and Strings
11.1 Analyzing
Deformation and Motion of Straight Beams and Strings
We
start by discussing simplified solid mechanics theories that describe motion of
slender rods and beams. The figure
shows the problem to be solved. To keep
the discussion (reasonably) simple here, we will assume
 The solid is a straight beam, with a uniform
cross-section (in FEA simulations, beams can be curved, and the cross-section
can vary along the length of the beam)
The solid is a straight beam, with a uniform
cross-section (in FEA simulations, beams can be curved, and the cross-section
can vary along the length of the beam)
 We will describe position and motion of the
beam using a local Cartesian coordinate system with parallel to the axis of the beam. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the part.
We will describe position and motion of the
beam using a local Cartesian coordinate system with parallel to the axis of the beam. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the part.
 Deflections are small (FEA simulations can
handle large deformations)
Deflections are small (FEA simulations can
handle large deformations)
 We will neglect twisting of the cross section i.e. in the figure, the cross section does not
rotate about the axis.
(You can include twist in FEA simulations; there are also several
analytical methods for analyzing twisting of beams or rods, depending on the
shape of the cross-section)
We will neglect twisting of the cross section i.e. in the figure, the cross section does not
rotate about the axis.
(You can include twist in FEA simulations; there are also several
analytical methods for analyzing twisting of beams or rods, depending on the
shape of the cross-section)
Characterizing the Geometry of the cross-section
In
most FEA programs you can specify the geometry of the cross-section by simply
entering relevant dimensions for standard cross-sections (circles, rectangles,
I-beams, C and L sections and so on).
The software will compute all relevant integrated quantities
internally.
When
we analyze deformation of straight elastic beams by hand, we start by
introducing a convenient coordinate system: will be an axial unit vector, and are two convenient directions in the plane of
the cross-section (in FEA calculations the cross-sectional geometry is
specified in a local coordinate system with tangent to the beam axis. The orientation of the directions with respect to the global coordinate system
must be specified separately). We then
calculate the following geometrical quantities:
1.
The
cross-sectional area
2.
The position of
the neutral line in the cross section (this is a fiber in the beam that does
not stretch as the beam bends)
3. The components of the area moment of inertia tensor
for the cross-section
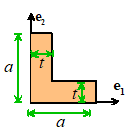
The
integrals are always a pain to evaluate.
It is usually simplest to do them with a symbolic manipulation
program. As an example, here is a
MATLAB live script that calculates the relevant quantities for a symmetric
L-shaped cross-section. To adapt this
to different shapes you usually just need to work out how to handle the limits
in the area integral the integrands don’t change.
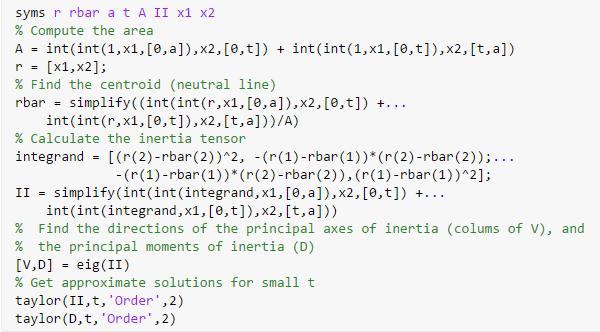
The
solution is
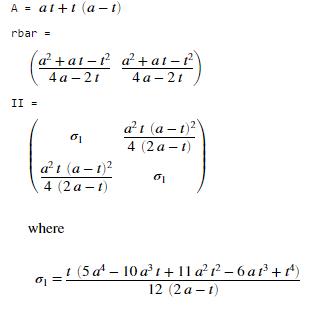
For small t/a we can use the approximation
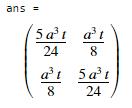
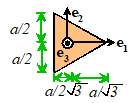
Since
I is a (2D) tensor, we can use all
our secret tensor manipulation superpowers to manipulate it. For example, the principal values and
directions of I are useful (they are
the eigenvalues and eigenvectors of I. The eigenvectors can be visualized as a
special basis in which I is
diagonal; the corresponding eigenvalues are the values of in this basis.
For the L-shaped cross
section Matlab says the principal axes of
inertia (the eig command) are
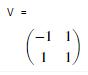
The columns of V are the eigenvectors, but they are not
unit vectors. This tells us that
The
principal moments of area are
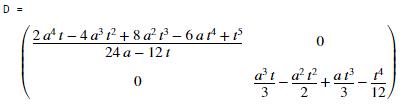
For
small t/a this is
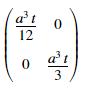
The
top left diagonal is the moment of area about ; the bottom right is the moment of area about
.
The
table below gives area moments of inertia for some simple shapes. You can find more tabulated values online.
|
Areas and area moments of inertia for simple
cross-sections
|
|
|
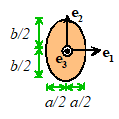
|
|
|
|
|
|
 Approximating
the deformation of a beam
Approximating
the deformation of a beam
The
deformed shape of a straight beam is described by specifying the displacement of each point on the neutral line of the
cross-section, as a function of position along the length of the beam. If the beam twists (not discussed here), it
is also necessary to calculate the angle of rotation of the cross-section about
the axis.
Two additional geometric
variables are used to describe the deformed geometry of a beam. These are:
1. The (small) rotation of the cross-section
The
sign conventions used to describe rotations is confusing the angles represent small rotations, in
radians, about the axes.
The small rotation is a vector, and is related to the displacement by .
(If twist is included there is a third rotation angle that specifies the
rotation of the cross section about the axis).
2. The curvature of the beam
The
curvature is also a vector, and is related to the slope and displacement
vectors by
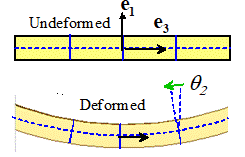
There
are two main flavors of beam theory: the simplest one, called ‘Euler-Bernoulli’
beam theory, assumes that material fibers that are transverse to the neutral
line remain transverse after deformation, as shown in the figure above (the
solid blue lines are normal to the dashed blue line). The axial strain distribution in the beam is
then
The
second version of beam theory (called ‘Timoshenko) beam theory allows material
fibers transverse to the neutral line to rotate. This theory is more complex (because you
need to solve for the rotations of the transverse fibers) and won’t be
discussed here, but it is available in most FEA packages. Roughly, Timoshenko theory should be used
for beams that are shorter than about 10 times their thickness; Euler-Bernoulli
or Timoshenko theory can be used for long, slender beams (and will give the
same predictions).
Describing external loads applied to beams
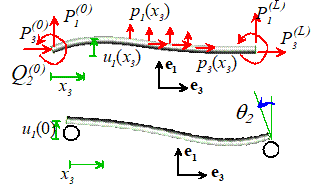 You can load a beam by
You can load a beam by
1.
Applying a distributed
force (load per unit axial length) along the length of the beam.
2.
Either
prescribing the transverse displacement
at the end, or applying forces P(0) P(L) at the ends of the beam (the forces can also be zero at a free
end). The forces are related to the
tractions acting on the ends of the beam by
3.
Either
prescribing the rotation , or applying a moment to the end of the beam (in more general
theories a twist or twisting moment can also be applied parallel to the beam
axis, but we have neglected twisting here to keep things simple). The
components are related to the tractions acting on the end of the rod by
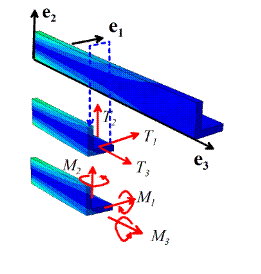 Describing
internal forces in beams
Describing
internal forces in beams
The
forces in a beam are quantified by internal force and moment vectors acting on
each cross-section. To make this
precise, introduce an imaginary cut perpendicular to the axis of the beam, as
shown in the figure. The stresses acting
on an interior face with normal parallel to the direction exert resultant forces T, and bending moments M (if twisting is neglected ,
but all three components have been shown to make it clear that M is a 3D vector).
Beam
theory calculates these resultant forces and moments directly (by solving the
equations of motion or equilibrium in terms of T and M), instead of
solving the 3D equations for the internal stresses. Formally, the theory works by calculating
the axial stress in the beam using the stress-strain relations and the
strain-curvature relations, and then calculating the bending moments using
The
internal forces T in Euler-Bernoulli
beam theory are constraint forces, which act to prevent the beam from
stretching axially, and to keep transverse fibers perpendicular to the neutral
line. They can’t be calculated directly
using the deformation and stress-strain laws, and instead are calculated using
the momentum balance equations in the next section.
Note
that T and M are vectors, and by default ABAQUS will report their components
in the global coordinate system by default.
Moment-Curvature relations for elastic beams
In an elastic beam with Youngs modulus E, the bending moment vector is related
to the curvature vector by
It is easy to derive these:
1. Recall that the axial strain in the beam is
2. The elastic stress-strain law gives
3. The bending moments are .
4. Finally, substitute for the stress and simplify using
the definition of the inertia tensor
Equations of motion for small deflections of straight
beams subjected to significant axial force
Consider
a beam with mass density , cross-sectional area A , which is subjected to a transverse distributed force per unit
length ,
along with relevant forces or constraints at its ends. The loading induces an acceleration vector and curvature vector , along with internal forces and bending moment. . The
equations of motion for the beam are
- Linear momentum balance
- Angular momentum balance
These can also be written
in more compact vector form
At the ends of the beam,
the internal force T and M must satisfy boundary conditions
1. Where forces are prescribed
2. Where moments are prescribed
For
an elastic beam, the transverse internal forces and curvature can all be
eliminated to get two coupled differential equations for the transverse
deflections of the beam
In
terms of displacements, the possible boundary conditions are:
1.
Prescribed displacements
or
Prescribed forces where the two transverse forces are related
to the displacements by
2.
Prescribed
rotations or
Prescribed moments where the moment is related to the
displacement by
Special cases:
 Two limiting cases of these equations are often
used.
Two limiting cases of these equations are often
used.
1.
Stretched string: If the bending resistance is small compared with the axial force ( ) we get the equation of motion for a
stretched string
In this case the equations for motion in the two
transverse directions always decouple. The
boundary conditions at the ends of the string are:
(a)
Either: prescribed
transverse displacement or
prescribed transverse force
(b)
The axial force
must satisfy
Only displacements and forces can be prescribed at the
ends of a string; the moments are always zero
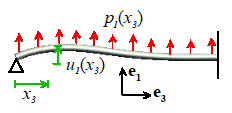
2.
Beam with zero axial force. In many cases
the axial forces in the beam can be neglected.
In this case the equations of motion simplify to
It is often convenient to choose the directions so that . The
equations for the two transverse deflections then decouple.
We
close this section with two remarks:
1.
It is important
to remember that these are approximate equations, and only apply to straight
beams with small transverse deflections and no twist. More general equations do exist, of course.
2.
The linear
momentum balance equations given here are in terms of force components in the
fixed basis.
The same equations can be expressed in terms of components of internal
and moment in a basis which rotates with the beam. These results look slightly
different, but give the same governing equations for the displacement
components.
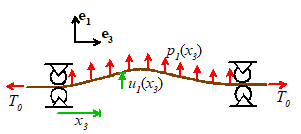
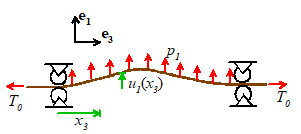 Example 1: The figure shows a flexible string (i.e. a beam with ) subjected to a uniform transverse load p. Calculate the transverse deflection.
Example 1: The figure shows a flexible string (i.e. a beam with ) subjected to a uniform transverse load p. Calculate the transverse deflection.
Start by calculating the
tension in the string. The equation for
axial force is
Since there is no axial
force or acceleration, the tension is constant. The boundary conditions at the end show .
We can now use the equation
for transverse motion (we only need to worry about the vertical component, and
there is no acceleration) which can be simplified to
We don’t even need Matlab
to solve this:
The transverse deflection
is zero at , which shows that . The
solution is therefore
 Example
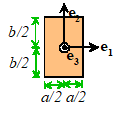
2: The figure shows a cantilever beam with an L-shaped cross-section. Its moment of inertia tensor can be
approximate by
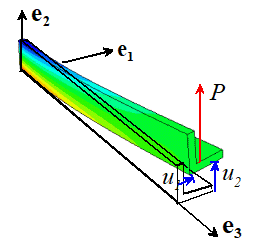
Example
2: The figure shows a cantilever beam with an L-shaped cross-section. Its moment of inertia tensor can be
approximate by
The
beam is prevented from displacing or rotating at and is subjected to a vertical force P at .
Calculate the deflections
For
a beam in static equilibrium, with no axial load, and with no loads applied
along the length of the beam we have that
The boundary conditions are
1. Zero displacement and rotation at
2. Zero moment at
3. Prescribed force at
It is not hard to solve
these by hand the general solution for are just polynomials with unknown coefficients
but it’s terribly boring to do the
algebra. A MATLAB ‘Live script’ is much
faster
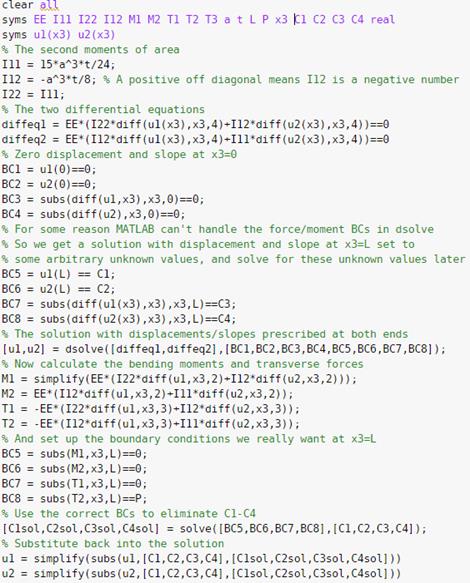
The MATLAB solution is
shown.
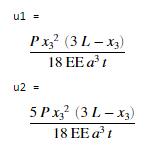
Notice
that a vertical load causes a horizontal, as well as vertical
displacement. This is because the
cross-section is unsymmetric if the beam deflected only vertically, the vertical
side of the L would be in compression near its top, which would exert a
non-zero moment on the cross-section about the axis.
Analyzing beams in ABAQUS
We end this section by
discussing briefly how to set up an ABAQUS simulation that contains beams.
Part module:
1.
To create a beam
in the ‘Part’ module, use Part->Create New and then select a 3D deformable
object with a ‘Wire’ base feature. Then
draw a line that will define the shape of the beam.
2.
If you create a
curved beam, you might find it helpful to create one or more local coordinate
systems with axes oriented tangent and perpendicular to the beam. It is usually easiest to make the x direction
of the new system tangent to the beam. You can do this by selecting Tools > Datum…
and clicking the CSYS box. There are a
few different options for creating local coordinate systems. If you select the ‘3 points’ method, ABAQUS
will ask you to select an origin for your coordinate system, and then will ask
you to put in coordinates (in the global coordinate system) for an origin, a
point that lies on the x axis of the new system, and a second point in the new
system that should lie in the current global x-y plane (this is confusing just try it a few times to figure out what it
does).
Property module
In
the ‘Property’ module you will need to define the properties of the beam cross
section.
1.
Define a set of
material properties in the usual way (Material, Create New, etc).
2.
Then create a
profile (Profile, Create new); select the shape and then enter the relevant
geometric variables.
3.
Next, create a
beam section by going to Section > Create… and select Beam. You can then select the profile and material
you want to use to define your beam section.
The ‘Section integration’ will calculate the moment of inertia tensor
for an elastic beam, or for other materials will integrate the stresses on the
fly to calculate moments and shear forces.
Selecting ‘During analysis’ is the safest option.
4.
Once the section
is created, you can assign it to the relevant section of the beam (Assign >
Section).
5.
Finally you need
to specify the orientation of the cross section of the beam. Select Assign > Beam section orientation,
then enter the information requested.
The default option makes the ‘1’ direction of the profile parallel to
the z global coordinate direction.
Assembly module: There is nothing special about the assembly modules
for beams.
Interaction module
 You often need
to analyze a structure consisting of a number of separate beams connected
together. You will need to create each
beam as a separate part, and then specify how they are connected in the
interaction module. To do this,
You often need
to analyze a structure consisting of a number of separate beams connected
together. You will need to create each
beam as a separate part, and then specify how they are connected in the
interaction module. To do this,
1.
Select
Constraint> Create
2.
Select ‘Node
Region’ from the menu and then select the end of one of the two beams you want
to connect. Accept the choice (if it is
the correct one!) then select the end of the second beam. If you need to, you can hide members in the
assembly by going to the Assembly tab in the model database tree, expand the
‘Instances’ branch, and then right click the part you want to hide. Annoyingly if you do this at the wrong time
it will end the constraint creation.
Usually if you select the first beam with all the parts shown (this will
select the beam that was added to the assembly last), then wait until the ‘node
region’ button appears for the second beam, you can operate the ‘hide’ and
‘show’ buttons without leaving the constraint definition menu..
3.
In the constraint
menu you can choose whether you want to connect the beams with a welded joint
(check the Tie rotational DOF box) or a pin joint (uncheck the tie rotational
DOF box).
Step module
 You can define a ‘step’ in the usual way. To get the simple small deflection version of
beam theory defined in these notes, make sure the NLGEOM option is not
selected. If you select NLGEOM, ABAQUS
will do a large displacement/rotation calculation. These can be highly nonlinear and if you run
a simulation without thinking through the proper magnitudes for loads and
section properties, the analysis is likely to fail.
You can define a ‘step’ in the usual way. To get the simple small deflection version of
beam theory defined in these notes, make sure the NLGEOM option is not
selected. If you select NLGEOM, ABAQUS
will do a large displacement/rotation calculation. These can be highly nonlinear and if you run
a simulation without thinking through the proper magnitudes for loads and
section properties, the analysis is likely to fail.
If
you want ABAQUS to display the internal forces and moments in your beam, you
will need to request that they be stored during the analysis. To do this, select Output > Field Output
Requests > Create and make sure the ‘Section Forces and Moments’ box is
checked in the ‘Forces/Reactions’ list
Load Module
For the most part, you can
define boundary conditions and forces in the Load module in the same way that
you would for a 3D solid part. The
differences are:
1. In beam analysis, the nodes have rotational as well as
translational degrees of freedom (because you need to be able to specify
slopes/moments acting on the beam). The
rotational degrees of freedom are shown as UR1, UR2, UR3 in the ‘Boundary
condition’ definition window. For small
rotations, the three components of the rotation vector defined in these notes (in radians) you can select what coordinate system you want
to use to define its components. Large
rotation don’t behave like vectors - in
this case ABAQUS uses UR1, UR2, UR3 to be the components in the axis-angle
description of the rotation tensor. The
direction is the axis of rotation, and the magnitude is the rotation angle
about the axis.
2. You can apply moments to beams.
Mesh Module
You will need to mesh your
beams to do this, ‘seed’ them with nodes in the
usual way, then mesh the part (or instance, whichever ABAQUS lets you do). The default element types usually work; but
as always with mesh design it is sensible to run the analysis with several
different element types and meshes to check mesh sensitivity. If the choice of element type or mesh makes
a difference, you will need to decide which element type and mesh gives the
most accurate solution.
Job Module set up jobs in the usual way.
Visualization Module
You can display
displacements in the usual way.
ABAQUS will also display
section forces and moments, and will also plot stresses in your beam. Interpreting what is shown is tricky.
1.
To display internal
forces in the beam (the vector T
defined in these notes) select Result > Field Output and the select  from the menu.
The sign convention is confusing: SF1 is the axial force in the beam,
SF2 and SF3 are the forces in the local (1) and (2) coordinate system for the
beam (you defined these in the Property module).
from the menu.
The sign convention is confusing: SF1 is the axial force in the beam,
SF2 and SF3 are the forces in the local (1) and (2) coordinate system for the
beam (you defined these in the Property module).
2.
To display
internal moments select  . The variables SM1, SM2 are the bending
moments about the local ‘1’ and ‘2’ axes, and SM3 is the twisting moment.
. The variables SM1, SM2 are the bending
moments about the local ‘1’ and ‘2’ axes, and SM3 is the twisting moment.
3.
ABAQUS also
allows you to display stresses in the beam.
Since the stress varies with position in the cross-section you need to
select which point in the cross-section to use: you can select the points using
the Section Points… button in the Field Output selection window.
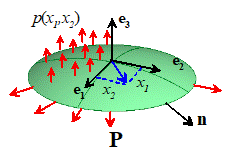
11.2 Analyzing Deformation and Motion of
Flat Plates
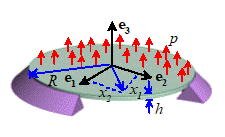 We next consider simplified solid mechanics theories
that describe motion of flat plates.
The figure shows the problem to be solved. To keep the discussion (reasonably) simple
here, we will assume
We next consider simplified solid mechanics theories
that describe motion of flat plates.
The figure shows the problem to be solved. To keep the discussion (reasonably) simple
here, we will assume
 The solid is a flat plate, with a uniform
thickness h (in FEA simulations,
plates can be curved (then they are called shells), and the thickness can vary)
The solid is a flat plate, with a uniform
thickness h (in FEA simulations,
plates can be curved (then they are called shells), and the thickness can vary)
 We will describe position and motion of the
beam using a local Cartesian coordinate system with perpendicular to the plate. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the
part.
We will describe position and motion of the
beam using a local Cartesian coordinate system with perpendicular to the plate. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the
part.
 Deflections are small (FEA simulations can
handle large deformations)
Deflections are small (FEA simulations can
handle large deformations)
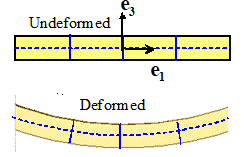 Approximating
the deformation of a plate
Approximating
the deformation of a plate
The
deformed shape of a flat plate is described by specifying the displacement of each point on the centerline of the a
function of position in the plane.
Two additional geometric
variables are used to describe the deformed geometry of a beam. These are:
3. The (small) rotation of the cross-section
The
angles represent small rotations, in radians, about the axes.
The small rotation is a vector, and is related to the displacement by .
4. The curvature of the plate
The
curvature is a (2D) tensor, and is related to the rotation vector by
There
are two main flavors of plate: the simplest one, called ‘Kirchhoff’ theory,
assumes that material fibers that are transverse to the plane of the plate
remain transverse after deformation, as shown in the figure above (the solid
blue lines are normal to the dashed blue line).
The strain distribution in the plate is then
The
second version of beam theory (called ‘Reissner-Mindlin’ beam theory) allows
material fibers transverse to the neutral line to rotate. This theory is more complex (because you
need to solve for the rotations of the transverse fibers) and won’t be
discussed here, but it is available in most FEA packages. Roughly, Kirchoff theory should be used for
plates that have width less than than about 10 times their thickness; Kirchoff
or Reissner theory can be used for wide, thin plates (and will give the same
predictions).
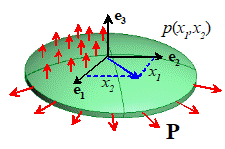 Describing
external loads applied to plates
Describing
external loads applied to plates
To keep things simple, we
consider two types of external loading:
1.
A transverse
pressure acting normal to the surface of the plate, and
2.
A uniform force
per unit length P acting normal to
the perimeter of the plate.
In
more general treatments, it is possible to apply forces acting transverse to
the edge of the plate, as well as moments that cause the edge of the plate to
rotate. It is also possible to make P vary around the perimeter.
Internal forces in plates
The
forces in a plate are quantified by internal force and moment tensors acting on
each cross-section. To make this
precise, cut a square element from the plate with planes normal to the
coordinate axes as shown in the figure. A
set of resultant forces and moments act on the exposed faces:
 The
moments are defined by
The
moments are defined by
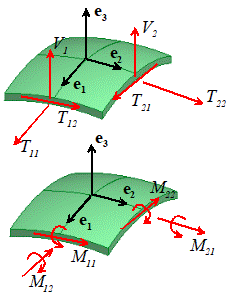 The physical significance of the components is illustrated in the figure: characterizes the moment per unit length
acting on planes inside the shell that are normal to the direction, while characterizes the moment per unit length
acting on planes that are normal to . Note that represents a moment about the axis, while is a moment acting about the axis. This can be expressed mathematically as where the repeated indices are summed over 1 and 2, but this expression
is only helpful if you are really good at visualizing dyadic and cross
products.
The physical significance of the components is illustrated in the figure: characterizes the moment per unit length
acting on planes inside the shell that are normal to the direction, while characterizes the moment per unit length
acting on planes that are normal to . Note that represents a moment about the axis, while is a moment acting about the axis. This can be expressed mathematically as where the repeated indices are summed over 1 and 2, but this expression
is only helpful if you are really good at visualizing dyadic and cross
products.
 The
in-plane forces are defined by
The
in-plane forces are defined by
They
represent resultant forces exerted by stresses on the internal planes: are the components of force acting on the
plane perpendicular to the direction, while are those acting on the plane perpendicular to
the direction.
In general, all three components of resultant force can be
different. But here, we consider only
the simple case of uniform transverse loading applied to the perimeter of the
plate. Under these conditions the
internal forces satisfy , where is the magnitude of the transverse force.
 The
transverse forces represent forces acting in the direction on planes perpendicular to the and direction, respectively.
The
transverse forces represent forces acting in the direction on planes perpendicular to the and direction, respectively.
Moment-Curvature and force-strain relations for
elastic plates
The internal forces are
related to the curvatures and strains by
It is easy to derive these:
the plate is in a state of plane stress: the stresses are therefore related to
the strains by
Substituting for the
strains in terms of displacements and curvatures, and evaluating the integrals,
gives the results stated.
The
transverse forces cannot be determined directly from the
curvatures or motion of the plate. They
represent constraint forces, which act to ensure that lines perpendicular to
the mid-plane of the plate remain perpendicular after the plate deforms. They can be calculated from the linear and
angular momentum balance equations given in the next section.
Equations of motion for small
deflections of flat plates subjected to significant in-plane force
 Consider a plate with mass density , thickness h , which is subjected to a transverse distributed force per unit
area ,
along with relevant forces or constraints at its edges. The loading induces a transverse displacement
acceleration vector and curvature tensor components , along with internal forces and bending moments . The
equations of motion for the plate are
Consider a plate with mass density , thickness h , which is subjected to a transverse distributed force per unit
area ,
along with relevant forces or constraints at its edges. The loading induces a transverse displacement
acceleration vector and curvature tensor components , along with internal forces and bending moments . The
equations of motion for the plate are
1. Linear momentum: (transverse motion)
2. Angular momentum
These equations can be
combined to eliminate V
This result can also be
expressed in terms of displacement as
The
equation can also be written in polar coordinates as
 Edge boundary conditions. The edge of
the plate is characterized by a curve C
that lies in the mid-plane of the shell,
encircling in a counterclockwise sense. We let denote arc-length measured around C from some convenient origin, and use and denote unit vectors tangent and normal to C.
Elementary plate theory offers the following choices of boundary
condition for each point on C:
Edge boundary conditions. The edge of
the plate is characterized by a curve C
that lies in the mid-plane of the shell,
encircling in a counterclockwise sense. We let denote arc-length measured around C from some convenient origin, and use and denote unit vectors tangent and normal to C.
Elementary plate theory offers the following choices of boundary
condition for each point on C:
- Part of the boundary
of the plate may be clamped, i.e.
rotations and displacement of the boundary are completely prevented. The
transverse displacement must then satisfy
on .
- Part of the boundary may be simply supported, i.e. the boundary of the plate is prevented
from moving, but is permitted to rotate freely about the tangent vector . In this case the transverse displacement
and internal moment must satisfy
- Part of the boundary may be free, i.e. the boundary is free to both translate and
rotate. In this case the transverse
shear force and internal moment must satisfy
Special Cases
There
are two special cases of these equations
1. Stretched
Membrane If the bending resistance is
small compared with the in plane tension we get the equation of motion for a biaxially stretched
membrane
or
in polar coordinates
The
possible boundary conditions for a biaxially stretched membrane are:
(a)
Either prescribed
transverse displacements at the edge of the membrane or
Prescribed
transverse force at the membrane edge
(b)
The membrane
tension is prescribed at the perimeter.
2.
Plate with no in-plane external loading In the limit the in-plane tension can be neglected. In this limit we get the simplified plate
bending equations
The equation can also be written in polar coordinates
as
The
boundary conditions are identical to those for a general plate.
Examples
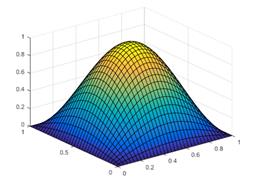 Square
membrane under sinusoidal pressure A
square membrane with dimensions axa is
stretched by edge tension and prevented from displacing transverse to
its own plane at its edges. It is
subjected to a pressure
Square
membrane under sinusoidal pressure A
square membrane with dimensions axa is
stretched by edge tension and prevented from displacing transverse to
its own plane at its edges. It is
subjected to a pressure
Calculate its deflection.
We need to solve
with boundary condition on and
This equation can be solved
by just guessing the solution and substituting into the governing
equation. Assume that . This satisfies the boundary condition. We can find C from the governing equation
The solution is therefore
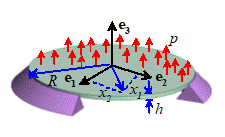 Thin
circular plate bent by pressure applied to one face
Thin
circular plate bent by pressure applied to one face
A
thin circular plate, with radius R
and thickness h is made from a linear
elastic solid with Young’s modulus and Poisson’s ratio ,
as shown in the figure. It is subjected
to a pressure acting perpendicular to the plate, and is
simply supported at its edge. Show that
the deflection of the plate is
The
solution should depend only on r (and
not ) so we the differential equation for the
deflection is
It
is tempting to solve this with MATLAB, but interestingly MATLAB returns an
incorrect solution to this particular ODE at the time of writing these notes
(July 2018). So we have to do it by hand
instead. Expand out the derivatives and
rearrange to get
We
can now just integrate
The
four constants must be determined from the boundary conditions. Note that:
- Note that log(r)
is infinite (and negative) at r=0. But the displacement can’t be
infinite! This means B=0 .
- Now let’s find the curvature of the plate. We can safely use MATLAB to do this. Recall that
For example here’s the calculation of

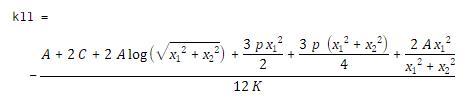
Notice that there’s a term in the solution. Since the curvature can’t be infinite, we
see that A=0.
- The last two boundary conditions are zero
displacement and zero moment about the circumference
of the plate at r=R,
where and are components of a unit vector
perpendicular to the edge of the plate.
This gives two equations for the remaining unknown constants C and D. MATLAB can solve
the equations:

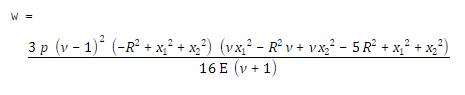
This clearly reduces to the required answer. Note that the MATLAB script will also tell
you the internal moments in the plate, if you care…
 11.1 Analyzing
Deformation and Motion of Straight Beams and Strings
11.1 Analyzing
Deformation and Motion of Straight Beams and Strings![]() The solid is a straight beam, with a uniform
cross-section (in FEA simulations, beams can be curved, and the cross-section
can vary along the length of the beam)
The solid is a straight beam, with a uniform
cross-section (in FEA simulations, beams can be curved, and the cross-section
can vary along the length of the beam)![]() We will describe position and motion of the
beam using a local Cartesian coordinate system with parallel to the axis of the beam. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the part.
We will describe position and motion of the
beam using a local Cartesian coordinate system with parallel to the axis of the beam. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the part. ![]() Deflections are small (FEA simulations can
handle large deformations)
Deflections are small (FEA simulations can
handle large deformations)![]() We will neglect twisting of the cross section i.e. in the figure, the cross section does not
rotate about the axis.
(You can include twist in FEA simulations; there are also several
analytical methods for analyzing twisting of beams or rods, depending on the
shape of the cross-section)
We will neglect twisting of the cross section i.e. in the figure, the cross section does not
rotate about the axis.
(You can include twist in FEA simulations; there are also several
analytical methods for analyzing twisting of beams or rods, depending on the
shape of the cross-section)

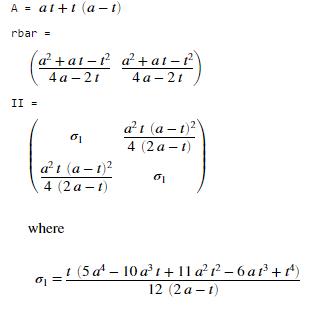
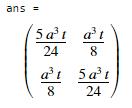
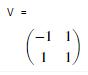
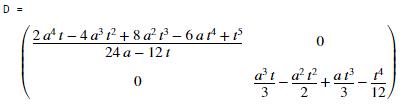
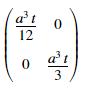
 Approximating
the deformation of a beam
Approximating
the deformation of a beam You can load a beam by
You can load a beam by Describing
internal forces in beams
Describing
internal forces in beams Two limiting cases of these equations are often
used.
Two limiting cases of these equations are often
used. 
 Example 1: The figure shows a flexible string (i.e. a beam with ) subjected to a uniform transverse load p. Calculate the transverse deflection.
Example 1: The figure shows a flexible string (i.e. a beam with ) subjected to a uniform transverse load p. Calculate the transverse deflection. Example
2: The figure shows a cantilever beam with an L-shaped cross-section. Its moment of inertia tensor can be
approximate by
Example
2: The figure shows a cantilever beam with an L-shaped cross-section. Its moment of inertia tensor can be
approximate by
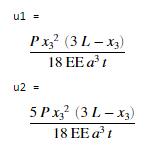
 You often need
to analyze a structure consisting of a number of separate beams connected
together. You will need to create each
beam as a separate part, and then specify how they are connected in the
interaction module. To do this,
You often need
to analyze a structure consisting of a number of separate beams connected
together. You will need to create each
beam as a separate part, and then specify how they are connected in the
interaction module. To do this,  You can define a ‘step’ in the usual way. To get the simple small deflection version of
beam theory defined in these notes, make sure the NLGEOM option is not
selected. If you select NLGEOM, ABAQUS
will do a large displacement/rotation calculation. These can be highly nonlinear and if you run
a simulation without thinking through the proper magnitudes for loads and
section properties, the analysis is likely to fail.
You can define a ‘step’ in the usual way. To get the simple small deflection version of
beam theory defined in these notes, make sure the NLGEOM option is not
selected. If you select NLGEOM, ABAQUS
will do a large displacement/rotation calculation. These can be highly nonlinear and if you run
a simulation without thinking through the proper magnitudes for loads and
section properties, the analysis is likely to fail.![]() from the menu.
The sign convention is confusing: SF1 is the axial force in the beam,
SF2 and SF3 are the forces in the local (1) and (2) coordinate system for the
beam (you defined these in the Property module).
from the menu.
The sign convention is confusing: SF1 is the axial force in the beam,
SF2 and SF3 are the forces in the local (1) and (2) coordinate system for the
beam (you defined these in the Property module). ![]() . The variables SM1, SM2 are the bending
moments about the local ‘1’ and ‘2’ axes, and SM3 is the twisting moment.
. The variables SM1, SM2 are the bending
moments about the local ‘1’ and ‘2’ axes, and SM3 is the twisting moment. We next consider simplified solid mechanics theories
that describe motion of flat plates.
The figure shows the problem to be solved. To keep the discussion (reasonably) simple
here, we will assume
We next consider simplified solid mechanics theories
that describe motion of flat plates.
The figure shows the problem to be solved. To keep the discussion (reasonably) simple
here, we will assume![]() The solid is a flat plate, with a uniform
thickness h (in FEA simulations,
plates can be curved (then they are called shells), and the thickness can vary)
The solid is a flat plate, with a uniform
thickness h (in FEA simulations,
plates can be curved (then they are called shells), and the thickness can vary)![]() We will describe position and motion of the
beam using a local Cartesian coordinate system with perpendicular to the plate. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the
part.
We will describe position and motion of the
beam using a local Cartesian coordinate system with perpendicular to the plate. In an ABAQUS simulation you may want to run
an analysis with the beam pointing along some strange direction in space in this case it can be helpful to create a
local coordinate system with the orientation shown when you create the
part. ![]() Deflections are small (FEA simulations can
handle large deformations)
Deflections are small (FEA simulations can
handle large deformations) Approximating
the deformation of a plate
Approximating
the deformation of a plate Describing
external loads applied to plates
Describing
external loads applied to plates![]() The
moments are defined by
The
moments are defined by The physical significance of the components is illustrated in the figure: characterizes the moment per unit length
acting on planes inside the shell that are normal to the direction, while characterizes the moment per unit length
acting on planes that are normal to . Note that represents a moment about the axis, while is a moment acting about the axis. This can be expressed mathematically as where the repeated indices are summed over 1 and 2, but this expression
is only helpful if you are really good at visualizing dyadic and cross
products.
The physical significance of the components is illustrated in the figure: characterizes the moment per unit length
acting on planes inside the shell that are normal to the direction, while characterizes the moment per unit length
acting on planes that are normal to . Note that represents a moment about the axis, while is a moment acting about the axis. This can be expressed mathematically as where the repeated indices are summed over 1 and 2, but this expression
is only helpful if you are really good at visualizing dyadic and cross
products.![]() The
in-plane forces are defined by
The
in-plane forces are defined by![]() The
transverse forces represent forces acting in the direction on planes perpendicular to the and direction, respectively.
The
transverse forces represent forces acting in the direction on planes perpendicular to the and direction, respectively.  Consider a plate with mass density , thickness h , which is subjected to a transverse distributed force per unit
area ,
along with relevant forces or constraints at its edges. The loading induces a transverse displacement
acceleration vector and curvature tensor components , along with internal forces and bending moments . The
equations of motion for the plate are
Consider a plate with mass density , thickness h , which is subjected to a transverse distributed force per unit
area ,
along with relevant forces or constraints at its edges. The loading induces a transverse displacement
acceleration vector and curvature tensor components , along with internal forces and bending moments . The
equations of motion for the plate are Edge boundary conditions. The edge of
the plate is characterized by a curve C
that lies in the mid-plane of the shell,
encircling in a counterclockwise sense. We let denote arc-length measured around C from some convenient origin, and use and denote unit vectors tangent and normal to C.
Elementary plate theory offers the following choices of boundary
condition for each point on C:
Edge boundary conditions. The edge of
the plate is characterized by a curve C
that lies in the mid-plane of the shell,
encircling in a counterclockwise sense. We let denote arc-length measured around C from some convenient origin, and use and denote unit vectors tangent and normal to C.
Elementary plate theory offers the following choices of boundary
condition for each point on C:
 Square
membrane under sinusoidal pressure A
square membrane with dimensions axa is
stretched by edge tension and prevented from displacing transverse to
its own plane at its edges. It is
subjected to a pressure
Square
membrane under sinusoidal pressure A
square membrane with dimensions axa is
stretched by edge tension and prevented from displacing transverse to
its own plane at its edges. It is
subjected to a pressure Thin
circular plate bent by pressure applied to one face
Thin
circular plate bent by pressure applied to one face