6. Constitutive Laws

 

The equations listed in the preceding sections apply to any solid or fluid that deforms under the action of external forces.   They do not, by themselves, have a unique solution, however, because the deformations are not related in any way to internal forces.

 

The governing equations are completed by constitutive laws that provide the missing connection.  Unlike deformation measures; kinetics; and conservation laws, a constitutive law cannot be calculated or predicted from first principles, except for a few very special cases such as small deformations of crystalline materials, where elastic properties can be estimated using ab-initio techniques that approximate quantum mechanical level atomic scale interactions in some way.

 

6.1 Basic assumptions $–$ local homogeneity of internal forces and deformation; the principle of local action

 

Before discussing specific constitutive models, it is helpful to review the basic assumptions that we take for granted in developing stress-strain laws.  They are listed below.

 A very small sample that is extracted from the solid has uniform properties;

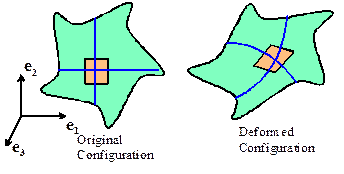
 When the solid is deformed, initially straight lines in the solid are deformed into smooth curves (with continuous slope);

 This means that very short line segments (much shorter than the radius of curvature of the curves) are just stretched and rotated by the deformation.   Consequently, the deformation of a sufficiently small volume element can be characterized by the deformation gradient;

 The stress at a point in the solid depends only on the change in shape of a vanishingly small volume element surrounding the point.  It must therefore be a function of the deformation gradient or a strain measure that is derived from it.

If we accept the preceding assumptions, it means that we can measure the relationship between stress and strain by doing an experiment that induces a uniform strain in a suitable sample of the material.  According to our assumptions, the stress should also be uniform, and can be calculated from the forces acting on the specimen.

 

These are clearly approximations.  Materials are not really uniform at small scales, whether you choose to look at the atomic scale, or the microstructural scale.  However, these features are usually much smaller than the size of the solid part or component, and the material can be regarded as statistically uniform, in the sense that if you cut two specimens with similar size out of the material they will behave in the same way.  A continuum model then describes the average stress and deformation in a region of the material that is larger than microstructural features, but small compared with the dimensions of the part.

 

 

 

6.2 Restrictions on constitutive equations

 

You may be called upon to develop a stress-strain law for a new material at some point of your career.  If so, it is essential to make sure that the stress-strain law satisfies two conditions:

(i) It must obey the laws of thermodynamics.

(ii) It must satisfy the condition of objectivity, or material frame indifference. 

In addition, it is a good idea to ensure that the material satisfies the Drucker stability criterion discussed in more detail below.  Of course, your proposed law must conform to experimental measurements, and if possible should be based on some understanding of the physical processes that govern the response of the solid.   But only the first two conditions apply to all solids.  

 

Thermodynamic restrictions: Constitutive laws usually start by expressing the specific internal or free energy, specific entropy, and heat flux of a material in terms of the temperature, parameters characterizing shape changes, and any internal state variables (such as yield stress) that characterize the material state.  These have the general form

 

$\begin{array}{l}\text{Internal energy: }\epsilon (\theta ,\text{deformation measures,state variables)}\\ \text{Entropy: }s(\theta ,\text{deformation measures,state variables)}\\ \text{Free energy: }\psi (\theta ,\text{deformation measures,state variables) = }\epsilon -\theta s\\ \text{Heat flux response function: }q(\theta ,\text{deformation measures,state variables)}\\ \text{Stress Response Function: }\sigma (\theta ,\text{deformation measures,state variables)}\\ \text{Evolution equations for state variables (these may be functions of temperature, kinematics, and state vars)}\end{array}$

 

For a solid with mass density (in the deformed configuration) $\rho$ experiencing a stretch rate $D_{ij}$ and Cauchy stress ${\sigma }_{ij}$, the first and second laws of thermodynamics then require that

$\rho {\frac{\partial \epsilon }{\partial t}|}_{x=const}={\sigma }_{ij}{D}_{ij}-\frac{\partial q_i}{\partial y_i}+q$

${\sigma }_{ij}{D}_{ij}-\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}-\rho \left(\frac{\partial \psi }{\partial t}+s\frac{\partial \theta }{\partial t}\right)\ge 0$

for all possible processes.

 

In practice, only the second law leads to any restrictions on the constitutive equations.  We assume that the first law can always be satisfied by some appropriate heat flux q.

 

We will see how to use the second law in devising structures for constitutive equations through specific examples in the next few sections.  In practice, a simplified version of the second law is used nearly always used, however, and we summarize this form briefly here.

 

For the majority of problems in solid and fluid mechanics, we do not attempt to model deformation and heat conduction simultaneously (there are exceptions of course, such as high strain rate deformation; thermoelasticity, and so on).   In practice, we can often assume that the solid is in equilibrium with a surrounding heat bath with constant temperature, and heat flow through a solid is sufficiently rapid to ensure that the temperature remains approximately uniform.  Under these conditions the second law reduces to

${\sigma }_{ij}{D}_{ij}-\rho \frac{\partial \psi }{\partial t}\ge 0$

Physically, this states that the rate of work done by stresses must always equal or exceed the rate of change of free energy of the solid. 

 

Frame indifference:  The principle of frame indifference (which is still the subject of some debate) states that constitutive equations must be invariant to a change of observer (all observers, regardless of their reference frame, must describe the same physical process).   The transformation of various field quantities under changes of observer was discussed in the preceding section.   To reiterate, spatial coordinates map as

$y^{*}=y_0^{*}(t)+Q(t)(y-y_0)$

under a change of observer.   In a constitutive model, observers in the two frames will  use some temperature or deformation measures that we will denote by a vague symbol $\Gamma ,{\Gamma }^{*}$ (they could be scalar, vector, or tensor valued variables).  These measures are always related by a appropriate transformation relations under a change of observer $–$ for example, deformation gradients, Lagrange strains, and the Left stretch tensor transform according to $F_{ij}^{*}=Q_{ik}{F}_{kj}{E}_{ij}^{*}=E_{ij}{B}_{ij}^{*}=Q_{ik}{B}_{kl}{Q}_{jl}$.   The constitutive model will predict some physical quantity of interest in terms of these variables.  We will denote the predicted quantity in the two frames by a similar vague variable $\Phi ,{\Phi }^{*}$, which could be a scalar, vector or tensor valued quantity.   For example, the constitutive model could predict the free energy $\psi$, the heat flux vector $q_i$ or Cauchy or Material stress ${\sigma }_{ij},{\Sigma }_{ij}$.   Again, we know how these physical quantities transform under a change of observer $–$$\psi ={\psi }^{*}{q}_i^{*}=Q_{ik}{q}_i{\sigma }_{ij}^{*}=Q_{ik}{\sigma }_{kl}{Q}_{jl}{\Sigma }_{ij}^{*}={\Sigma }_{ij}$.    The functions relating these  variables to the kinematic variables must behave correctly under a change of observer $–$ in general

$\Phi =f(\Gamma )\iff {\Phi }^{*}=f({\Gamma }^{*})$

As a specific example, a constitutive relation specifying the Cauchy stress in terms of deformation gradient would have to transform according to

$\begin{array}{l}{\sigma }_{ij}^{}=f_{ij}(F_{ij}^{})\iff {\sigma }_{ij}^{*}=f_{ij}(F_{ij}^{*})\\ \iff Q_{ik}{\sigma }_{kl}{Q}_{jl}=f_{ij}(Q_{ik}{F}_{kj}^{})\iff Q_{ik}{f}_{kl}(F_{ij})Q_{jl}=f_{ij}(Q_{ik}{F}_{kj}^{})\end{array}$

This restricts the possible form of the function $f_{ij}$.   You can use a similar process to crank out restrictions for any kind of constitutive relation.  

 

There is still some debate as to whether frame indifference should apply under a transformation between frames in relative rotation.   Usually, it is assumed that constitutive equations must hold even in a non-inertial frame.   But some fluid mechanics models of turbulent flow, for example, attempt to describe macroscopic behavior of a volume element of fluid that has internal angular momentum.   Constitutive laws of this kind can only hold in an inertial frame, and so invariance need only apply during a transformation from one inertial frame to another.   These have the form

$y^{*}=y_0^{*}+Q(y-y_0)$

(the time dependence is gone).   

 

 

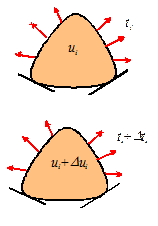
Drucker Stability:  For most practical applications, the constitutive equation must satisfy a condition known as the Drucker stability criterion, which can be expressed as follows.  Consider a deformable solid, subjected to boundary tractions $t_i$, which induce some displacement field $u_i$.  Suppose that the tractions are increased to $t_i+\Delta t_i$, resulting in an additional displacement $\Delta u_i$. The material is said to be stable in the sense of Drucker if the work done by the tractions $\Delta t_i$ through the displacements $\Delta u_i$ is positive or zero for all $\Delta t_i$:

$\Delta W={\displaystyle \int \left\{{\displaystyle \underset{A}{\int }\Delta t_i\frac{d\Delta u_i}{dt}}\right\}}dt\ge 0$

You can show that this condition is satisfied as long as the stress-strain relation obeys

$\Delta {\tau }_{ij}\Delta {\epsilon }_{ij}\ge 0$

where $\Delta {\tau }_{ij}$ is the change in Kirchhoff stress, and $\Delta {\epsilon }_{ij}=(\partial \Delta u_i/\partial x_j+\partial \Delta u_j/\partial x_i)$ is an increment in strain resulting from an infinitesimal change in displacement $\Delta u_i$.

 

This is not a thermodynamic law (the work done by the change in tractions is not a physically meaningful quantity), and there is nothing to say that real materials have to satisfy Drucker stability. In fact, many materials show clear signs that they are not stable in the sense of Drucker.   However, if you try to solve a boundary value problem for a material that violates the Drucker stability criterion, you are likely to run into trouble.  The problem will probably not have a unique solution, and in addition you are likely to find that smooth curves on the undeformed solid develop kinks (and may not even be continuous) after the solid is deformed.  This kind of deformation violates one of the fundamental assumptions underlying continuum constitutive equations. 

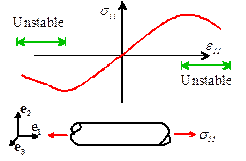
A simple example of a stress-strain curve for material that is not stable in the sense of Drucker is shown in the picture.  The stability criterion is violated wherever the stress decreases with strain in tension, or increases with strain in compression. For the former we see that $\Delta {\sigma }_{11}<0$, while $\Delta {\epsilon }_{11}>0$; for the latter $\Delta {\sigma }_{11}>0$, while $\Delta {\epsilon }_{11}<0$.