4. Kinetics
Our
next objective is to outline the mathematical formulas that describe internal
and external forces acting on a solid.
Just as there are many different strain measures, there are several
different definitions of internal force.
We shall see that internal forces can be described as a second order
tensor, which must be symmetric. Thus,
internal forces can always be quantified by a set of six numbers, and the
various different definitions are all equivalent.
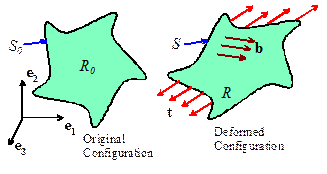 4.1 Surface traction and internal body force
4.1 Surface traction and internal body force
Forces
can be applied to a solid body in two ways.
(i) A force can be applied to its
boundary: examples include fluid pressure, wind loading, or forces arising from
contact with another solid.
(ii) The solid can be subjected to body forces, which act on the interior
of the solid. Examples include
gravitational loading, or electromagnetic forces.
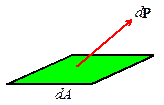
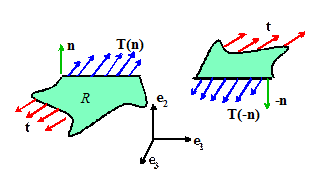
 The surface
traction vector t at a point
on the surface represents the force acting on the surface per unit area of the
deformed solid.
The surface
traction vector t at a point
on the surface represents the force acting on the surface per unit area of the
deformed solid.
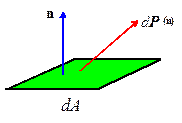
Formally,
let dA be an element of area on a
surface. Suppose that dA is subjected to a force . Then
The
resultant force acting on any portion S of
the surface of the deformed solid is
Surface traction, like `true stress,’ should be
thought of as acting on the deformed solid.
 Normal and shear tractions
Normal and shear tractions
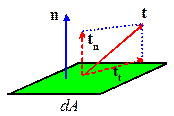
The traction vector is often resolved into components acting
normal and tangential to a surface, as shown in the picture.
The normal component is referred to as the normal traction, and the tangential
component is known as the shear traction.
Formally, let n denote a unit vector normal to the surface. Then
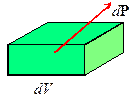
 The body
force vector denotes the external force acting on the interior of a
solid, per unit mass.
The body
force vector denotes the external force acting on the interior of a
solid, per unit mass.
Formally, let dV
denote an infinitesimal volume element within the deformed solid, and let denote the mass density (mass per unit
deformed volume). Suppose that the
element is subjected to a force . Then
The resultant body force
acting on any volume V within the deformed solid is
4.2 Traction acting on planes within a solid
Every
plane in the interior of a solid is subjected to a distribution of
traction. To see this, consider a
loaded, solid, body in static equilibrium.
Imagine cutting the solid in two.
The two parts of the solid must each be in static equilibrium. This is possible only if forces act on the
planes that were created by the cut.
 The internal
traction vector T(n) represents the force per unit area acting on a section
of the deformed body across a plane with outer normal vector n.
The internal
traction vector T(n) represents the force per unit area acting on a section
of the deformed body across a plane with outer normal vector n.
Formally,
let dA be an element of area in the
interior of the solid, with normal n. Suppose that the material on the underside of
dA is subjected to a force across the plane dA. Then
Note
that internal traction is the force per
unit area of the deformed solid, like `true stress’
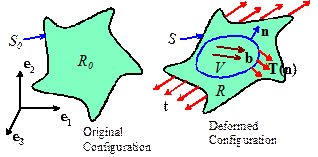
 The resultant force acting on any internal volume V with boundary surface A within a deformed solid is
The resultant force acting on any internal volume V with boundary surface A within a deformed solid is
The
first term is the resultant force acting on the internal surface A, the second term is the resultant body
force acting on the interior V.
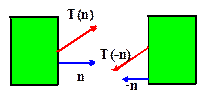
 Newton’s third law (every action has an equal and
opposite reaction) requires that
Newton’s third law (every action has an equal and
opposite reaction) requires that
To
see this, note that the forces acting on planes separating two adjacent volume
elements in a solid must be equal and opposite.
 Traction acting on different planes passing
through the same point are related, in order to satisfy Newton’s second law (F=ma).
Traction acting on different planes passing
through the same point are related, in order to satisfy Newton’s second law (F=ma).
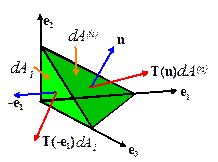 Let be a Cartesian basis. Let ,
,
denote the components of traction acting on
planes with normal vectors in the ,
,
and directions, respectively. Then, the traction components acting on a surface with normal n are given by
Let be a Cartesian basis. Let ,
,
denote the components of traction acting on
planes with normal vectors in the ,
,
and directions, respectively. Then, the traction components acting on a surface with normal n are given by
where are the components of n.
To see this, consider the forces acting on the infinitessimal
tetrahedron shown in the figure. The
base and sides of the tetrahedron have normals in the ,
and directions.
The fourth face has normal n. Suppose the volume of the tetrahedron is dV, and let , , , denote the areas of the faces. Assume that the material within the
tetrahedron has mass density and is subjected to a body force b. Let a denote the acceleration of the center of mass of the tetrahedron.
Then, F=ma for the tetrahedron requires that
Recall that
and divide through by :
Finally,
let . We can show that
so
or, using
index notation
The
significance of this result is that the tractions acting on planes with normals
in the ,
,
and directions completely characterize the
internal forces that act at a point.
Given these tractions, we can deduce the tractions acting on any other
plane. This leads directly to the
definition of the Cauchy stress tensor in the next section.
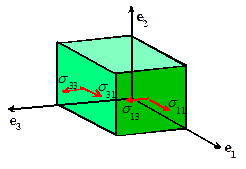
4.3 The Cauchy (true) stress tensor
Consider
a solid which deforms under external loading. Let be a Cartesian basis. Let ,
,
denote the components of traction acting on
planes with normals in the ,
,
and directions, respectively, as outlined in the
preceding section
 Define the components of the Cauchy stress tensor by
Define the components of the Cauchy stress tensor by
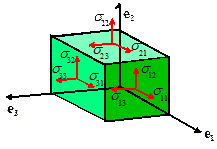
Then, the traction acting on any plane with normal n follows as
To see this, recall the
last result from the preceding section
and substitute for in terms of the components of the Cauchy
stress tensor
The
Cauchy stress tensor completely characterizes the internal forces acting in a
deformed solid. The physical
significance of the components of the stress tensor is illustrated in the figure:
represents the ith component of traction acting on a plane with normal in the direction.
Note the Cauchy stress represents force per unit area of the deformed solid. In elementary strength of materials courses
it is called `true stress,’ for this reason.
HEALTH WARNING: Some texts define stress as the transpose of the definition used here,
so that . In this case the first index for each stress
component denotes the direction of traction, while the second denotes the
normal to the plane. We will see later
that Cauchy stress is always symmetric, so there is no confusion if you use the
wrong definition. But some stress
measures are not symmetric (see
below) and in this case you need to be careful to check which convention the
author has chosen.
4.4 Other stress measures Kirchhoff, Nominal and Material stress tensors
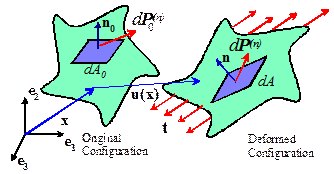 Cauchy stress (the actual force per unit area acting on an
actual, deformed solid) is the most physical measure of internal force. Other definitions of stress often appear in
constitutive equations, however.
Cauchy stress (the actual force per unit area acting on an
actual, deformed solid) is the most physical measure of internal force. Other definitions of stress often appear in
constitutive equations, however.
The
other stress measures regard forces as acting on the undeformed solid.
Consequently, to define them we must know not only what the deformed
solid looks like, but also what it looked like before deformation. The deformation is described by a
displacement vector and the associated deformation gradient
as outlined in Section 2.1.
In addition, let
We then define the
following stress measures
 Kirchhoff stress
Kirchhoff stress
 Nominal (First Piola-Kirchhoff) stress
Nominal (First Piola-Kirchhoff) stress
 Material
(Second Piola-Kirchhoff) stress
Material
(Second Piola-Kirchhoff) stress
The inverse relations are
also useful the one for Kirchhoff stress is obvious the others are
The Kirchoff stress has no obvious physical significance.
The
nominal stress tensor can be
regarded as the internal force per unit undeformed area acting within a solid,
as follows
1. Visualize an element of area dA in the deformed solid, with normal n, which is subjected to a force by the internal traction in the solid;
2. Suppose that the element of area dA has started out as an element of area with normal in the undeformed solid, as shown in the
figure;
3. Then, the force is related to the nominal stress by
To
see this, note that one can show that
Recall
that the Cauchy stress is defined so that
Substituting
for and rearranging shows that
The
material stress tensor can also be visualized
as force per unit undeformed area, except that the forces are regarded as
acting within the undeformed solid, rather than on the deformed solid. Specifically
1. The infinitesimal force is assumed to behave like an infinitesimal
material fiber in the solid, in the sense that it is stretched and rotated just
like an small vector dx in the solid
2.
This means that
we can define a (fictitious) force in the reference configuration that is related to by or .
3.
This fictitious
force is related to material stress by
To see this, substitute
into the expression relating to nominal stress to see that
Finally multiply through by
,
note ,
and rearrange to see that
where we have noted that
In
practice, it is best not to try to attach too much physical significance to
these stress measures. Cauchy stress is
the best physical measure of internal force it is the force per unit area acting inside
the deformed solid. The other stress
measures are best regarded as generalized
forces (in the sense of Lagrangian mechanics), which are work-conjugate to
particular strain measures. This means
that the stress measure multiplied by the time derivative of the strain measure
tells you the rate of work done by the forces.
When setting up any mechanics problem, we always work with conjugate
measures of motion and forces.
Specifically,
we shall show later that the rate of work done by stresses acting on a small material
element with volume in the undeformed solid (and volume in the deformed solid) can be computed as
where
is the stretch rate tensor, is the rate of change of deformation gradient,
and is the rate of change of Lagrange strain
tensor. Note that Cauchy stress (and
also Kirchhoff stress) is not conjugate to any convenient strain measure this is the main reason that nominal and
material stresses need to be defined.
The nominal stress is conjugate to the deformation gradient, while the
material stress is conjugate to the Lagrange strain tensor.
4.5 Stress measures for
infinitesimal deformations
For
a problem involving infinitesimal
deformation (where shape changes are characterized by the infinitesimal
strain tensor and rotation tensor) all the stress measures defined in the
preceding section are approximately equal.
To
see this, write the deformation gradient as ;
recall that ,
and finally assume that for infinitesimal motions . Substituting into the formulas relating
Cauchy stress, Nominal stress and Material stress, we see that
The same procedure will show that material stress
and Cauchy stress are approximately equal, to within a term of order
4.6 Principal
Stresses and directions
For any stress measure, the principal stresses and their directions ,
with i=1..3 are defined such that
Clearly,
- The
principal stresses are the (left) eigenvalues of the stress tensor
- The principal
stress directions are the (left) eigenvectors of the stress tensor
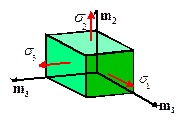 The term `left’ eigenvector and eigenvalue indicates
that the vector multiplies the tensor on the left. We will see later that
Cauchy stress and material stress are both symmetric. For a symmetric tensor the left and right
eigenvalues and vectors are the same.
The term `left’ eigenvector and eigenvalue indicates
that the vector multiplies the tensor on the left. We will see later that
Cauchy stress and material stress are both symmetric. For a symmetric tensor the left and right
eigenvalues and vectors are the same.
Note that the
eigenvectors of a symmetric tensor are orthogonal. Consequently, the principal Cauchy or
material stresses can be visualized as tractions acting normal to the faces of
a cube. The principal directions specify the orientation of this special cube.
One can also show that if ,
then is the largest normal traction acting on any
plane passing through the point of interest, while is the lowest.
This is helpful in defining damage criteria for brittle materials, which
fail when the stress acting normal to a material plane reaches a critical
magnitude.
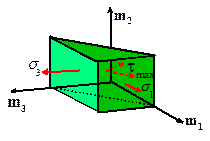
In
the same vein, the largest shear stress can be shown to act on the plane with
unit normal vector (at 45o to the and axes), and its magnitude is . This observation is useful for defining yield
criteria for metal polycrystals, which begin to deform plastically when the
shear stress acting on a material plane reaches a critical value.
4.7 Hydrostatic and Deviatoric Stress; von Mises
effective stress
Given the Cauchy stress tensor
,
the following may be defined:
The Hydrostatic stress is defined as
The Deviatoric stress tensor is defined as
The Von-Mises effective stress is defined
as
The
hydrostatic stress is a measure of
the pressure exerted by a state of stress.
Pressure acts so as to change the volume of a material element.
The
deviatoric stress is a measure of the
shearing exerted by a state of stress. Shear stress tends to distort a solid,
without changing its volume.
The
Von-Mises effective stress can be
regarded as a uniaxial equivalent of a multi-axial stress state. It is used in many failure or yield
criteria. Thus, if a material is known
to fail in a uniaxial tensile test (with the only nonzero stress component) when ,
it will fail when under multi-axial loading (with several )
The hydrostatic stress and von Mises stress can also
be expressed in terms of principal stresses as
The hydrostatic and von
Mises stresses are invariants of the
stress tensor they have the same value regardless of the
basis chosen to define the stress components.
4.8 Stresses near an external surface or edge boundary conditions on stresses
Note
that at an external surface at which
tractions are prescribed, some components of stress are known. Specifically, let n denote a unit vector normal to the surface, and let t denote the traction (force per unit
area) acting on the surface. Then the
Cauchy stress at the surface must satisfy
For
example, suppose that a surface with normal in the direction is subjected to no loading. Then (noting
that ) it follows that .
In addition, two of the principal stress directions must be parallel to the
surface; the third (with zero stress) must be perpendicular to the surface.
The
stress state at an edge is even simpler.
Suppose that surfaces with normals in the and are traction free. Then ,
so that 6 stress components are known to be zero.
 4.1 Surface traction and internal body force
4.1 Surface traction and internal body force
![]() The surface
traction vector t at a point
on the surface represents the force acting on the surface per unit area of the
deformed solid.
The surface
traction vector t at a point
on the surface represents the force acting on the surface per unit area of the
deformed solid. ![]()


![]() The body
force vector denotes the external force acting on the interior of a
solid, per unit mass.
The body
force vector denotes the external force acting on the interior of a
solid, per unit mass.

![]() The internal
traction vector T(n) represents the force per unit area acting on a section
of the deformed body across a plane with outer normal vector n.
The internal
traction vector T(n) represents the force per unit area acting on a section
of the deformed body across a plane with outer normal vector n.
![]() The resultant force acting on any internal volume V with boundary surface A within a deformed solid is
The resultant force acting on any internal volume V with boundary surface A within a deformed solid is
![]()
![]() Traction acting on different planes passing
through the same point are related, in order to satisfy
Traction acting on different planes passing
through the same point are related, in order to satisfy  Let be a Cartesian basis. Let ,
,
denote the components of traction acting on
planes with normal vectors in the ,
,
and directions, respectively. Then, the traction components acting on a surface with normal n are given by
Let be a Cartesian basis. Let ,
,
denote the components of traction acting on
planes with normal vectors in the ,
,
and directions, respectively. Then, the traction components acting on a surface with normal n are given by![]() Define the components of the Cauchy stress tensor by
Define the components of the Cauchy stress tensor by
 Cauchy stress (the actual force per unit area acting on an
actual, deformed solid) is the most physical measure of internal force. Other definitions of stress often appear in
constitutive equations, however.
Cauchy stress (the actual force per unit area acting on an
actual, deformed solid) is the most physical measure of internal force. Other definitions of stress often appear in
constitutive equations, however. ![]() Kirchhoff stress
Kirchhoff stress ![]() Nominal (First Piola-Kirchhoff) stress
Nominal (First Piola-Kirchhoff) stress ![]() Material
(Second Piola-Kirchhoff) stress
Material
(Second Piola-Kirchhoff) stress  The term `left’ eigenvector and eigenvalue indicates
that the vector multiplies the tensor on the left. We will see later that
Cauchy stress and material stress are both symmetric. For a symmetric tensor the left and right
eigenvalues and vectors are the same.
The term `left’ eigenvector and eigenvalue indicates
that the vector multiplies the tensor on the left. We will see later that
Cauchy stress and material stress are both symmetric. For a symmetric tensor the left and right
eigenvalues and vectors are the same.

