Vibrations
5.1 Overview of Vibrations
5.1.1 Examples of practical vibration problems
Vibration is a continuous cyclic motion of a structure or a component.
Generally, engineers try to avoid vibrations, because vibrations have a number of unpleasant effects:
· Cyclic motion implies cyclic forces. Cyclic forces are very damaging to materials.
· Even modest levels of vibration can cause extreme discomfort;
· Vibrations generally lead to a loss of precision in controlling machinery.
Examples where vibration suppression is an issue include:

Structural vibrations. Most buildings are mounted on top of special rubber pads, which are intended to isolate the building from ground vibrations. The figure on the right shows vibration isolators being installed under the floor of a building during construction (from www.wilrep.com )
No vibrations course is complete without a mention of the Tacoma Narrows suspension bridge. This bridge, constructed in the 1940s, was at the time the longest suspension bridge in the world. Because it was a new design, it suffered from an unforseen source of vibrations. In high wind, the roadway would exhibit violent torsional vibrations, as shown in the picture below.


You can watch newsreel footage of the
vibration and even the final collapse at http://www.youtube.com/watch?v=HxTZ446tbzE
To the credit of the designers, the bridge survived for an amazingly
long time before it finally failed. It is thought that the vibrations were a form
of self-excited vibration known as `flutter,’ or ‘galloping’ A similar form of vibration is known to occur
in aircraft wings.
Interestingly, modern cable stayed bridges that also suffer from a new
vibration problem: the cables are very lightly damped and can vibrate badly in
high winds (this is a resonance problem, not flutter). You can find a detailed
article on the subject at www.fhwa.dot.gov/bridge/pubs/05083/chap3.cfm. Some bridge designs
go as far as to incorporate active vibration suppression systems in their
cables.
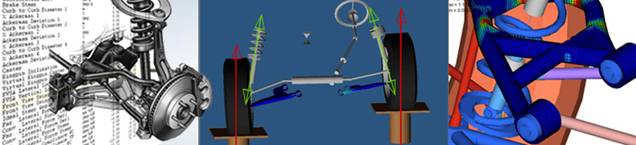
 Vehicle
suspension systems are familiar to everyone, but continue to evolve as
engineers work to improve vehicle handling and ride (the figure above is from http://www.altairhyperworks.com. A radical
new approach to suspension design emerged in 2003 when a research group led by
Malcolm Smith at Cambridge University invented a new mechanical suspension
element they called an ‘inerter’. This
device can be thought of as a sort of generalized spring, but instead of
exerting a force proportional to the relative displacement of its two ends, the
inerter exerts a force that is proportional to the relative acceleration of its two ends. An actual realization is shown in the
figure. You can find a detailed
presentation on the theory behind the device at http://www-control.eng.cam.ac.uk/~mcs/lecture_j.pdf The device was adopted in secret by the McLaren
Formula 1 racing team in 2005 (they called it the ‘J damper’, and a scandal
erupted in Formula 1 racing when the Renault team managed to steal drawings for
the device, but were unable to work out what it does. The patent for the device has now been
licensed Penske and looks to become a standard element in formula 1
racing. It is only a matter of time
before it appears on vehicles available to the rest of us.
Vehicle
suspension systems are familiar to everyone, but continue to evolve as
engineers work to improve vehicle handling and ride (the figure above is from http://www.altairhyperworks.com. A radical
new approach to suspension design emerged in 2003 when a research group led by
Malcolm Smith at Cambridge University invented a new mechanical suspension
element they called an ‘inerter’. This
device can be thought of as a sort of generalized spring, but instead of
exerting a force proportional to the relative displacement of its two ends, the
inerter exerts a force that is proportional to the relative acceleration of its two ends. An actual realization is shown in the
figure. You can find a detailed
presentation on the theory behind the device at http://www-control.eng.cam.ac.uk/~mcs/lecture_j.pdf The device was adopted in secret by the McLaren
Formula 1 racing team in 2005 (they called it the ‘J damper’, and a scandal
erupted in Formula 1 racing when the Renault team managed to steal drawings for
the device, but were unable to work out what it does. The patent for the device has now been
licensed Penske and looks to become a standard element in formula 1
racing. It is only a matter of time
before it appears on vehicles available to the rest of us.
 Precision
Machinery: The picture on the right shows one example of a
precision instrument. It is essential
to isolate electron microscopes from vibrations. A typical transmission electron microscope is
designed to resolve features of materials down to atomic length scales. If the specimen vibrates by more than a few
atomic spacings, it will be impossible to see!
This is one reason that electron microscopes are always located in the
basement
Precision
Machinery: The picture on the right shows one example of a
precision instrument. It is essential
to isolate electron microscopes from vibrations. A typical transmission electron microscope is
designed to resolve features of materials down to atomic length scales. If the specimen vibrates by more than a few
atomic spacings, it will be impossible to see!
This is one reason that electron microscopes are always located in the
basement the basement of a building vibrates much less
than the upper floors. Professor K.-S. Kim at Brown recently invented
and patented a new vibration isolation system to support his atomic force
microscope on the 7th floor of the Barus-Holley building
you can find the patent at United
States Patent, Patent Number 7,543,791.
Here is another precision instrument that is very sensitive to vibrations.
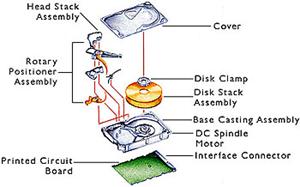 The picture shows features of a typical hard disk
drive. It is particularly important to
prevent vibrations in the disk stack assembly and in the disk head positioner,
since any relative motion between these two components will make it impossible
to read data. The spinning disk stack assembly has some very interesting
vibration characteristics (which fortunately for you, is beyond the scope of
this course).
The picture shows features of a typical hard disk
drive. It is particularly important to
prevent vibrations in the disk stack assembly and in the disk head positioner,
since any relative motion between these two components will make it impossible
to read data. The spinning disk stack assembly has some very interesting
vibration characteristics (which fortunately for you, is beyond the scope of
this course).
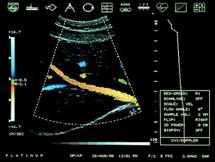 Vibrations are not always undesirable, however. On occasion, they can be put to good
use. Examples of beneficial applications
of vibrations include ultrasonic probes, both for medical application and for
nondestructive testing. The picture shows a
medical application of ultrasound: it is an image of someone’s colon. This type of instrument can resolve features
down to a fraction of a millimeter, and is infinitely preferable to exploratory
surgery. Ultrasound is also used to
detect cracks in aircraft and structures.
Vibrations are not always undesirable, however. On occasion, they can be put to good
use. Examples of beneficial applications
of vibrations include ultrasonic probes, both for medical application and for
nondestructive testing. The picture shows a
medical application of ultrasound: it is an image of someone’s colon. This type of instrument can resolve features
down to a fraction of a millimeter, and is infinitely preferable to exploratory
surgery. Ultrasound is also used to
detect cracks in aircraft and structures.
Musical instruments and loudspeakers are a second example of systems which put vibrations to good use. Finally, most mechanical clocks use vibrations to measure time.
5.1.2 Vibration Measurement
 When faced with a vibration problem, engineers
generally start by making some measurements to try to isolate the cause of the
problem. There are two common ways to
measure vibrations:
When faced with a vibration problem, engineers
generally start by making some measurements to try to isolate the cause of the
problem. There are two common ways to
measure vibrations:
1. An accelerometer is a small electro-mechanical device that gives an electrical signal proportional to its acceleration. The picture shows a typical 3 axis accelerometer.
2. A displacement transducer is similar to an accelerometer, but gives an electrical signal proportional to its displacement.
Displacement transducers are generally preferable if you need to measure low frequency vibrations; accelerometers behave better at high frequencies.
The most common procedure is to mount three accelerometers at a point on the vibrating structure, so as to measure accelerations in three mutually perpendicular directions. The velocity and displacement are then deduced by integrating the accelerations.
5.1.3 Features of a Typical Vibration Response
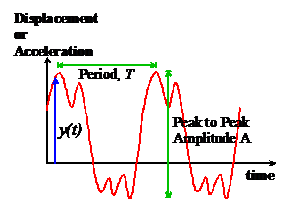 The picture below shows a typical signal that you
might record using an accelerometer or displacement transducer.
The picture below shows a typical signal that you
might record using an accelerometer or displacement transducer.
Important features of the response are
![]() The signal is
often (although not always) periodic:
that is to say, it repeats itself at fixed intervals of time. Vibrations that do not repeat themselves in
this way are said to be random. All the systems we consider in this course
will exhibit periodic vibrations.
The signal is
often (although not always) periodic:
that is to say, it repeats itself at fixed intervals of time. Vibrations that do not repeat themselves in
this way are said to be random. All the systems we consider in this course
will exhibit periodic vibrations.
![]() The PERIOD of the signal, T, is the time required for
one complete cycle of oscillation, as shown in the picture.
The PERIOD of the signal, T, is the time required for
one complete cycle of oscillation, as shown in the picture.
![]() The FREQUENCY of
the signal, f, is the number of cycles of oscillation per
second. Cycles per second is often given the name Hertz: thus, a signal which
repeats 100 times per second is said to oscillate at 100 Hertz.
The FREQUENCY of
the signal, f, is the number of cycles of oscillation per
second. Cycles per second is often given the name Hertz: thus, a signal which
repeats 100 times per second is said to oscillate at 100 Hertz.
![]() The ANGULAR
FREQUENCY of the signal,
The ANGULAR
FREQUENCY of the signal, ,
is defined as
.
We specify angular frequency in radians per second. Thus, a signal that oscillates at 100 Hz has
angular frequency
radians per second.
![]() Period, frequency
and angular frequency are related by
Period, frequency
and angular frequency are related by
![]() The PEAK-TO-PEAK
AMPLITUDE of the signal, A, is the difference between its maximum value and
its minimum value, as shown in the picture
The PEAK-TO-PEAK
AMPLITUDE of the signal, A, is the difference between its maximum value and
its minimum value, as shown in the picture
![]() The AMPLITUDE
of the signal is generally taken to mean half its peak to peak amplitude.
Engineers sometimes use amplitude as an abbreviation for peak to peak
amplitude, however, so be careful.
The AMPLITUDE
of the signal is generally taken to mean half its peak to peak amplitude.
Engineers sometimes use amplitude as an abbreviation for peak to peak
amplitude, however, so be careful.
![]() The ROOT MEAN
SQUARE AMPLITUDE or RMS amplitude is defined as
The ROOT MEAN
SQUARE AMPLITUDE or RMS amplitude is defined as
5.1.4 Harmonic Oscillations
Harmonic oscillations are a particularly simple form
of vibration response. Consider the
spring-mass system shown below (you will only see the spring-mass system if
your browser supports Java). If the
spring is perturbed from its static equilibrium position, it vibrates (press
`start’ to watch the vibration). We will
analyze the motion of the spring mass system soon. We will find that the
displacement of the mass from its static equilibrium position, ,
has the form
Here, is
the amplitude of the displacement,
is the frequency of oscillations in radians
per second, and
(in radians) is known as the `phase’ of the
vibration. Vibrations of this form are
said to be Harmonic.
Typical values for amplitude and frequency are listed in the table below
|
|
Frequency /Hz |
Amplitude/mm |
|
Atomic Vibration |
|
|
|
Threshold of human perception |
1-8 |
|
|
Machinery and building vibes |
10-100 |
|
|
Swaying of tall buildings |
1-5 |
10-1000 |
We can also express the displacement in terms of its period of oscillation T
The velocity and acceleration
of the mass follow as
Here, is the amplitude of the velocity, and
is the amplitude of the acceleration. Note the simple relationships between
acceleration, velocity and displacement amplitudes.
Experiment with the Java applet shown until you feel comfortable with the concepts of amplitude, frequency, period and phase of a signal.
Surprisingly, many complex engineering systems behave just like the spring mass system we are looking at here. To describe the behavior of the system, then, we need to know three things (in order of importance):
(1) The frequency (or period) of the vibrations
(2) The amplitude of the vibrations
(3) Occasionally, we might be interested in the phase, but this is rare.
So, our next problem is to find a way to calculate these three quantities for engineering systems.
We will do this in stages. First, we will analyze a number of freely vibrating, conservative systems. Second, we will examine free vibrations in a dissipative system, to show the influence of energy losses in a mechanical system. Finally, we will discuss the behavior of mechanical systems when they are subjected to oscillating forces.
