
Division of Engineering
Brown University
2.2 Using Newton’s laws to calculate accelerations and forces
We are now in a position to state Newton’s first and second laws mathematically.
![]()
We can use this information to solve two types of problem: given the force acting on a particle, we can deduce its acceleration. Alternatively, we can calculate the force acting on a particle whose position, velocity or acceleration are given as a function of time.
We use the following general procedure to solve problems like this
(1) Decide how to idealize the system (as one or more particles)
(2) Draw a free body diagram showing the forces acting on each particle
(3) Consider the kinematics of the problem. Can you write down the magnitude and/or direction of the acceleration of any of the particles? Can you relate the accelerations of two particles? (e.g. two particles might move together, in which case their accelerations must be equal)
(4) Write down F=ma for each particle
(5) Solve the resulting equations for any unknown components of force or acceleration.
Its best to show how this is done by means of examples.
Example 1: Suppose you are in an elevator and standing on a set of scales. When the elevator is stationary, the scales read your weight, W.
(a) What is the acceleration of the elevator of the scales read 1.01W?
We will follow the standard procedure:
Here is a free body diagram for the scales and for the person standing on the scales
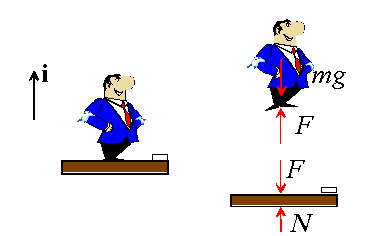
we have assumed that the gravitational force acting on the scales is negligible. Note how reaction forces have been denoted by an unknown value, which we will need to calculate later.
Now we consider kinematics. We know the elevator moves vertically, so
the direction of the acceleration must be along the i direction,
but we don’t know its magnitude. We therefore denote the acceleration
of the elevator (and everything in it) by ![]() , where a is
a scalar to be found.
, where a is
a scalar to be found.
Now we write down Newton’s second law for the person
Finally, we know that the scales record the force F. When the elevator is stationary, a=0 and therefore F=mg. When the elevator is accelerating, the force must be 1.01mg. Therefore
whence
Example 2: The masses ![]() ,
, ![]() , and the coefficients
of friction between all of the surfaces are
, and the coefficients
of friction between all of the surfaces are ![]() ,
, ![]() . What is the
largest force F that can be applied without causing A to
slip relative to B? What is the resulting acceleration?
. What is the
largest force F that can be applied without causing A to
slip relative to B? What is the resulting acceleration?

Draw free body diagrams for both masses, and also for the two masses together. We have to be careful to account for the friction forces correctly. Note that if there is no slip between two contacting surfaces, we don’t need to worry about the direction of the friction force, since the sign of the force can be positive or negative. If there is sliding between the contacting surfaces, we need to make sure that the friction force opposes sliding.
We will assume that A does not slip relative to B, since we are interested in finding the largest F for this to be possible.
We will assume that the block B is sliding to the right, since this gives the largest value for F (if this isn’t obvious to you, you have to solve the problem twice, to see which direction of sliding gives the biggest F).

Geometrical considerations show us that:
(i) The acceleration of both masses must be equal (because they move together if there’s no sliding between A and B)
(ii) The acceleration must be in the i direction (because the masses move horizontally)
Let us denote the acceleration (of both masses) by
Hence, apply Newton II to mass A alone:
Apply Newton II to both masses together
The friction law requires
(A is sticking to B, so we use the static friction coefficient. B is sliding along the ground, so we use the kinetic friction coefficient.)
The j component of eq. (1) shows that ![]()
Hence, the i component of eq. (1), together with the first of
eq. (3) shows that ![]()
The j component of eq. (2) shows that ![]()
Hence, the i component of (2) together with the second of (3) and our result for acceleration shows that
Substituting the numerical values given shows
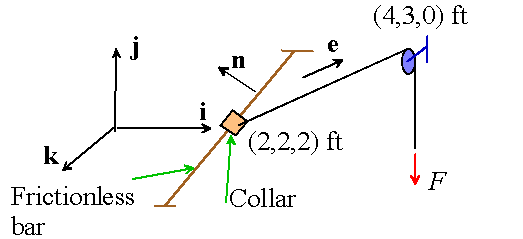
Example 3: The acceleration of the 20lb collar A is ![]() .
What is the force F? Friction may be neglected.
.
What is the force F? Friction may be neglected.
To solve this problem, we need to know something about pulleys. Suppose an inextensible cable passes over a pulley, as shown below

If the pulley has negligible mass (or, more precisely, negligible moment of inertia about its axis of rotation), or if the pulley is not rotating (i.e. the rope is stationary), the tension in the cable must be the same on both sides of the pulley. This issue will be discussed in more detail when we cover rigid body dynamics.
Consequently, the collar is subjected to three forces: (i) a force F acting along the direction of the cable; (ii) a reaction force of unknown magnitude R from the bar on which it slides. Since the bar is frictionless, we know that the reaction force must act normal to the bar; (iii) a vertical gravitational force.
We need to describe this force as a vector. Let n be a unit vector normal to the smooth bar (we don’t need to calculate n). Let e be a unit vector parallel to the cable. We can construct e from the information in the picture. Note that
is the position vector of the pulley relative to the collar. Therefore, a unit vector in this direction is
Therefore, the resultant force acting on the collar is given by
Now, apply Newton II:
To solve this for F, note that the direction of a must
be parallel to the bar (the collar slides up and down the bar, therefore
its velocity and acceleration vectors are parallel to the bar). Therefore,
![]() , since a and n are mutually perpendicular.
Therefore, taking the dot product of both sides with a and rearranging
gives
, since a and n are mutually perpendicular.
Therefore, taking the dot product of both sides with a and rearranging
gives
Substituting numerical values
Example 4: Two weights of mass ![]() and
and ![]() are connected
by a cable passing over two freely rotating pulleys as shown. Find an expression
for the tension in the cable connecting the two weights.
are connected
by a cable passing over two freely rotating pulleys as shown. Find an expression
for the tension in the cable connecting the two weights.
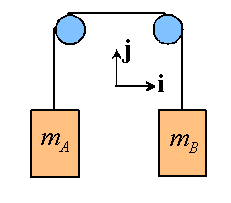
Start, as usual, with a free body diagram for each mass
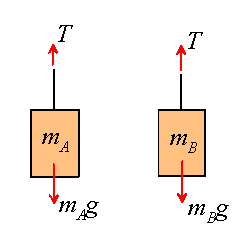
Notice that we have used the condition that the tension must be equal along the entire length of the cable.
Now, consider kinematics. We know that both masses must move in the j direction. We also know that the masses always move at the same speed but in opposite directions. Therefore, their accelerations must be equal and opposite. We can express this mathematically as
Now, write down Newton’s second law for each mass
We now have three equations for three unknowns (the unknowns are ![]() and
T).
and
T).
To solve them, first substitute for ![]() in the last equation
in terms of
in the last equation
in terms of ![]() :
:
Now, solve these two equations for T:
With the numbers given, T=11.8N
We can also calculate the acceleration of the masses