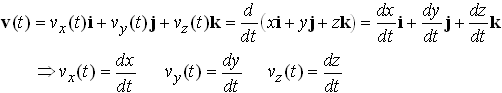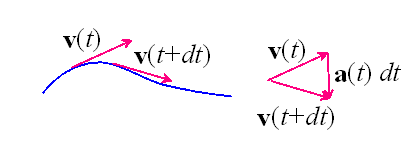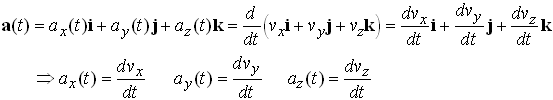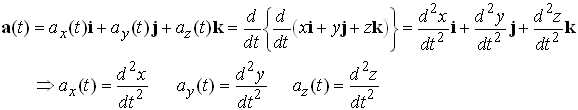EN4: Dynamics and Vibrations
          

 

Division of Engineering
   Brown University

 

2. Motion of Particles

In this section, we will develop techniques to predict the motion of particles. Three issues will be explored: (i) we will formally define measures of position, velocity and acceleration for particles (ii) we will explore techniques for deducing velocity and position, given acceleration and (iii) we will see how to predict the motion of particles using Newton’s laws of motion.

 

 

2.1 Vector definitions of position, velocity and acceleration

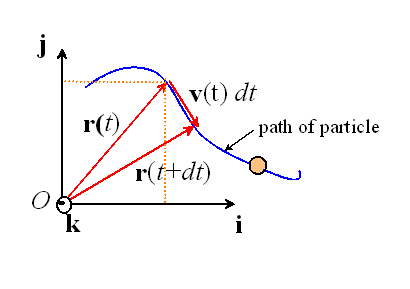
To describe motion, we first need to adopt an `intertial reference frame.’ This means we agree to take some point in our system as being fixed, and agree on three directions, which do not vary in time. In the picture shown, O is fixed, and the unit vectors {i,j,k} specify three directions which do not vary with time.

Consider a particle, which moves along some prescribed path.

The position of the particle is defined by the position vector r(t), which specifies the distance and direction of the particle relative to the fixed point O. Because the particle is moving, the vector varies with time.

We normally express position vectors as components in a basis, i.e.

To write down position vectors, follow exactly the same procedure as you used to solve statics problems in EN3.

The velocity of a particle is defined as the time derivative of its position. Derivatives of vectors are defined by exactly the same limit process as derivatives of scalars:

You can visualize the velocity as follows. Consider the particle shown in the picture above. Suppose that, at time t, the particle is at a position r(t). Now, look at the particle again an instant dt later. Its position is now r(t+dt). The little vector from r(t) to r(t+dt) is v(t)dt, as shown in the picture.

Two very important and useful observations:

The direction of the velocity vector is always tangent to the path of the particle

The magnitude of the velocity vector is the distance (arc length) travelled along the path per unit time.

If the position vector of a particle is specified as components in a fixed basis (i.e. the basis vectors {i,j,k} do not vary with time), it is easy to calculate the velocity of the particle

Finally, the acceleration of a particle is defined as the time derivative of its velocity

It is generally much more difficult to visualize accelerations than either position or velocity, but let’s give it a try. Consider a particle, which moves along the blue curve shown.

We know the velocity vector is always tangent to the curve.

Thus, the velocity at time t and an instant later at t+dt might look like the arrows shown in the picture. The vector from v(t) to v(t+dt) is a(t)dt, as shown in the picture.

Note that a particle is accelerating if either

(i) it is travelling along a straight line, but its speed is changing;

(ii) it is travelling at constant speed, but is moving along a curved path (this is because the direction of the velocity is changing, even though its magnitude is fixed)

(iii) both its speed and direction of travel are changing.

A major objective of this section of the course is to help you to get a feel for the accelerations associated with various types of motion.

If the position or velocity of a particle is specified as components in a fixed basis, it is straightforward to calculate the acceleration. In terms of velocity:

Alternatively, in terms of position