EN4 : Dynamics and Vibrations
The planets and stars have amazed humans for thousands of years. The laws of classical physics were discovered, essentially, through a study of the motion of planets. Before the time of Copernicus, it was believed that the earth was the center of the universe and that all other bodies revolved around earth. These ideas were dramatically overthrown when Kepler, after a thorough study of observations made by Brahe, stated his famous laws of planetary motion. They are
Newton proved these laws using his laws of motion, and the ``Universal Law of
Gravitation'' which he discovered. We will start our discussion on central force motion
with a statement of the law of gravitation. Consider two bodies of mass 
and 
, separated by a distance r. The law
of gravitation states that the bodies attract each other with a force of
magnitude
and directed along the line joining the two bodies. The factor G is a universal
constant which is equal to 6.673 
m 
/kg 
s 
. The discovery of this law by Newton is an
important milestone in the history of physics.
Back to our solar system, let us consider the motion of a planet around the Sun. Let M
be the mass of the Sun and m that of the planet. Clearly 
, for example, the Sun is about 330,000
times as massive as the earth. Thus we may approximate the Sun as being at rest and that
the planet moves around the Sun under the influence of the force of gravitation that the
Sun exerts on the planet. Thus the force acting on the planet is always directed towards
the Sun. Such a motion is called central force motion, where the force acting on
a particle is always directed towards a point, in our case the Sun.
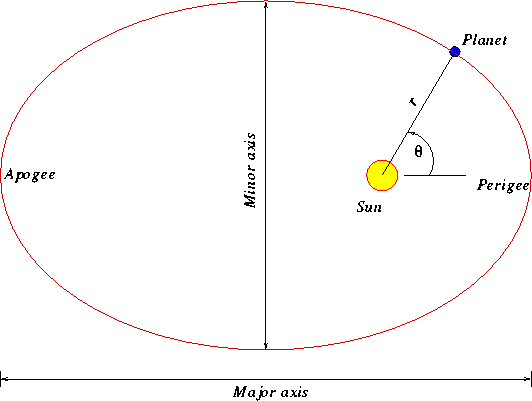
To describe motion of planets around the Sun, let us use a polar coordinate system
centered around the Sun. Thus the position of the planet will be described by polar
coordinates 
. Kepler's
first law tells you that the planet moves around in an elliptic orbit. Before we proceed
with our discussion we have to learn some terminology regarding orbits. They are major-axis
which is the ``longer diameter'' of the ellipse, minor-axis which is the
``shorter diameter'' of the ellipse, perigee which is the point on the ellipse
where the planet come closest to the Sun, apogee which is the point on the orbit
where the planet is farthest from the Sun.
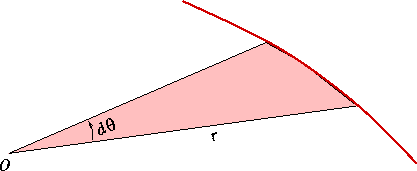
Having learned the terminology, let us now prove Kepler's second law. Using the polar
coordinate system that we had set up, let us compute the rate at which area is swept out.
In a small time dt, let the angle change by an amount 
. From the figure, we can then compute what
area of the small triangle that was swept out in the small time interval dt as 
. Thus
Good! May be you see by now how to prove that 
is a constant. If you do not, read on.
Let us see what ``Angular Newton's Law'' has to say about the motion of the planet around the Sun. We know that the force that the Sun exerts on the planet is directed towards O. Well, then the moment of the force about the point O vanishes which means the angular momentum of the planet is conserved! Let us compute the angular momentum about O. This is
Thus we get that 
is
a constant. Since the mass of the planet is a constant we get that 
is a constant which is nothing but twice
the rate at which area is swept out by the planet. We have managed to prove Kepler's
second law based on very simple arguments! Kepler did not know about angular momentum - he
found this by painful calculations.
The other laws of Kepler can also be proved using what we have learned so far, but they involve some additional mathematics which I do not want to get into. If you are interested in planetary motion, read pages 230 to 234 of Meriam and Kreig.
Having introduced the gravitational force, let us now look at this from the point of view of energy conservation. The first question that comes to mind is ``is the force of gravity a conservative force?''. The answer is a resounding ``yes''. What is the potential energy function? In the case of our Sun-planet system, the potential energy function is
Note that the force on the planet can be gotten as 
. Note also that the potential energy is
always negative. In fact as 
the value of the potential energy goes to zero. In other words, the zero
for the energy is fixed at 
. As 
,
we see that 
. Since our
system is a conservative system, the total energy is conserved, or
is a constant. Note that in writing the total energy we have neglected the kinetic energy of the Sun. This is reasonable since we are assuming that the Sun, a star, is stationary and not affected by a mere planet.
We can put the idea of energy conservation to use in the following example.
Example 1: A rocket of mass m is located on the surface of earth. Find the minimum speed v of the rocket for it to completely escape from earth's gravitational field. This speed is called the ``escape velocity''.
Let A be the configuration where the rocket is located on the surface of the
earth (with speed v, and 
, 
is
the radius of the earth), and B is when the rocket is very far away form earth with
no velocity. The energy is configuration A is
where 
is the mass of
the earth and that in B is
By conservation of energy, we have that 
which means
If you plug in the numbers, you would get v = 11.2km/s. Thus is a body has a
speed 11.2km/s on the surface of the earth, it will escape to infinity.