EN4 : Dynamics and Vibrations
Thus far in this chapter, in treating motions of particles, our strategy has been to completely isolate the particle and write out all the forces that act on the particle. Let us look at this in a slightly different way. Consider holding a book in your hand at about your chest level. Now slowly raise the book above to a level above your head. To do this you had to apply a force on the book, and move it through a distance. If we apply the work-energy theorem of the previous sections naively, we will reach a rather absurd result. Here, then, is the argument: The work done by me should equal to the change in kinetic energy of the book, and therefore if I lift the book to a level above my head, I have done work and the book must go flying off. But if you try this (if you have never done this before), you will see that the book does not fly off. We came to an absurd conclusion because we did not account for the force of gravity on the book. But you can ask a very legitimate question: I know that I spent some effort in lifting the book, what happened to the work that I did?
To answer this question, we introduce the concept of potential energy. Potential energy is the energy possessed by a system that depends on the configuration of the system. For example, in the case of the book that we discussed above, book along with the earth is taken as the system. There is a potential energy associated with the book which is a function of the position of the book with respect to the ground (or the earth). When you lifted the book, the work that you did went into increasing the potential energy of the book, and none of the work that you did went to increasing the kinetic energy of the book.
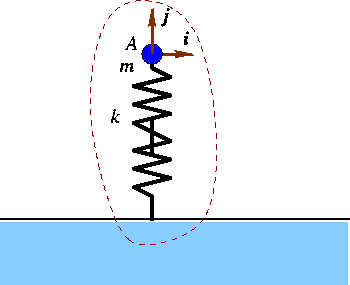
The above explanation might give you an intuitive understanding of the idea of potential energy. However, you might have realized that the ideas developed in the previous sections have to be refined to include the idea of potential energy. Let us pursue this point. We had said earlier that ``potential energy is the energy possessed by a system that depends on the configuration of the system''. The key ideas in that statement is that of a system and that of a configuration. The main step in talking about the potential energy is to identify the system of interest, and the parameters that describe the configuration of the system. Once these steps are taken, the next step is to write down a functional form for the potential energy of the system as a function of the configurational parameter. This last step is the most difficult one. Let us try to perform this task for our system consisting of the book which we shall idealize as a point particle with mass m.
The system of interest is shown by the dotted line, and includes the point particle and
the earth. The configurational parameter is the elevation of the particle above the
surface of the earth given by the coordinate y. Our next task is to write an
expression for the potential energy which we shall do now. Remember that we had developed
the following intuition: The work done by the force that you apply in lifting the book
(very slowly, i.e., keeping the book stationary at all times) is equal to the change in
the potential energy of the book. Let the force that you apply be 
. If we now isolate the particle, we know
that 
since the particle
is assumed to be stationary at all times. Thus 
. If you now go from a point with coordinate
to a point 
, we see that work that you
do in applying the force is
This, by our intuitive arguments, must be equal to the change in the potential energy of the system. Thus
Note that this quantity depends only on the elevation y. If we assume that 
i.e., we are agreeing to
assume that the potential energy is zero when y=0, we get that the potential energy
of the system consisting of the book and the earth can be written as
Two very important things can be inferred from this expression for the potential energy:
) and the expression for the
gravitational potential energy, we see that 
The symbol 
stands
for the ``gradient'' of the scalar field and is defined as
to the
point 
. This is 
where 
and 
are the values of the
potential energy at the points B and A respectively. Here is the punch-line;
The work done by gravity in going from point A to B does not depend on
the path! Also if A coincides with B the work done by gravity vanishes. In
other words, the work done by the force of gravity in a closed path is zero.
These two essential features are interrelated, as will be seen later.
Let us now consider another problem. Here we will look at a spring mass system and formulate the potential energy of this system. We will see that both the features that we noted in the case of the gravitational example above are available in this system as well.
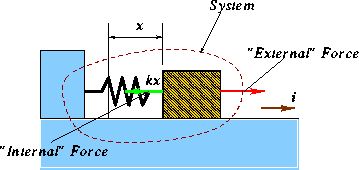
To this end, consider the spring mass system (no frictional effects are present). As
before, our first step will be to identify the system, and a parameter that describes the
configuration of the system. The system will include the spring and the mass together as
shown by the dotted line. To find and expression for the potential energy, imagine that
you apply a force as
shown in the figure. The key idea is again to compute the work done in stretching the
sprint through a distance x very slowly such that the system is in
equilibrium at all times. This implies that if the spring is extended by a distance 
, y will have that the 
for equilibrium or 
. Now compute the work that you
do i.e., the work done by the force in stretching the spring through a distance x:
Again, this must go into changing the potential energy of the system. In other words,
Again, taking the value of the potential energy of the system to be zero when the spring is unstretched, we find that
Again, one can easily see that the force exerted by the spring on the block can be derived from the expression of the potential energy as
Again, you will be able to show that the work done by the spring force in going between two points does not depend on the path taken in going from the two points. These two features are common in both the problems that we have looked at.
In science, we make generalizations based on our experience of few instances. The test of such generalizations is, always, experiment. Following this logic, let us make a generalization.
represents the configuration of a system, one can define the potential
energy of a system as a scalar function of this configuration parameter. Let us call this 
. 
(note that
there might be other forces that act on the particle). 
in going from a configuration A to B will not depend on the
path taken in going from point A to B. Also the work done in going through a
closed path always vanishes. Now lets ask the following question: If someone gives you a force field, i.e., 
, how do you tell if there
is a potential energy associated with that force? The answer is that the work done in
every closed path must be zero, or,
Another way to characterize this is that
or the curl of the force field vanishes. Force fields which are associated with a potential (whose curl vanishes everywhere) are of fundamental importance in physics and are called conservative forces. Examples of conservative forces are spring forces, gravity, electro-static force etc. Examples of nonconservative forces are friction, aerodynamic drag etc.
So what is the upshot of all this? We have introduced additional concepts of potential energy and conservative forces. The question is: what additional insight or simplification can one obtain using these concepts? This will be subject of the next section.
The essence of this section is to prove the following statement. In an isolated conservative system (i.e., where all the forces that act on the particle can be derived from a potential), the total mechanical energy is conserved. The total mechanical energy of the system is the sum of its potential and kinetic energies. We will prove this statement in what follows. Note the term ``isolated'' - we have not defined this term yet.
Consider, then a particle on which the net force that is acting is . This force may be caused by various
effects including those that are derivable from a potential. Let denote the contribution to the total force
that can be derived from a potential such that 
. The system of interest will now include
the particle and the agency that causes the force due to the potential. The remaining
force will be called the external force which acts on the system and will be called 
. Thus we have that 
. Now consider a system
going from a configuration A to a configuration B. We can compute the work
done in this process by the net force .
But by the work energy theorem proved in the previous section this quantity must be equal to the change in kinetic energy between the points A and B and thus
After some rearrangement, we get that
Defining the total energy of the system in any configuration as E = V + T, we get that,
Thus we reach a powerful conclusion that the work done by external force is equal to the change in the total energy. We shall call this the generalized work-energy theorem.
An isolated system is one which is not under the action of any external force,
i.e., is equal to zero.
Thus we see that in an isolated mechanical system, 
, or that in the process on changing the
configuration from A to B the mechanical energy is conserved! This is an
extremely powerful statement, as will be seen in the examples that follow.
The application of the principle of conservation of mechanical energy will involve a few additional steps. The steps are
A ball of mass m is dropped from a height h. Find the speed of the ball just before it hits the ground.
and the
coordinate of the point B is 
.
. 
.
. i.e., 
as we have seen before. Note the great
simplicity afforded by the generalized work-energy theorem in this example! Assuming the profile of a roller-coaster to be 
, compute the velocity of the roller
coaster at x = L/2 . The mass of the roller coaster may be taken to be m,
and the track to be frictionless. The roller coaster is released from rest at x =
0.01L.
of the track on the roller-coaster. The potential energy function is V(y)=mgy.
The coordinates of the start and end points may also be easily identified.
. , or 
. A ball of mass m is attached a spring of stiffness k. The spring is unstretched when the mass is at the point A as shown. If the mass is released from A, compute magnitude of the maximum deflection in the spring.
. There are no external forces. The coordinate of the point A is 
and that of B is 
where a is the
magnitude of the maximum deflection in the spring (to be determined). 
. , from which we can compute 
.