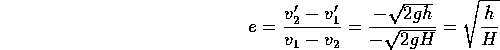EN4 : Dynamics and Vibrations
In the previous chapter, we investigated what happens when we integrate a force through a distance and introduced the concept of work. We were then able to show that the work done by the net force was equal to the change in the kinetic energy of the particle. In addition, we were able to show that the work done by external forces was equal to the change the total energy of the particle. We then inferred that in an isolated conservative mechanical system, the total mechanical energy is conserved.
In this chapter we will take a different strategy, in that we will integrate forces with respect to time. This will give us a new concept called ``impulse''. Just as we had defined kinetic energy, we will define a new quantity called momentum which will depend on the mass and velocity of the body. We will then see that impulse on a particle will be the change in momentum, just as work was equal to change in kinetic energy. We will also arrive at a very important result that if there are no forces acting on a particle, its momentum will be conserved.
Let 
be the net force
that is acting on a particle. Note that the force is assumed to be a function of time. The
impulse of a force in a time interval 
to 
is
defined as the time integral of the force
Note that impulse, unlike work, is a vector quantity. The SI units for impulse is Newton times seconds or Ns.
The linear momentum 
of a particle of mass m with velocity is 
is defined as
Note that this is a vector quantity, and has SI units of kilograms times meters per sec, or kgm/s.
As usual, the first question that comes to mind is ``so what?''. Well, we did not define these quantities in futility. These quantities are related via a relation just as work and kinetic energy were related. To see this, lets take a closer look at Newton's Law. We know that the force applied produces an acceleration, or,
In other words we can restate Newton's Law as ``The rate of change of momentum of a
particle is the applied force''. This is a more general statement of Newton's Law and is
more useful than the old 
. To see this think of a system in which the mass is changing, such as a rocket. We shall,
however, not deal with systems such as this but remain focussed on systems where the mass
is constant.
Having restated Newton's Law in this manner, we are now in a position to derive the
relationship between impulse and momentum. Let us integrate the new form of Newton's Law
from time to . We get
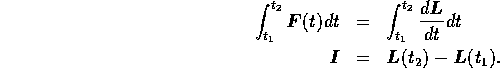
Thus we get a rather interesting result (that looks very similar to the work energy theorem): impulse is equal to the change in momentum.
Note also that when there is no force acting on the particle, its momentum is conserved.
Let us look at some examples that will help gel our ideas about impulse and momentum.
Example 1: A force acts on a particle of mass m initially at rest for a
time interval T, during which it is has a functional form 
. Compute the velocity of the ball at t
= T. The impulse 
. Thus 
or, the velocity
at time T is 
.
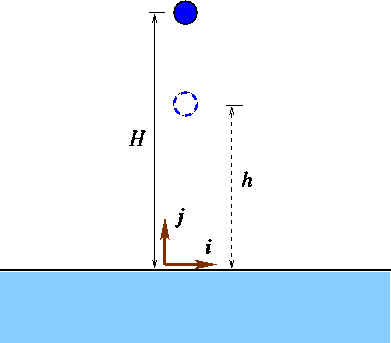
Example 2: A ball is dropped from a height H. After it bounces off the
floor, the ball rises back to height h. Compute the impulse exerted by the floor on
the ball. Let be the
instant at the the ball first makes contact with the ground. At this instant the velocity
vector of the ball is given by 
which implies that the momentum at this instant is 
. Now, let be the time instant at which the ball just
leaves the floor. The velocity vector of the ball at this instant is 
(How?). The momentum at the instant is therefore 
. Now by impulse-momentum
relationship, we have that
Thus the impulse in this case is
So far we have considered only one-particle problems in this course. In the remainder of this lecture we will look at two particles moving in a straight line - what happens when they collide, etc.
Consider two masses 
and 
moving along a
straight line such that they have velocities 
and 
respectively. Assuming that both 
and 
are positive (i.e.,) they are both moving
from left to right, and that 
, we see that the mass will eventually collide with mass . When they collide they apply some forces
on each other and separate after some time. Let us say they have final velocities 
and 
respectively. Our task will be to determine
these two quantities. Let us see how we can apply all that we have learned so far in this
course to determine the answer to this problem.
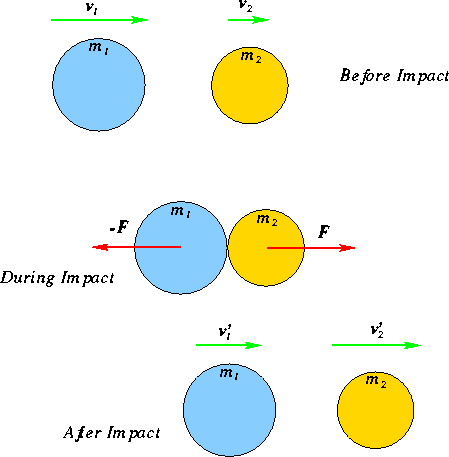
Let us assume that the bodies come in contact at time and remain in contact until some later time . During this time interval
the mass applies a
force on mass . By Newton's third law, the
mass must exert an
equal but opposite force on the mass . We know from the impulse-momentum relation for mass that
Impulse momentum relation for mass gives
From these two relations, we get that
This give us a very powerful statement: The total momentum of the system of two
particles is conserved in collisions!. Taking the required components along the 
-direction, we get
But alas, this gives us only one equation for the two unknowns 
and 
. Thus application of the fundamental
principles that we have learned so far gives us insufficient information to solve this
problem.
This is the first time in we are encountering such a problem. So far when we talked, say about dropping a ball of mass m we did not have to say if the ball was made of steel or wood or plastic. In the case of impacts this is not the case! We cannot solve the problem without the knowledge of some material property. This material property is called the coefficient of restitution. This is defined as
or said in words, it is the ratio of the magnitude of relative velocity after impact (relative velocity of separation) to the value before impact (relative velocity of approach). This quantity depends on the materials that the balls are made of. It is always between 0 and 1. Typical numbers are 0.8 for glass/glass, 0.6 for steel/steel, very close to zero for clay on clay. What is the physical origin of the coefficient of restitution? When this collide they deform. In the deformation process some of the kinetic energy of the balls is converted to other forms of energy such as heat and elastic energy.
Let us look at the limiting cases. When e is unity, we say that the collision is perfectly elastic. In such cases there is no loss of kinetic energy. When e is zero we say that the collision is perfectly plastic. In this case the bodies stick together after collision.
Let us look at some examples:
Example 1: A ball of mass m traveling with a velocity 
collides with an identical ball which is at
rest. If the coefficient of restitution is e, compute the final velocities of the two
balls.
From the principle of conservation of momentum we know that
We also know that the coefficient of restitution is e, and thus
Solving for and , we get that
In the case where e = 1, the mass comes to rest and the mass move with the velocity . When e=0, the mass and stick together and move with the velocity 
.
Example 2: A ball of mass m is dropped on a cement floor from a height H. If the ball bounces back to a height h, compute the coefficient of restitution e between the ball and the cement floor.
We know from Example 2 of Section 4.3 that the velocity of the ball (take this as `` '') just before impact is 
and just after impact is 
. Noting that the velocity
of earth (or the cement floor), which is `` '' in this problem, before and after impact
is zero, we get that
