EN4 : Dynamics and Vibrations
In the last section we discussed impacts that took place when the two particles in question were moving along the same straight line. Such an impact is called direct central impact, and in this case the problem can be completely solved by considering it in a one-dimensional setting. In this section, we shall generalize this to include impact that occurs when the particles are not moving along the same straight line. We shall, however, assume that the particles are still confined to the same plane. Such impacts are called oblique central impacts. We shall make another assumption that the during impact, i.e., when the particles are in contact, there are no frictional effects. This is, of course, an unrealistic assumption but it simplifies our calculations.
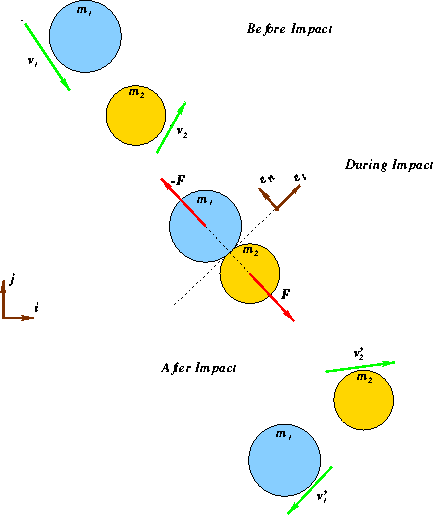
Consider, then, two particles (assumed spherical) of mass 
and 
approaching each other with velocities 
and 
as shown in the figure. The global 
and 
axis are also shown. The question in oblique
central impact problems, like that in the direct central impact problems, is to determine
the velocities 
and 
after impact.
We shall use the impulse-momentum relationship to look at this problem just as in the
case of direct central impact. During the time that the spheres are in contact, they
assert equal and opposite forces on each other. The direction of this force is along the
line joining the centers of the spheres, in other words in the direction normal to the
contacting surfaces. We denote this direction with the unit vector 
; and the tangential direction by 
. As you will see, working
this problem out in this new basis defined by and will be much easier. Using the
impulse-momentum relationship one can easily show that the total momentum of the system is
conserved, i.e.,
Writing components in the basis and we
get that
which is just a mathematical way of stating that total momentum in the normal and
tangential direction is conserved. How many unknowns are there in this problem? If you
look at the equations carefully, you will see that there are four(4) unknowns; they are 
and 
. The principle of conservation of momentum
gives us two equations. We need two additional equations for a complete solution. We may,
of course, bring into action the idea of the coefficient of restitution, which is the
ratio of the magnitude of the relative velocity of separation to that of the relative
velocity of approach in the normal direction, in symbols it reads
Ok, that gives us one more equation making the total number of equations so far three. We need one more equation to solve for the four unknowns. Where do we get this from? Here is where we assume that there is no friction between the spheres, i.e., there is no tangential force on the spheres. Well, then we know from the restated-Newton's Law that tangential component of the momentum of each ball is conserved. But that will give us two equations,
But now we have five equations! Not really, since the last two equations that we just derived would automatically imply that the total momentum in the tangential direction is conserved. Thus we drop the second equation of obtained from the conservation of the total momentum. Collecting all the equations, we get
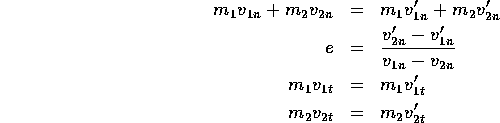
which is a well-posed linear algebraic system for four unknowns. What we shall do now is to apply these equations some oblique central impact problems through some examples.
Example 1: A ball of mass m moving with speed v bounces on a floor
at an angle 
. If the
coefficient of restitution is e, find the angle 
at which the ball emerges from the floor.
Let us assume that the ball is the mass `` '' and that the earth is mass `` ''. In this case the and are parallel to and
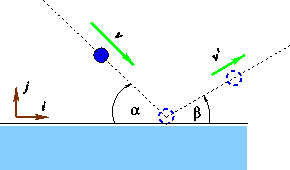
. Thus we can write
the initial velocity of the ball as 
. The velocity of the ball after impact can be written as 
. We know that the velocity
of earth is unaffected in our frame before and after impact. Now, from the third equation
that we had collected before, we have
From the definition of the coefficient of restitution, we get
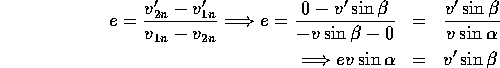
It therefore follows that
Note that the maximum value of is and
this occurs when e = 1. The minimum value of is zero, and this happens when e =
0.
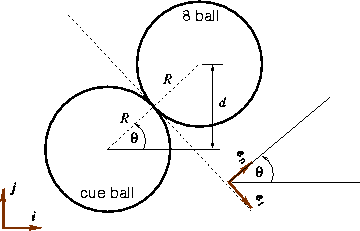
Example 2: A pool player has to decide the distance d at which the cue ball is to placed so that the 8-ball is potted. Both the balls have equal mass m and radius R. Neglect friction.
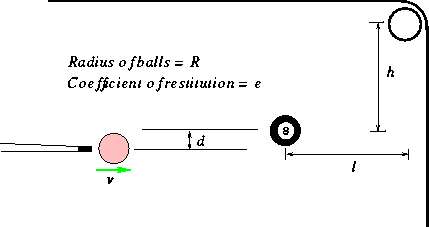
It is clear that for the 8-ball to be potted, its velocity vector has to be inclined at
an angle 
. Our task
will be to determine d such that this happens. To analyze this. construct a
coordinate system with
and as shown. It is
clear that the angle of inclination of with the
direction is 
. Thus in
this coordinate system we can write the initial velocity of the cue ball (mass `` '') as 
. The velocity of the 8-ball is 
. The final velocities may
be written as 
and 
. Let us obtain all
unknowns. From conservation of total momentum we know that
The definition of coefficient of restitution gives us
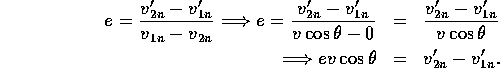
From the conservation of tangential component of momentum of each of the balls we get that
From the first two equations it follows that
Thus the final velocity of the 8-ball is
i.e., it is exactly along . But we know that is inclined at an angle 
to the
axis, and this must be equal to . Thus, imposing that 
gives
This section will define ``rotational'' analogs to linear momentum and linear impulse called ``angular momentum'' and ``angular impulse''. If you have not seen these before they might appear rather strange! You should not find this surprising - these concepts are indeed hard to grasp and to explain! With that warning, lets get to the definitions of angular momentum.
Consider a particle of mass m moving with a velocity 
and whose position vector 
is measured from a point O
with respect to a fixed basis. The angular momentum of the particle about the point O
is defined as
Thus angular momentum is defined as the cross product of the position vector with linear momentum. Several features may be noted:
where is the angle between the and 
. Its direction is normal to the plane
containing and , and is determined by the
right hand rule.
/s. What is the significance of angular momentum? To see this consider a particle of mass m
executing uniform circular motion with angular velocity 
along a circle of radius r. The
velocity at any instant of time is given by 
and the position vector is given by 
. The angular momentum of
the particle about the origin is given by 
. This is amazing! Note that the angular
momentum about the origin is a constant for uniform circular motion just as
linear momentum was constant for uniform straight line motion!
Now we pop the all important question: for linear motion we can state Newton's Law as ``the rate of change of momentum is equal to the applied force'' - is there an analogue for angular momentum? In other words is there an ``Angular Newton's Law''. Lets see. To this end, compute the time derivative of angular momentum
Note that the 
vanishes because velocity is parallel to linear momentum. Amazing! We find a very
interesting result that the rate of change of angular momentum is the applied moment which
is the ``angular Newton's Law'' that we were after. And again, playing the same game, we
see that if the moment of the force acting on a particle about a point is zero, then
the angular momentum of the particle about that point is conserved. You will see
through examples later that this is an extremely useful result.
Using ``Angular Newton's Law'' we can now develop the angular impulse-angular momentum
relationship. To this end, we define the angular impulse 
(about point O) as
By integrating ``Angular Newton's Law'' we come to an analogous conclusion that
Example 1: A ball of mass attached to a string undergoes uniform circular motion at speed v
along a circle of radius r. A second ball of mass is located along the circular path. The mass
collides with mass . The two particles stick
together after collision. Compute the final speed of circular motion.
The initial angular momentum of particle 1 about the point O is
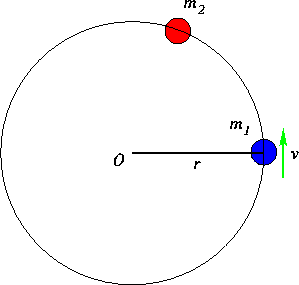
The angular momentum of the particle 2 before impact is
After impact the particles stick together and therefore the angular momenta are
The total angular momentum is conserved, thus
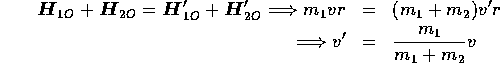
Example 2: Problem 3, Midsemster Exam I (conducted on Tuesday, March 9, 1999).
This example will concern part 3.4 of the question where the angular speed of the
Habitat/rocket stage system is to be determined as a function of time if the length of the
cable as a function of time is 
. Note that from the free body diagram that you obtained in part 3.1,
that the net force acting on both the Habitat and the rocket stage only the tension in the
cable. But this does not produce a moment about the point O, and thus the angular
momentum of the system is conserved. Let us compute the total angular momentum of the
system any given time:
But by conservation of angular momentum this quantity must be equal to to the angular momentum at time t=0 or
whence it follows that
The simplicity afforded by the principle of conservation of angular momentum in solving this problem is indeed impressive!