EN4 : Dynamics and Vibrations

4.8 System of Particles

So far we have looked at systems that contain at most two particles. In this section we shall look into treating systems with arbitrary number of particles. In the process we shall systematically generalize all the theorems that we had derived for a single particle to a system of particles. Before we do this, we shall introduce the concept of center of mass.

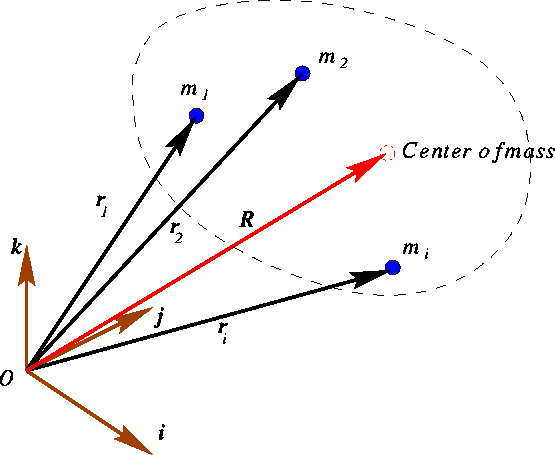
Consider a system of N particles. Each particle will be indexed by a label such as i or j. Thus will be the mass of the particle, and its position with respect to some pre-chosen coordinate system and origin O. The total mass of the system of particles is

We define the center of mass of the system as

The center of mass of the system is a weighted average of the positions of all the particles. Physically you may think of this point as the location of an equivalent point particle of mass M. You may then ask ``what is the velocity of the center of mass?'' Lets see. The velocity of the center of mass, i.e., the time derivative of , is

And similarly the acceleration of the center of mass is

Ok, can we now write Newton's Law for the system? The answer is yes, but we will have to work a bit for it. We will derive this using Newtons's Law for each particle. Say we do this for the particle. We have

Well, lets look at the force carefully. It is the net force acting on the particle i. What causes this force? There are two contributions to the force, one is from an external agency which

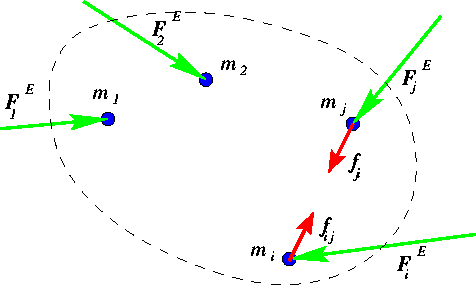
we shall call . Then there is a force that the particle experiences due to interactions with all other particles and this gives rise to an internal force on the particle which we shall denote by . Note that this can be written as

where is the force exerted by particle j on the particle i. Assuming that these forces between particles are equal and opposite, i.e., assuming that these forces obey Newton's third law, we get

We are all set to derive the Newton's Law for the system of particles. Sum the right hand sides and left hand sides of the Newton's Law for individual particles:

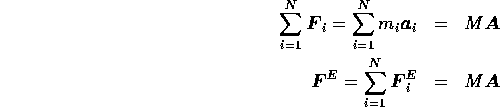
Thus Newton's Law for the system of particles reads as ``The sum total of all external forces is equal to the total mass of the system multiplied by the acceleration of the center of mass''.

Recall that we had restated Newton's Law in terms of momentum. Is it possible to do the same in the case of a system of particles. Note that this is possible by a simple manipulation. For

where is the total linear momentum of the system. Well, we then have that

In words we have ``The rate of change of the total momentum of the system is equal to the net external force''. From this we can derive an extremely powerful conservation law. If the sum of all the external forces that act on the system vanishes, then the total linear momentum of the system is conserved! We had seen this in the case impact of two balls, but it is actually true for a system with arbitrary number of particles.

Let us turn now to work and energy relationship for a system of particles. To do this we shall have to write the total energy of the system. The kinetic energy of the system is simply the sum of the the kinetic energies of individual particles, or,

What about the potential energy? Well, it depends on if the force acting between particles, i.e., the internal force, are conservative. If it is so, we can put down a potential energy function which depends on the position of all the particles, as . As an example, if the interaction between particles arises from gravity, we have

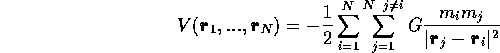
The total of the system is

Now the generalized work energy theorem in this case will give us that the total work done by external forces is equal to the change in the total energy of the system, or

Using this relation, we come to the conclusion that if the particles experience no external forces, then the total energy of the system is conserved.

And finally we turn to angular momentum. As you might have expected, the story here is somewhat more tricky. What sort of an law do we expect? We might guess

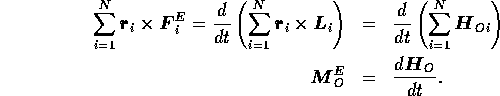
This turns out to be true, but not without an additional assumption that the internal forces that act on the particles are directed along the lines joining them. Put in an equation, it means that

Try to prove this yourself.

Example 1: A man of mass M standing on a ski board shoots at a deer. If the bullet of mass m leaves the gun at a speed v (with respect to the ground), find the velocity of the man. The frictional force between the man and the ground in negligible.

Let us fix a coordinate system such that the bullet moves horizontally along the direction. Since there are no external forces acting on the system containing the man and the bullet, the total momentum must be conserved. But the initial momentum of the system is zero, and thus

Thus V is - m v/M.

Example 2: Problem 4/2, Meriam and Kraige.

Set up a coordinate system such that the direction points upwards. Using this coordinate system, the net external force on the system can be written as

Where P is the tension in the rope at D. Note that we need not consider the tensions in the rope between A and B, and C and D since they can be thought of as internal forces acting between the monkeys. The total external force acting on the system must be equal to the total mass times the acceleration of the center of mass. In our case

Applying Newton's Law for systems, we get

from which we obtain that

Noting that m/s , , m/s , we get P = 187.2N.

Example 3: A chain of length is placed on a table such that a very small portion of the chain hangs over the end of the table. Assuming that there is no friction, compute the speed of the chain just when it has completely left the table.

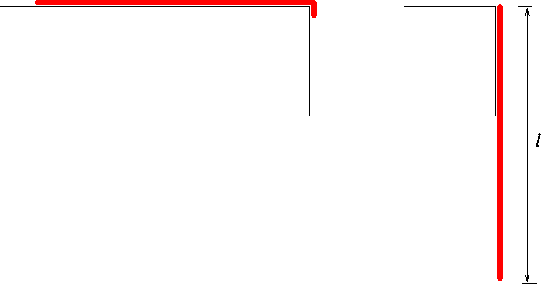
Since there is no frictional force acting on the chain, this is a conservative system and therefore energy is conserved. Let us fix a coordinate system such that the table is at y=0. Let A be a configuration when the chain is on the table. The potential energy in this configuration is , and so is the kinetic energy, i.e., . In the configuration B, the chain has just left the table. The potential energy of the system in this configuration is , since the center of mass has moved down by a distance . The total energy of the system in this configuration is . Since we get that .