EN4: Dynamics and Vibrations

Division of Engineering
Brown University

Examples of straight line motion problems

Review: Straight Line Motion with Constant Acceleration.

A particle is at position and has speed at time t=0. If the particle accelerates at a constant rate , find expressions for the speed and position of the particle as functions of time.

Start by integrating the acceleration to find the velocity

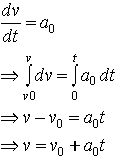
Now integrate the velocity to find the position

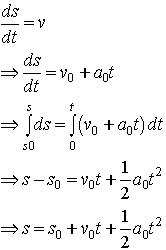
You will probably remember these results from your carefree youth… You can use the results as formulae for any problem where the acceleration is constant. In general, however, you will have to do the calculus from scratch.

Example 1: An accelerometer is attached to a structure to measure its vibration characteristics. The structure is set in motion by releasing it from rest at an initial position =3cm. The resulting acceleration may be approximated by , where A= and rad/sec. Find expressions for the velocity and position of the structure as a function of time.

As always we integrate the acceleration to get the velocity and then integrate the velocity to get the position

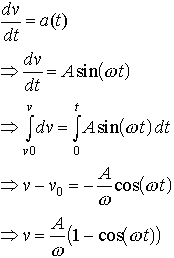
where we have noted that because the system was released from rest.

Now do the calculus again to get the position

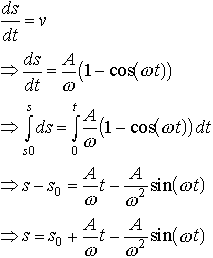
We can now substitute numerical values to see that

Example 2. In many problems, you will need to calculate the position and velocity of an object as a function of time, and then use the results to answer some problem. Here is an example. Suppose you want to throw some keys to a friend standing on a second floor balcony. If you release the keys at m above the ground, what initial vertical velocity is needed for them to reach your friend’s hand a height h=6m above the ground?

We clearly will need to be able to calculate the position of the keys as a function of time to be able to answer this problem, so that’s where we start. We first need to get the acceleration of the keys: draw a free body diagram showing the force acting on the keys

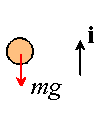
Hence, Newton II shows that

so that a=-g.

This is therefore a case of constant acceleration. We can merely write down the position and velocity from the results we calculated earlier:

Now let’s review the data we are given. We know that the keys are released from . This leaves us with 4 more unknown quantities in our equations: s,t,v,and . We need to find some physical conditions that will give us these values.

Two observations:

(i) If you throw something vertically up in the air, it slows down, comes to a stop at its maximum height, and falls back down again;

(ii) If you throw the keys too fast, they will go higher than 6m; if you throw them too slowly, they will not reach 6m.

Thus, the critical vertical velocity is such that when the keys come to a stop, they just reach 6m.

Suppose the keys reach their maximum height at a time . Since the velocity is zero at this time, we have

We need to find such that s=6m at time . Thus

Example 3: An aircraft carrier of mass M is traveling with speed when its engines are shut down. Find an expression that may be used to determine how far the carrier will travel and how long it will take to stop.

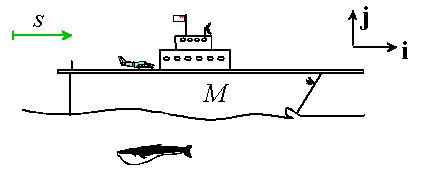
First, describe the problem. Idealize the ship as a particle, let s denote the distance traveled after engine shutdown, and let v denote the ship’s speed.

We will assume that the carrier is slowed by hydrodynamic drag. As a first approximation, we will assume that the drag force may be expressed as

where v is the speed of the ship and is a constant.

As always, we start with a free body diagram showing the forces acting on the ship. There are three forces: weight, buoyancy and drag

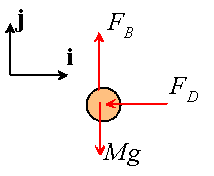
The acceleration of the ship may be written in terms of either its speed or distance traveled as

Write down Newton’s second law

so, comparing I and j coefficients we learn that

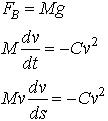
Now we can do some calculus. The second equation will give us an expression for velocity as a function of time, as follows

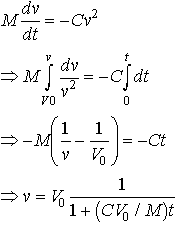
We could integrate this to find the position of the ship as a function of time. Recall that v=ds/dt, so

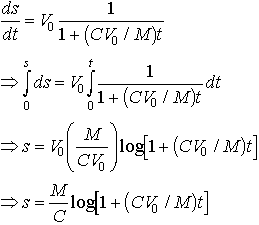
The third equation will give us an expression for the speed of the carrier as a function of its distance traveled

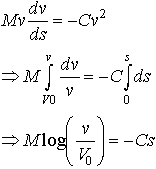
Now, let’s see what the math is telling us. We have an expression for velocity as a function of time

so we can try to find the time at which v=0, but the answer is ! This is not good.

Let’s see if we can do better finding the distance required to stop. We have that

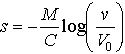
and again, when v=0, . Bummer…

What has gone wrong here? Well, we should ask three questions:

(i) Is the answer physically reasonable? Not really: we wouldn’t expect a ship to go on traveling indefinitely (a possible exception is the `Flying Dutchman,’ a famous ghost ship…)

(ii) Did we do the math right? A good way to check is to look at the physical dimensions of all our equations. Everything seems to check out.

(iii) Did we make any incorrect assumptions? Well, what assumptions did we make. First, we idealized the tanker as a particle. That may be a stretch, but the tanker doesn’t deform or rotate significantly while it’s slowing down so this approximation should be OK. We assumed that Newton’s laws will work. That’s probably true as well. We also assumed that drag force is proportional to the square of the velocity. This is the assumption that is most likely to be incorrect.

Indeed, it turns out that is valid only for high velocities, when the drag force is primarily associated with the inertia of the fluid – as the ship pushes through the water, it must exert a force on the fluid to move it aside. An equal and opposite force acts on the ship. At lower velocities, the accelerations in the fluid are much smaller so the hydrodynamic drag force is less significant. Instead, the ship’s motion is resisted by viscous drag in the water. Viscous drag is caused by the (rather weak) attractive forces that act between water molecules. It varies linearly with velocity

You can verify for yourself that with viscous drag only, the speed and distance traveled by the ship are given as functions of time by

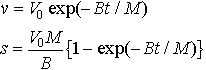
while the distance traveled is related to the speed by

Now, the ship still takes an infinite time to stop, but the total distance traveled is finite and is given by

Finally, we could combine our results to estimate the total distance traveled by the ship. To do this, we could split the motion into two parts. If the hydrodynamic force is greater than viscous drag, we will assume that motion is resisted by hydrodynamic drag only. If the viscous drag is greater, we will assume that motion is resisted by viscous drag only.

The velocity at which the two drag forces are equal is given by

Assuming that , the distance required to slow from initial speed to speed under hydrodynamic drag is given by

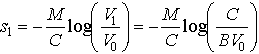
The additional distance required to slow from speed to zero under viscous drag is

so the total distance to stop is

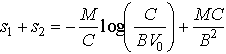
The time required to stop is still infinite.

Let’s substitute some numbers to get an estimate. Specifications for aircraft carriers are easy to find on the web. For example, for the Nimitz class:

Length: 317m (1040 feet – that’s a mighty short runway to land a jet on!)

Beam (that’s width to landlubbers): 40.8m (134 feet)

Displacement (that’s mass ): 87,998 metric tons (a ton is 1000 kg)
Speed: 30 knots (that’s sea miles per hour, or 55km/hr or 15 m/s)

It’s harder to estimate the constants C and B. There are a few computer simulations of hull drag published on the web. Expressions for drag force are normally expressed in the form

where is the density of the fluid, A is the immersed area of the hull, and is the drag coefficient – a number which is either computed or measured for a particular hull. The drag coefficient appears to be a number around according to simulations.

Our constant C therefore follows as

The density of sea water is of the order of 1000 , and we can estimate the immersed area by approximating the hull as a rectangle length L, width W and height H, and using the fact that the weight of water displaced by the hull must be equal to the weight of the ship (Archimedes principle) Thus

This gives . A draft of about 20 feet seems about right.

The immersed area is then

Therefore 9000 is a reasonable number for C.

The number B is even harder to find, because viscous drag kicks in at such low velocities that it is of little consequence to ship design. We’ll make a wild guess and say that viscous drag kicks in at about 1 knot (0.5m/s). This gives

Luckily our estimate turns out not to be particularly sensitive to the value used for B.

Finally, plug all our estimated numbers into the expression we calculated for the stopping distance to conclude that the stopping distance is around 30km – that’s about 20 miles!

Controlling the drag forces acting on a ship is a matter of considerable practical importance. The drag forces are actually rather more complex than the simple forms we’ve used here – there are several different contributions to drag, including skin friction drag (the viscous term), form drag (primarily due to the inertia of the fluid) and wave drag (a large ship pushes a big wave of water along with it – lifting the water in this wave contributes to drag and is very significant at high velocities). There’s an interesting non-technical article on the subject in Scientific American.

Example 5: A spring-mass oscillator consists of a mass and a spring connected as shown. The coordinate s measures the displacement of the mass relative to its position when the spring is unstretched. If the spring is linear, the mass is subjected to a deceleration proportional to s. Suppose that and that you give the mass a velocity v=1 m/s in the position s=0.

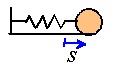
(a) How far will the mass move to the right before the spring brings it to a stop?

To answer this, we need an expression for distance moved as a function of velocity. We can get one by integrating the alternative expression for acceleration:

We are given that the initial velocity and the initial position . Consequently, when the mass stops (v=0), we have

.

Why do we get two solutions? Well, the mass vibrates back and forth: first it moves 1m to the right (s=+1/2m) and then 1m to the left (s=-1/2m). Consequently, there are two positions where v=0. We are told to find how far the mass moves to the right, which is

.

(b) What will be the velocity of the mass when it has returned to the position s=0?

We already know the relationship between s and v from the preceding part of the question:

We can simply set in the result to see that

Not enough information is given in the question to decide whether the velocity is positive or negative. The first time the mass returns to s=0, the velocity is negative, the second time it is positive, and so on.

Although we are not asked to do so in the question, we may calculate s as a function of time. We have that

The velocity and acceleration follow as

Observe that a=-4s, as required.

Comment

We now have all the techniques we need to compute position and velocity from acceleration, at least for the case of straight line motion. One final remark is in order. The procedure we described here only works if we are given , or , that is, acceleration is either: (i) only a function of time; (ii) only a function of velocity or (iii) only a function of position.

It sometimes happens that acceleration is a function of all three! For example, when we analyze forced vibrations of a spring-mass-damper system later in the course, we will find that the equation for acceleration is

Here, , , and are constants.

The good news is that this equation can be solved. The bad news is that the solution is much more difficult than the problems we’ve discussed here – the worst news is that you will have to learn how to solve it.