Engineering 3A: Introduction to Engineering

Problem Set 5

Due Thursday, October 28, 2004

You can use Maple on any problem of this assignment, but hand in a copy of your Maple worksheet if you do.

 

1. In this problem you will estimate reactions at the base of the Washington Monument during a crosswind. The windspeed v varies linearly with altitude y, so that v(y)=v_my/h where h is the height of the tower at the base of the pyramidion (that’s what they call the pointy part on top).  The wind speed at altitude h is v­_m.

The force  per unit length of the tower due to the wind is given by

,

where d(y) is the width of the tower at elevation y,  r is the mass density of air, and C_D is the drag coefficient; C_D=1.5 for a square cross section. The mass of the tower is m_T.

 

a. Derive an expression for the horizontal force distribution f_D(y) in terms of  r, C_D, a, b, h, and v_m. You can neglect the wind force acting on the pyramidion in this problem.  3 points

 

b. Draw a free body diagram showing all forces acting on the monument. 3 points

 

c. Calculate the reaction forces and moment at the base of the pyramid.  5 points

 

d. Evaluate your answers for a hurricane with wind speed  at the top v_m= 100 meters per second (229 mph) and approximate dimensions for the tower: a=10.5 m, b=16.8 m, h=150 m, m_T=8.2x10⁷ kg.  3 points

 

e. The foundation consists of four deep piles. While these piles can support very large compressive forces, they are at risk of being pulled from their footings if the piles are placed in tension.   The tower supports may be modeled as pinned at the downwind pair of footings and on rollers at the upwind pair. Draw a free body diagram showing all forces acting on the tower. 3 points

 

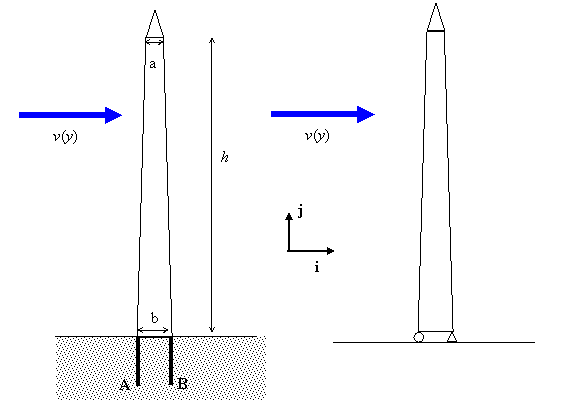
f. Calculate the reactions at the upwind and downwind pairs of supports. Are any of the piles in danger of being pulled from their footings? 3 points

 

g. EXTRA CREDIT: Use the word pyramidion casually in conversation at dinner. Briefly summarize the conversation. 3 points
2. In this problem, you will calculate the normal stress (force per unit area) in the walls of the Washington Monument on a calm day (no wind!). The cross-section of the tower is the hollow square shown below. The hollow inner core has width c (independent of y).  The total mass of the pyramidion is m_p and the mass of the shaft is m_s=m_T-m_p.

 

a. Find the mass density of the shaft in terms of m_S, a, b, c, and h. Evaluate the answer for  the actual dimensions for the tower: a=10.5 m, b=16.8 m, h=150 m,  c=8 m,  m_T=8.2x10⁷ kg, and m_P=3x10⁵ kg. 3 points

 

b.  Calculate the axial force f(y) (in Newtons) carried by the tower walls. Use the sign convention for internal axial forces positive when tensile. See the figure below for help! Plot |f| versus y. 3 points

 

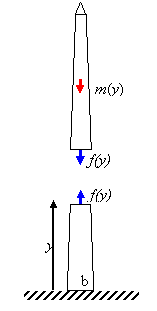
d. Finally, plot the stress (force per unit area) in the tower walls. Compare the maximum stress with the compressive strength of the marble and granite used for the walls of the tower, which  is approximately 100 MPa=10⁸ Newtons per meter squared. 3 points

 

 

3. A flexible, inextensible cable of length L is suspended between two points; one at (0,0) and the other a (x_e,y_e). The weight per unit length is w.  The cable takes on a shape described by  y(x). You will use Excel to calculate the shape of the curve in the second part of this problem, but for now think of this shape as known.

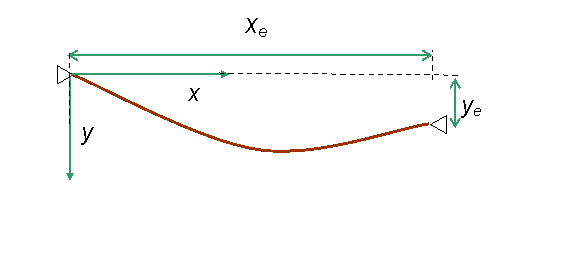
Let T₁ and T_e be the cable tensions at the cable endpoints (0,0) and (x_e,y_e), respectively. A free body diagram showing all forces acting on the cable just below the attachment points is shown below:

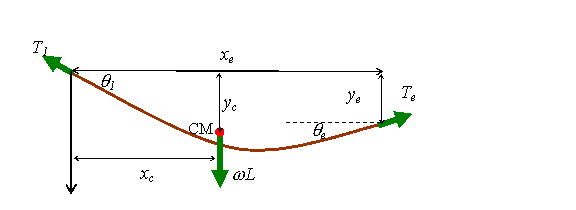
Here, q₁ and q_e are the angles subtended by cable and the horizontal at the endpoints, and x_c is the position of the center of mass for the suspended cable.

 

a. Find expressions for T₁, T_e in terms of w, L, q₁ and q_e. 2 points

 

 

b Find an expression for the horizontal coordinate x_c of the center of mass of the cable in terms of x_e, y_e, and q₁ and q_e. 1 point

 

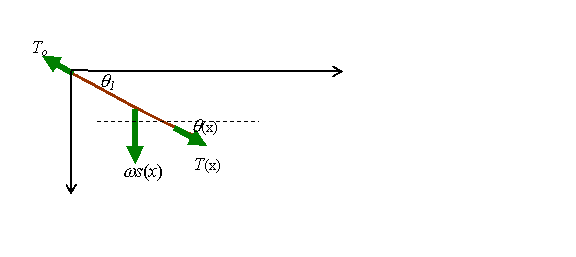
c. A free body diagram showing all forces acting on the section of the cable between the point (0,0) and (x,y(x)) is shown below. Here, s(x) is the length of cable suspended between (0,0) and (x,y(x)). Show that T(x)=T₁cosq₁ /cosq(x). 1 point

d. Use Excel and the principal of minimum potential energy to find the shape of the cable and the tension T(x) along the cable.

 

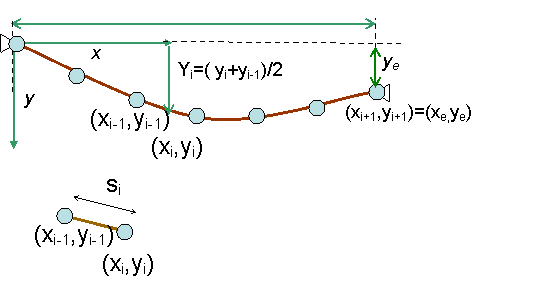
To accomplish the path optimization, divide the cable into N segments as shown. The weight of the i^thsegment is given by w_i=ws_i, where s_i is the segment length. The energy of the i^th segment is  E_i=-w_iY_i=-w_i(y_i+y_i-1)/2. You want to minimize the total potential energy  for the cable, subject to the constraint that

 

 

xe

Have excel calculate the horizontal position x­_c of the center of mass of the hung cable using the answer to part (b). Plot the cable shape and a vertical line at x=x_c showing the horizontal position of the center of mass.

 

Calculate the tension in the first segment using the expression for T₁ arrived at in part a. The tension in subsequent sections can be found using the relation in part c. Plot the cable tension T(x)/(wL) as a function of position x along the cable.

 

Show your results for a cable of length 2 with x_e=1, and each of y_e=0 and y_e=1. 10 points

 

e. The electric transmission cable shown has a weight density of 30 pounds  per foot. It is to be strung over a 600 foot span (x_e=600) and connected to a pole 50 feet below the start point . Cable sag should not exceed 50 feet from the initial point. Determine the minimum cable length required and the tension in the cable. 3 points

 

EXTRA CREDIT AND VALUABLE PRIZES: Program Excel to find the vertical position y_c of the center of mass of the cable, and plot its exact location on the graph. 3 points