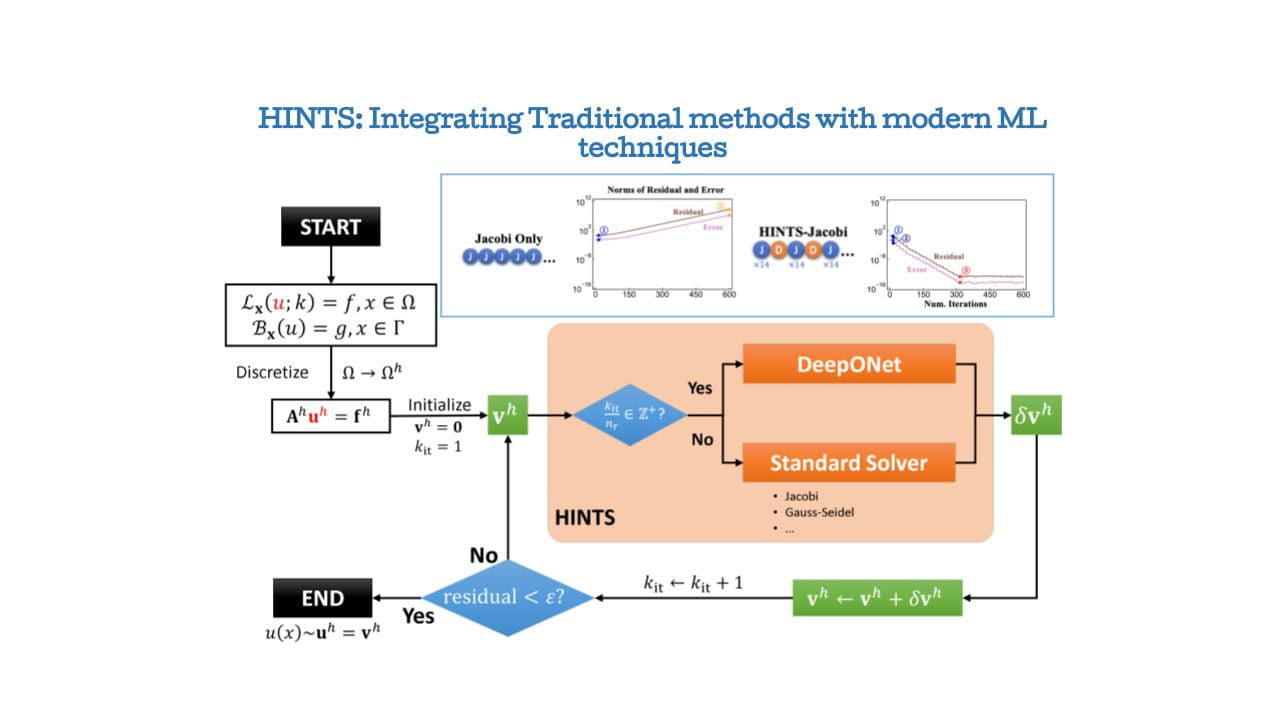
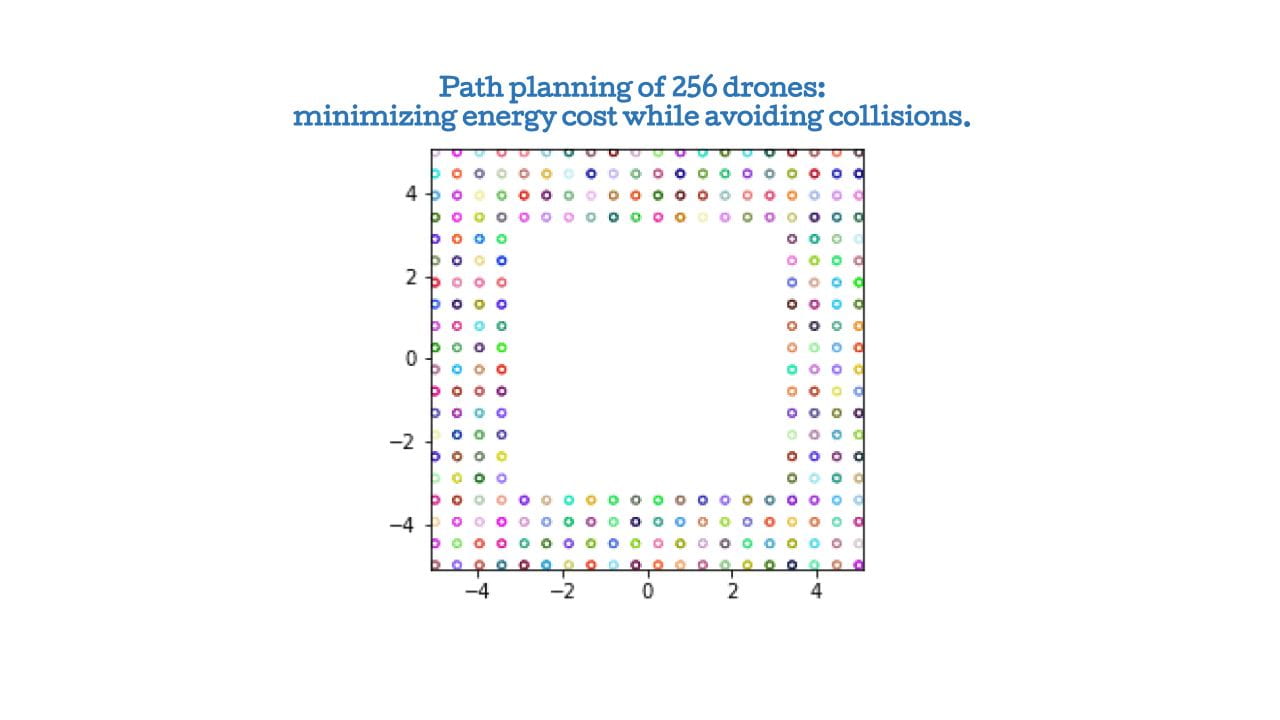
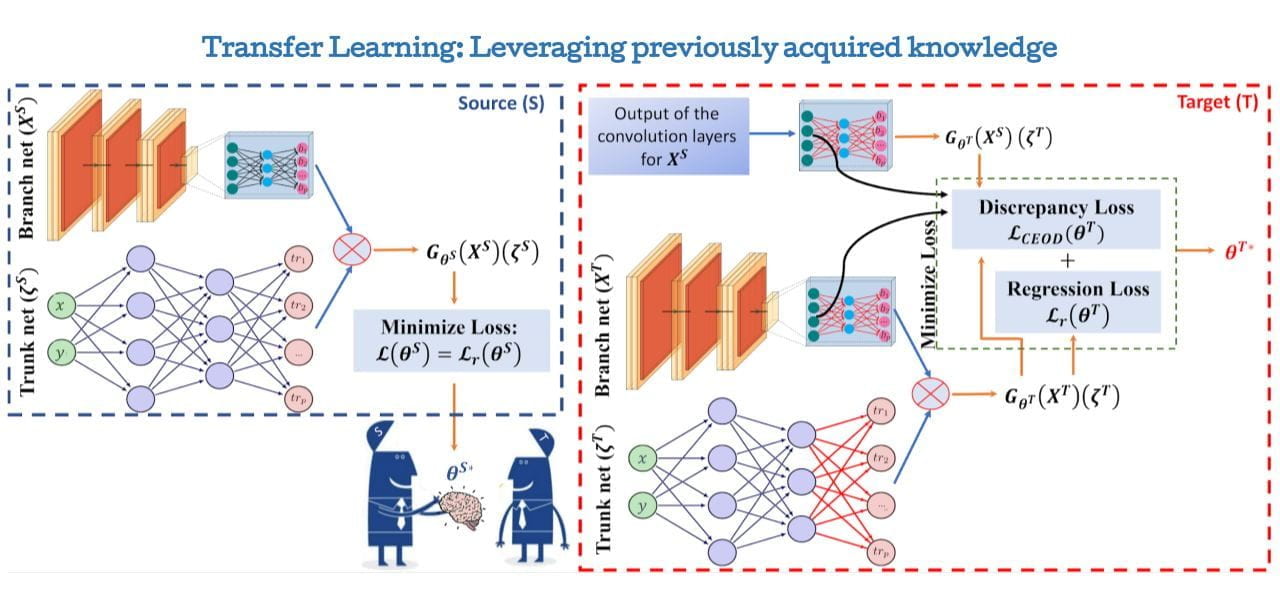
Math + Machine Learning + X: Home of PINNs and Neural Operators

The CRUNCH research group is the home of PINNs and DeepONet – the first original works on neural PDEs and neural operators. The corresponding papers were published in the arxiv in 2017 and 2019, respectively.
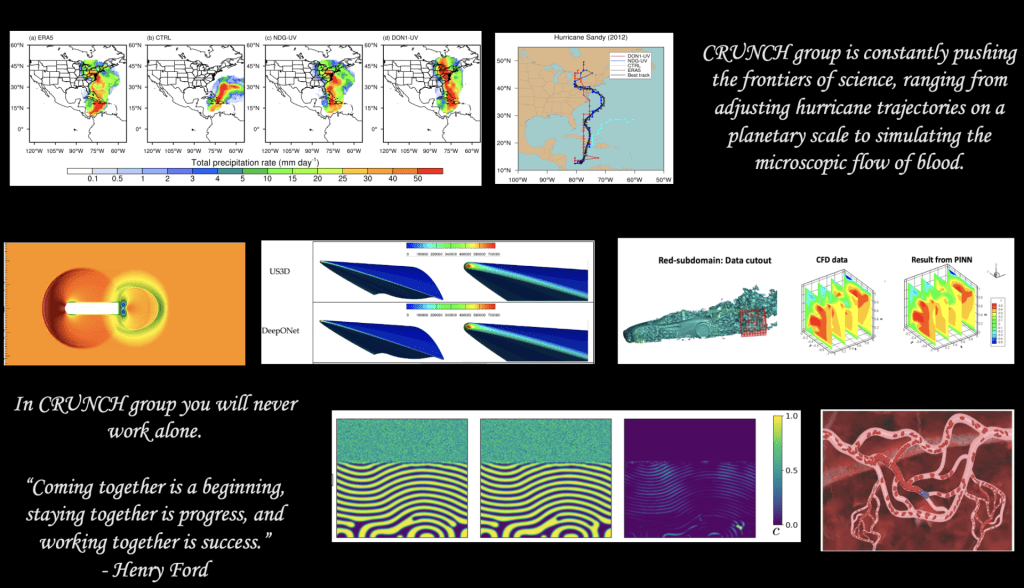
The research team is led by Professor George Em Karniadakis since the early 1990s in the Division of Applied Mathematics at Brown University. CRUNCH members have diverse interdisciplinary backgrounds, and they work at the interface of Computational Mathematics + Machine Learning + X, where X may be problems in biology, geophysics, soft matter, functional materials, physical chemistry, or fluid and solid mechanics.
CRUNCH is supported generously by AFOSR, DOE, ARL, ONR and several industrial partners, including Ansys, Dassault/Simulia, Takeda, Hypercomp, PredictiveIQ. We have joint projects with many USA Universities, including MIT, Stanford, Caltech, University of Utah. We welcome collaborators and visitors from around the world with bold ideas from diverse fields.
CRUNCH supports diversity and inclusion. We have supported the MET School @ PVD, WISE@Brown, and the Association of Women in Mathematics@Brown.