Projects
Project 1: Computing deformation measures from DIC measurements
Digital image correlation is a powerful and comparatively inexpensive technique for measuring deformation fields in materials and structures with micron scale resolution. The basic principle is to take a series pictures of a speckle pattern on a surface during deformation, and to determine displacement fields by matching similar regions in two successive images. An example of displacement contours extracted from DIC measurements on the surface of a tensile specimen of steel [1] is shown in the figure. 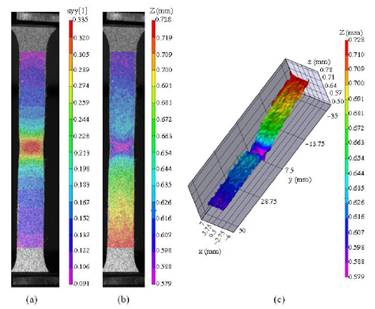
In the example shown, only the surface of the specimen can be observed. In transparent materials, it is also possible to the full 3D displacement field in a specimen. Professor Franck’s lab uses such a system to measure deformation in a soft gel substrate beneath a living cell [2,3]. Your mission in this project is to write a similar MATLAB program.
Your goal will be to read a sequence of images of a deforming specimen, use the MATLAB image processing toolbox to determine the displacement field, and then compute various deformation, strain, and strain rate measures in the gel, and display the results graphically. You can choose what measures you compute, how you compute them, and how you will display the data, and can add whatever bells and whistles you like to your code – it could be just a basic MATLAB script, or a more fancy GUI driven code.
- Jason Coryell, Josh Campbell, Vesna Savic, John Bradley, Sushil Mishra, Shashank Tiwari, Louis Hector, Jr. “Tensile deformation of quenched and partitioned steel - a third generation high strength steel,” Supplemental Proceedings, Vol 2, Materials Properties, Characterization and Modeling, 555-562 2012
- Franck, C., Hong, S., Maskarinec, S.A., Tirrell, D.A., Ravichandran, G., “Three-Dimensional Full-Field Measurements of Large Deformations in Soft Materials using Confocal Microscopy and Digital Volume Correlation,” Experimental Mechanics, 47, 427-438, 2007.
- Jennet Toyjanova, Eyal Bar-Kochva, Christian Frank, personal communication, 2012.
Project 2: Measuring the constitutive behavior of elastomeric sheets
Matlab code to read voltage from arduino
Instructions for wiring the strain gage amplifier

While most of the governing equations in continuum mechanics are invariable physical laws, the constitutive law for the solid or fluid of interest must always be determined and calibrated experimentally. Measuring the response of a material to prescribed loading is thus a standard problem in solid and fluid mechanics.
In this project, you will design and construct a simple apparatus to measure (approximately) the response of a thin elastomeric sheet to uniaxial and biaxial loading. You will use your equipment to select and calibrate a constitutive model that fits your data.
You will need to devise some way to apply prescribed forces to the specimen, and to measure the resulting deformation. Your image processing code from project 1 might be helpful for this purpose.
A few basic materials, hand-tools and supplies will be provided for you to work with. You can use other equipment and materials if you wish, but please acquire them legally… Use of facilities such as JEPIS, rapid prototyping, research engineer/technician help, or outsourcing to developing countries is not allowed!
Some questions you might try to answer include
- Is the material incompressible (or close to it?)
- Is the material isotropic?
- What is its uniaxial and biaxial response?
- Which hyperelastic potential gives the best fit to the measured data? What parameters yield the best fit?
The project may be done individually, or in groups of up to 4 people.
