 EN224: Linear Elasticity
EN224: Linear Elasticity 
Division of Engineering
7.6 Solving Half-Plane Problems Using Analytic Continuation
Some of the most interesting boundary value problems in linear elasticity have been solved using the idea of analytic continuation, which reduces many boundary value problems to a so-called Hilbert problem, with a known solution. Examples include the displacement and traction boundary value problem for the half-plane and the disk; contact problems (both for half-spaces and disks); crack problems (including cracks on the interfaces between dissimilar solids); and problems involving dislocations interacting with boundaries.
The method is quite involved and we will not have time to explore it in full. Instead, we will outline the main ideas behind the procedure, and use it to solve a few representative problems.
The Continuation Theorem
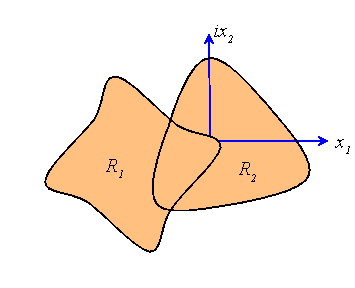
Suppose that ![]() and
and![]() are analytic functions in regions
are analytic functions in regions![]() and
and ![]() .Suppose that the two regions intersect in a domain R
and there exists an infinite sequence
.Suppose that the two regions intersect in a domain R
and there exists an infinite sequence![]() of discrete points in R
with at least one limit point
of discrete points in R
with at least one limit point![]() on which
on which
Then the function
is analytic in the union of![]() and
and![]() . The function is
. The function is
![]() said to be the analytic continuation
said to be the analytic continuation![]() of into
of into![]() ; similarly,
; similarly,![]() is the analytic continuation of
is the analytic continuation of![]() in
in![]() .
.
For our purposes, we will be considering regions that intersect along
a line L, and![]() along L. In this case
along L. In this case ![]() is analytic in
is analytic in![]()
The idea of analytic continuation provides a powerful tool for solving half-plane problems, and can also be used to solve problems involving regions with circular boundaries. We will illustrate the technique by using it to solve half-plane problems here.
The method of stress continuation for a half-plane
For our first problem, we will attempt to determine the fields inside a half-space subjected to a prescribed distribution of traction on its surface, as shown in the picture.
Suppose that the region of interest is the upper half-plane, which we will refer to as R+.
The problem will be solved using analytic continuation.
Here is the basic idea. In the usual formulation, we need to find two
complex potentials,![]()
and ![]() . However, when we solve a half-plane problem, the potentials
in R- (the lower half-plane) are arbitrary – we can choose
the potentials in R- in any way we like, without changing the stress
and displacement fields in R+. This observation allows us to find
an analytic continuation of
. However, when we solve a half-plane problem, the potentials
in R- (the lower half-plane) are arbitrary – we can choose
the potentials in R- in any way we like, without changing the stress
and displacement fields in R+. This observation allows us to find
an analytic continuation of![]() in R- (i.e. we find a function
that is analytic in both R+ and R-), and then using the definition
of
in R- (i.e. we find a function
that is analytic in both R+ and R-), and then using the definition
of![]() in R- to replace
in R- to replace![]() in R+. Then,
instead of having to find two analytic functions in R+, we need
to find one potential
in R+. Then,
instead of having to find two analytic functions in R+, we need
to find one potential![]() that is analytic in both R+ and R-, and
satisfies certain boundary conditions on the real line.
that is analytic in both R+ and R-, and
satisfies certain boundary conditions on the real line.
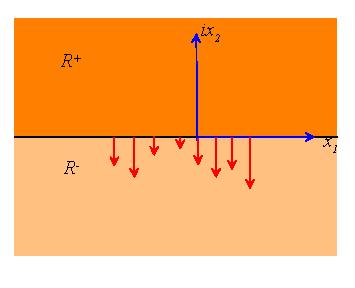
For example, we will show that the following representation will generate
displacement and stress fields in R+ with the surface of the half-space
free of tractions. Let![]() be analytic in both R+ and R-,
and set
be analytic in both R+ and R-,
and set
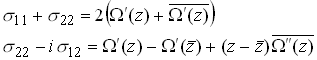
You can check that the surface is free from traction by letting the imaginary part of z approach zero (from above) in the expressions listed above.
The precise way we define![]() in R- is arbitrary. We
usually look for a definition that will make the resulting boundary conditions
as simple as possible. (The procedure we are using here is a bit like the
method we used to solve 3D half-space problems: we tried to superpose a
list of potentials that would simplify the boundary conditions. We had
to use our insight to find the right way to combine the potentials).
in R- is arbitrary. We
usually look for a definition that will make the resulting boundary conditions
as simple as possible. (The procedure we are using here is a bit like the
method we used to solve 3D half-space problems: we tried to superpose a
list of potentials that would simplify the boundary conditions. We had
to use our insight to find the right way to combine the potentials).
There is a systematic approach you can follow to devise an appropriate continuation, however, which we will illustrate for the case of a traction boundary value problem.
We start with our earlier complex variable formulation. Let ![]() be
analytic in R+, and set
be
analytic in R+, and set
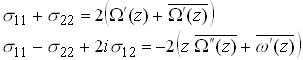
Now, suppose that some region of the real axis is unstressed, i.e.
Where L is a region on the surface.
In terms of the complex potentials
We will introduce the notation
whence
This boundary condition may be re-written in terms of the functions
which are analytic in R- . Note that some books (Muskhelishvili, for example) use the notation
but in my view this is confusing and we won’t use it here.
Now, observe that
Whence, substituting back into the preceding equation and taking complex conjugates:
This condition is equivalent to the statement that the function ![]() '(which
is analytic in R+) has the same value as the function
'(which
is analytic in R+) has the same value as the function ![]() (which
is analytic in R-) on a line segment L. Therefore, by the
continuation theorem, these two functions continue one another analytically
across the line L. We can therefore think of these two functions
as a single complex potential, which is analytic everywhere, and set
(which
is analytic in R-) on a line segment L. Therefore, by the
continuation theorem, these two functions continue one another analytically
across the line L. We can therefore think of these two functions
as a single complex potential, which is analytic everywhere, and set
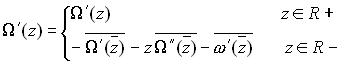
We can integrate these equations to see that
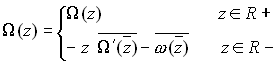
We can use this result to find an expression for![]() in R+:
in R+:
Finally, eliminate ![]() from our expression for displacements
and stresses in R+ to obtain
from our expression for displacements
and stresses in R+ to obtain
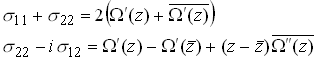
as required.
Exercise: To check that you’ve understood the procedure outlined above, try and see whether you can devise a procedure for generating fields in the upper half-plane with zero displacement on the real line. If you follow the procedure we outlined very closely, you should find the following expression for the displacement field:
Challenge: If you found the preceding exercise trivial,
try to devise a method of analytic continuation for a circular region (either
an infinite solid with a hole, or a disk) with a stress free boundary.
In this case, it is helpful to note that if![]() is analytic in |z|<1,
then
is analytic in |z|<1,
then ![]() is analytic in |z|>1
is analytic in |z|>1
We now have a method for solving problems involving a half-plane with a traction free boundary. In fact, this approach can be extended to solve problems involving arbitrary tractions acting on the surface of the half-plane, as we will see in the next section