
EN4: Dynamics and Vibrations
Division of Engineering
Brown University
2.3 Straight line motion of a particle
In the preceding section, we discussed how to find the acceleration of a particle subjected to a given force. In practice, we are rarely interested in the acceleration of the particle, we would much prefer to compute its position as a function of time.
In this section and the following one, we will show how to compute the velocity and/or position of a particle from its acceleration.
There are two principal reasons you might wish to do this. Firstly, when setting up a model of a mechanical system, you apply Newton’s laws. These will generally give you expressions for the acceleration of each particle in your system as a function of time. You will have to integrate the accelerations to find the velocities.
Secondly, you often measure the acceleration of a system, if you are interested in determining its motion. For example, the most common way to measure vibrations in a structure is to attach an accelerometer to a point of interest. An accelerometer is a small electro-mechanical device that gives you an electric signal proportional to its acceleration. A typical 3 axis accelerometer is shown in the picture below

The accelerometer will give you a signal showing acceleration as a function of time, as shown below
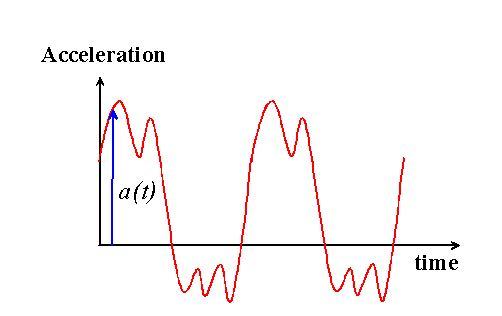
and you will then need to integrate the accelerations to determine the velocity and position of your structure.
Accelerometers also form the heart of inertial navigation systems, which are used in guiding spacecraft and military aircraft (Civilian aircraft use GPS or LORAN, but military aircraft need systems that cannot be jammed). The heart of an inertial navigation system is a platform which is kept in a fixed orientation using gyroscopes. Three accelerometers are attached to the platform to record the accelerations in three mutually perpendicular directions. The signals are integrated to determine the position of the spacecraft as a function of time.
For simplicity, we will begin by assuming that the particle moves along a straight line. We will see shortly that a particle travels in a straight line if
(i) The resultant force on the particle always acts in the same direction and
(ii) The initial velocity of the particle is zero, or is parallel to the direction of the resultant force.
Thus, if you drop a ball, or throw it vertically up in the air, it travels in a straight line, because the gravitational force acts parallel to the velocity of the particle.

We proceed to simplify the position-velocity-acceleration relations outlined in the preceding section for the special case of straight line motion.
For the particle shown in the picture, we would write

where s(t) is the distance traveled by the particle, v(t) is its speed and a(t) is the magnitude of its acceleration.
We often drop the basis vector i when solving problems involving straight line motion, but it is important to remember that s, v and a must all have the same sign convention.
Dropping the basis vector, then,

We can visualize these relationships graphically
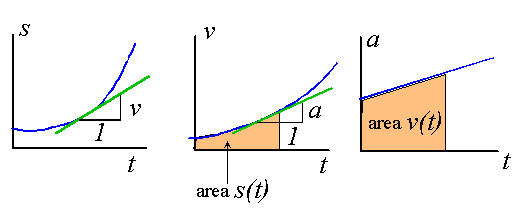
A useful alternative expression for acceleration
When we wrote down the velocity – acceleration relations in the preceding section, we assumed that we knew velocity as a function of time. It often happens that we don’t know v(t). Instead, we know the velocity of a particle as a function of distance traveled, v(s).
For example, one way you could measure the acceleration of a car would be to record its speed each time it passed a set of markers, placed a fixed distance apart.
You could then plot a graph showing the car’s speed as a function of its distance traveled, as shown. How do we deduce the car’s acceleration from this information?
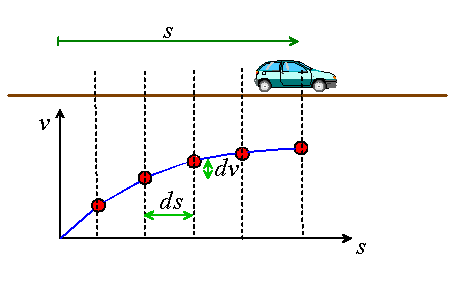
The graph shown above helps us to do this. Suppose the velocity increases by dv over a distance traveled ds. The time taken to travel this distance is dt=ds/v. Therefore, the acceleration is
![]()
Therefore, if we know the velocity as a function of position, the acceleration can be computed as
![]()
Calculating velocity and position from acceleration
Now, we return to our question. Given acceleration a, how do we find v and s? There are three general cases we need to deal with
(i) Given acceleration as a function of time a(t), find v(t) and s(t)
(ii) Given acceleration as a function of velocity a(v), find v(t) and s(t)
(iii) Given acceleration as a function of distance a(s), find v(t) and s(t).
In each case, we must also know the values of v and s at some time. Usually we know the values of v and s at time t=0.
Examples of these three cases are:
![]() Case
I: a(t) : a particle subjected to a prescribed force
Case
I: a(t) : a particle subjected to a prescribed force
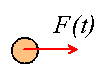
![]()
![]() Case
II: a(v) a particle falling through the air
Case
II: a(v) a particle falling through the air
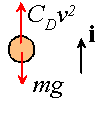
The particle is subjected to a gravitational force magnitude mg and a drag force
magnitude ![]() , as shown. Thus
, as shown. Thus

![]() Case
III: a(s) Spring-mass system
Case
III: a(s) Spring-mass system
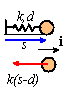
Suppose that the spring has un-stretched length d and stiffness k. If the spring is stretched to length s, it tries to return to its original length and in doing so exerts a force k(s-d) on the mass. Thus,

In each case, to compute v and s, we need to integrate the acceleration. You should already be familiar with the mathematical details. We will illustrate the procedure with a few examples.