Chapter 5
Vibrations
5.1 Overview of Vibrations
5.1.1 Examples of practical vibration
problems
Vibration
is a continuous cyclic motion of a structure or a component.
Generally,
engineers try to avoid vibrations, because vibrations have a number of
unpleasant effects:
·
Cyclic motion
implies cyclic forces. Cyclic forces are
very damaging to materials.
·
Even modest
levels of vibration can cause extreme discomfort;
·
Vibrations
generally lead to a loss of precision in controlling machinery.
Examples where vibration suppression is an issue
include:

Structural
vibrations. Most
buildings are mounted on top of special rubber pads, which are intended to
isolate the building from ground vibrations.
The figure on the right shows vibration isolators being installed under
the floor of a building during construction (from www.wilrep.com )
No vibrations course is complete
without a mention of the Tacoma Narrows suspension bridge. This bridge, constructed in the 1940s, was at
the time the longest suspension bridge in the world. Because it was a new design, it suffered from
an unforseen source of vibrations. In
high wind, the roadway would exhibit violent torsional vibrations, as shown in
the picture below.


You can watch newsreel footage of the
vibration and even the final collapse at http://www.youtube.com/watch?v=HxTZ446tbzE
To the credit of the designers, the bridge survived for an amazingly
long time before it finally failed. It is thought that the vibrations were a form
of self-excited vibration known as `flutter,’ or ‘galloping’ A similar form of vibration is known to occur
in aircraft wings.
Interestingly, modern cable stayed bridges that also suffer from a new
vibration problem: the cables are very lightly damped and can vibrate badly in
high winds (this is a resonance problem, not flutter). You can find a detailed
article on the subject at www.fhwa.dot.gov/bridge/pubs/05083/chap3.cfm. Some bridge designs
go as far as to incorporate active vibration suppression systems in their
cables.
 Vehicle
suspension systems are familiar to everyone, but continue to evolve as
engineers work to improve vehicle handling and ride (the figure above is from http://www.altairhyperworks.com. A radical
new approach to suspension design emerged in 2003 when a research group led by
Malcolm Smith at Cambridge University invented a new mechanical suspension
element they called an ‘inerter’. This
device can be thought of as a sort of generalized spring, but instead of
exerting a force proportional to the relative displacement of its two ends, the
inerter exerts a force that is proportional to the relative acceleration of its two ends. An actual realization is shown in the
figure. You can find a detailed
presentation on the theory behind the device at http://www-control.eng.cam.ac.uk/~mcs/lecture_j.pdf The device was adopted in secret by the McLaren
Formula 1 racing team in 2005 (they called it the ‘J damper’, and a scandal
erupted in Formula 1 racing when the Renault team managed to steal drawings for
the device, but were unable to work out what it does. The patent for the device has now been
licensed Penske and looks to become a standard element in formula 1
racing. It is only a matter of time
before it appears on vehicles available to the rest of us.
Vehicle
suspension systems are familiar to everyone, but continue to evolve as
engineers work to improve vehicle handling and ride (the figure above is from http://www.altairhyperworks.com. A radical
new approach to suspension design emerged in 2003 when a research group led by
Malcolm Smith at Cambridge University invented a new mechanical suspension
element they called an ‘inerter’. This
device can be thought of as a sort of generalized spring, but instead of
exerting a force proportional to the relative displacement of its two ends, the
inerter exerts a force that is proportional to the relative acceleration of its two ends. An actual realization is shown in the
figure. You can find a detailed
presentation on the theory behind the device at http://www-control.eng.cam.ac.uk/~mcs/lecture_j.pdf The device was adopted in secret by the McLaren
Formula 1 racing team in 2005 (they called it the ‘J damper’, and a scandal
erupted in Formula 1 racing when the Renault team managed to steal drawings for
the device, but were unable to work out what it does. The patent for the device has now been
licensed Penske and looks to become a standard element in formula 1
racing. It is only a matter of time
before it appears on vehicles available to the rest of us.
 Precision
Machinery: The picture on the right shows one example of a
precision instrument. It is essential
to isolate electron microscopes from vibrations. A typical transmission electron microscope is
designed to resolve features of materials down to atomic length scales. If the specimen vibrates by more than a few
atomic spacings, it will be impossible to see!
This is one reason that electron microscopes are always located in the
basement the basement of a building vibrates much less
than the upper floors. Professor K.-S. Kim at Brown recently invented
and patented a new vibration isolation system to support his atomic force
microscope on the 7th floor of the Barus-Holley building you can find the patent at United
States Patent, Patent Number 7,543,791.
Precision
Machinery: The picture on the right shows one example of a
precision instrument. It is essential
to isolate electron microscopes from vibrations. A typical transmission electron microscope is
designed to resolve features of materials down to atomic length scales. If the specimen vibrates by more than a few
atomic spacings, it will be impossible to see!
This is one reason that electron microscopes are always located in the
basement the basement of a building vibrates much less
than the upper floors. Professor K.-S. Kim at Brown recently invented
and patented a new vibration isolation system to support his atomic force
microscope on the 7th floor of the Barus-Holley building you can find the patent at United
States Patent, Patent Number 7,543,791.
Here is another precision instrument that is very
sensitive to vibrations.
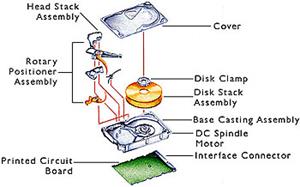 The picture shows features of a typical hard disk
drive. It is particularly important to
prevent vibrations in the disk stack assembly and in the disk head positioner,
since any relative motion between these two components will make it impossible
to read data. The spinning disk stack assembly has some very interesting
vibration characteristics (which fortunately for you, is beyond the scope of
this course).
The picture shows features of a typical hard disk
drive. It is particularly important to
prevent vibrations in the disk stack assembly and in the disk head positioner,
since any relative motion between these two components will make it impossible
to read data. The spinning disk stack assembly has some very interesting
vibration characteristics (which fortunately for you, is beyond the scope of
this course).
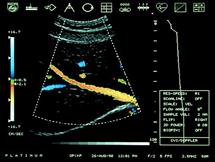 Vibrations are not always undesirable, however. On occasion, they can be put to good
use. Examples of beneficial applications
of vibrations include ultrasonic probes, both for medical application and for
nondestructive testing. The picture shows a
medical application of ultrasound: it is an image of someone’s colon. This type of instrument can resolve features
down to a fraction of a millimeter, and is infinitely preferable to exploratory
surgery. Ultrasound is also used to
detect cracks in aircraft and structures.
Vibrations are not always undesirable, however. On occasion, they can be put to good
use. Examples of beneficial applications
of vibrations include ultrasonic probes, both for medical application and for
nondestructive testing. The picture shows a
medical application of ultrasound: it is an image of someone’s colon. This type of instrument can resolve features
down to a fraction of a millimeter, and is infinitely preferable to exploratory
surgery. Ultrasound is also used to
detect cracks in aircraft and structures.
Musical instruments
and loudspeakers are a second example of systems which put vibrations to good
use. Finally, most mechanical clocks use
vibrations to measure time.
5.1.2 Vibration Measurement
 When faced with a vibration problem, engineers
generally start by making some measurements to try to isolate the cause of the
problem. There are two common ways to
measure vibrations:
When faced with a vibration problem, engineers
generally start by making some measurements to try to isolate the cause of the
problem. There are two common ways to
measure vibrations:
1. An accelerometer is a small electro-mechanical device
that gives an electrical signal proportional to its acceleration. The picture shows a typical 3 axis MEMS accelerometer
(you’ll use one in a project in this course).
MEMS accelerometers should be selected very carefully you can buy cheap accelerometers for less than
$50, but these are usually meant just as sensors, not for making precision
measurements. For measurements you’ll
need to select one that is specially designed for the frequency range you are
interested in sensing. The best
accelerometers are expensive ‘inertial grade’
versions (suitable for
so-called ‘inertial navigtation’ in which accelerations are integrated to
determine position) which are often use Kalman filtering to fuse the
accelerations with GPS measurements.
2. A displacement transducer is similar to an accelerometer,
but gives an electrical signal proportional to its displacement.
Displacement transducers are generally preferable if
you need to measure low frequency vibrations; accelerometers behave better at
high frequencies.
5.1.3 Features of a Typical Vibration Response
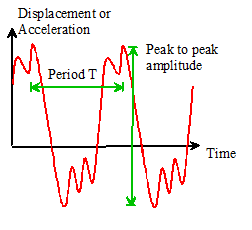
The
picture below shows a typical signal that you might record using an
accelerometer or displacement transducer.
Important features of the response are
 The signal is
often (although not always) periodic:
that is to say, it repeats itself at fixed intervals of time. Vibrations that do not repeat themselves in
this way are said to be random. All the systems we consider in this course
will exhibit periodic vibrations.
The signal is
often (although not always) periodic:
that is to say, it repeats itself at fixed intervals of time. Vibrations that do not repeat themselves in
this way are said to be random. All the systems we consider in this course
will exhibit periodic vibrations.
 The PERIOD of the signal, T, is the time required for
one complete cycle of oscillation, as shown in the picture.
The PERIOD of the signal, T, is the time required for
one complete cycle of oscillation, as shown in the picture.
 The FREQUENCY of
the signal, f, is the number of cycles of oscillation per
second. Cycles per second is often given the name Hertz: thus, a signal which
repeats 100 times per second is said to oscillate at 100 Hertz.
The FREQUENCY of
the signal, f, is the number of cycles of oscillation per
second. Cycles per second is often given the name Hertz: thus, a signal which
repeats 100 times per second is said to oscillate at 100 Hertz.
 The ANGULAR
FREQUENCY of the signal, ,
is defined as .
We specify angular frequency in radians per second. Thus, a signal that oscillates at 100 Hz has
angular frequency radians per second.
The ANGULAR
FREQUENCY of the signal, ,
is defined as .
We specify angular frequency in radians per second. Thus, a signal that oscillates at 100 Hz has
angular frequency radians per second.
 Period, frequency
and angular frequency are related by
Period, frequency
and angular frequency are related by
 The PEAK-TO-PEAK
AMPLITUDE of the signal, A, is the difference between its maximum value and
its minimum value, as shown in the picture
The PEAK-TO-PEAK
AMPLITUDE of the signal, A, is the difference between its maximum value and
its minimum value, as shown in the picture
 The AMPLITUDE
of the signal is generally taken to mean half its peak to peak amplitude.
Engineers sometimes use amplitude as an abbreviation for peak to peak
amplitude, however, so be careful.
The AMPLITUDE
of the signal is generally taken to mean half its peak to peak amplitude.
Engineers sometimes use amplitude as an abbreviation for peak to peak
amplitude, however, so be careful.
 The ROOT MEAN
SQUARE AMPLITUDE or RMS amplitude is defined as
The ROOT MEAN
SQUARE AMPLITUDE or RMS amplitude is defined as
5.1.4 Harmonic Oscillations
Harmonic oscillations are a particularly simple form
of vibration response. A conservative
spring-mass system will exhibit harmonic motion if you have Java, Internet Explorer (or a
browser plugin that allows you to run IE in another browser) you can run a Java
Applet to visualize the motion. You can
find instructions for installing Java, the IE plugins, and giving permission
for the Applet to run here. The address
for the SHM simulator (cut and paste this into the Internet Explorer address
bar)
http://www.brown.edu/Departments/Engineering/Courses/En4/java/shm.html
If the spring is perturbed from its static equilibrium
position, it vibrates (press `start’ to watch the vibration). We will analyze the motion of the spring mass
system soon. We will find that the displacement of the mass from its static
equilibrium position, ,
has the form
Here, is
the amplitude of the displacement, is the frequency of oscillations in radians
per second, and (in radians) is known as the `phase’ of the
vibration. Vibrations of this form are
said to be Harmonic.
Typical values for amplitude and frequency are listed
in the table below
|
|
Frequency /Hz
|
Amplitude/mm
|
|
Atomic Vibration
|
|
|
|
Threshold of human perception
|
1-8
|
|
|
Machinery and building vibes
|
10-100
|
|
|
Swaying of tall buildings
|
1-5
|
10-1000
|
We can also express the displacement in terms of its
period of oscillation T
The velocity and acceleration of the mass follow as
Here, is the amplitude of the velocity, and is the amplitude of the acceleration. Note the simple relationships between
acceleration, velocity and displacement amplitudes.
Surprisingly, many complex engineering systems behave
just like the spring mass system we are looking at here. To describe the behavior of the system, then,
we need to know three things (in order of importance):
(1) The frequency (or period) of the vibrations
(2) The amplitude of the vibrations
(3) Occasionally, we might be interested in the phase,
but this is rare.
So, our next problem is to find a way to calculate
these three quantities for engineering systems.
We will do this in stages. First, we will analyze a number of freely
vibrating, conservative systems. Second,
we will examine free vibrations in a dissipative system, to show the influence
of energy losses in a mechanical system.
Finally, we will discuss the behavior of mechanical systems when they
are subjected to oscillating forces.
5.2 Free vibration
of conservative, single degree of freedom, linear systems.
First, we will explain what is meant by the title of
this section.
 Recall that a
system is conservative if energy is
conserved, i.e. potential energy + kinetic energy = constant during motion.
Recall that a
system is conservative if energy is
conserved, i.e. potential energy + kinetic energy = constant during motion.
 Free vibration means that no
time varying external forces act on the system.
Free vibration means that no
time varying external forces act on the system.
 A system has one degree of freedom if its motion can
be completely described by a single scalar variable. We’ll discuss this in a bit more detail
later.
A system has one degree of freedom if its motion can
be completely described by a single scalar variable. We’ll discuss this in a bit more detail
later.
 A system is said to be linear if its equation of motion is linear. We will see what this means shortly.
A system is said to be linear if its equation of motion is linear. We will see what this means shortly.
It turns out that all 1DOF, linear conservative
systems behave in exactly the same way.
By analyzing the motion of one representative system, we can learn about
all others.
We will follow
standard procedure, and use a spring-mass system as our representative example.
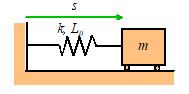
Problem: The figure shows a spring mass system. The spring has stiffness k and unstretched length . The mass is released with velocity from position at time . Find .
There is a standard approach to solving problems like
this
(i) Get a differential equation for s using F=ma (or other methods to be discussed)
(ii) Solve the differential equation.
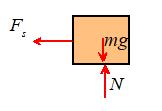
The picture shows a free body diagram for the mass.
Newton’s law of
motion states that
The spring force is related to the length of the
spring by . The i component
of the equation of motion and this equation then shows that
This is our equation of motion for s.
Now, we need to solve this equation. We could, of course, use Matlab to do this in fact here is the Matlab solution.
syms m
k L0 s0 v0 real
syms v(t)
s(t)
assume(k>0); assume(m>0);
diffeq = m*diff(s(t),t,2) + k*s(t) == k*L0;
v(t) = diff(s(t),t);
IC = [s(0)==s0, v(0)==v0];
s(t) = dsolve(diffeq,IC)
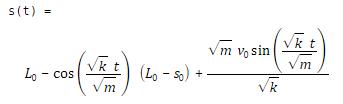
In practice we usually don’t need to use matlab (and
of course in exams you won’t have access to matlab!)
5.2.1 Using tabulated solutions to solve equations of motion for
vibration problems
Note
that all vibrations problems have similar equations of motion. Consequently, we can just solve the equation
once, record the solution, and use it to solve any vibration problem we might
be interested in. The procedure to solve
any vibration problem is:
1. Derive
the equation of motion, using Newton’s laws (or sometimes you can use energy
methods, as discussed in Section 5.3)
2. Do
some algebra to arrange the equation of motion into a standard form
3. Look
up the solution to this standard form in a table of solutions to vibration
problems.
We
have provided a table of standard solutions as a separate document that you can
download and print for future reference. Actually, this is exactly what MATLAB is
doing when it solves a differential equation for you it is doing sophisticated pattern matching to
look up the solution you want in a massive internal database.
We will illustrate the
procedure using many examples.
 5.2.2
Solution to the equation of motion for an undamped spring-mass system
5.2.2
Solution to the equation of motion for an undamped spring-mass system
We
would like to solve
with
initial conditions from position at time .
We
therefore consult our list of solutions to differential equations, and observe
that it gives the solution to the following equation
This
is very similar to our equation, but not quite the same. To make them identical, divide our equation
through by k
We see that if we define
then our equation is equivalent to the standard one.
HEALTH
WARNING: it is important to note that this substitution only
works if is constant, so its time derivative is zero.
The
solution for x is
Here, and are the initial value of x and its time derivative, which must be computed
from the initial values of s and its
time derivative
When we present the solution, we have a choice of
writing down the solution for x, and
giving formulas for the various terms in the solution (this is what is usually
done):
Alternatively, we can express all the variables in the
standard solution in terms of s
But this solution looks very messy (more like the Matlab
solution).
Observe that:
 The mass
oscillates harmonically, as discussed in the preceding section;
The mass
oscillates harmonically, as discussed in the preceding section;
 The angular frequency of oscillation, ,
is a characteristic property of the system, and is independent of the initial
position or velocity of the mass. This
is a very important observation, and we will expand upon it below. The characteristic frequency is known as the natural frequency of the system.
The angular frequency of oscillation, ,
is a characteristic property of the system, and is independent of the initial
position or velocity of the mass. This
is a very important observation, and we will expand upon it below. The characteristic frequency is known as the natural frequency of the system.
 Increasing the stiffness of the spring increases the
natural frequency of the system;
Increasing the stiffness of the spring increases the
natural frequency of the system;
 Increasing the mass reduces the natural frequency of
the system.
Increasing the mass reduces the natural frequency of
the system.
5.2.3
Natural Frequencies and Mode Shapes.
We saw that the spring mass system described in the
preceding section likes to vibrate at a characteristic frequency, known as its natural frequency. This turns out to be
a property of all stable mechanical systems.
All stable, unforced, mechanical systems
vibrate harmonically at certain discrete frequencies, known as natural
frequencies of the system.
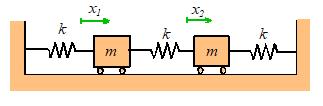 For the springmass system, we
found only one natural frequency. More
complex systems have several natural frequencies. For example, the system of two masses shown
below has two natural frequencies, given by
For the springmass system, we
found only one natural frequency. More
complex systems have several natural frequencies. For example, the system of two masses shown
below has two natural frequencies, given by
A system with three
masses would have three natural frequencies, and so on.
In general, a system with more than one natural frequency will not
vibrate harmonically.
For example, suppose
we start the two mass system vibrating, with initial conditions
 The response may be shown (see sect 5.5 if you
want to know how) to be
The response may be shown (see sect 5.5 if you
want to know how) to be
with
In general, the vibration response will look
complicated, and is not harmonic. The animation above shows a typical example (if
you are using the pdf version of these notes the animation will not work)
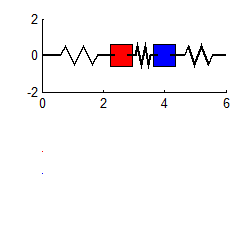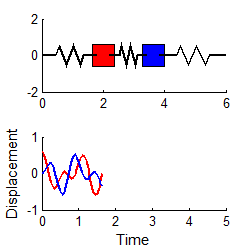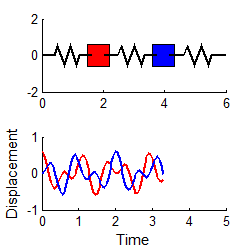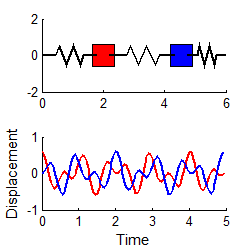
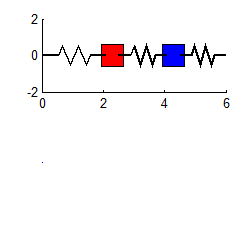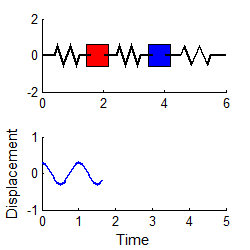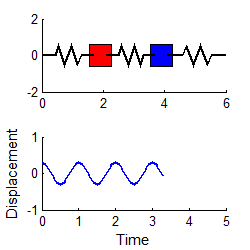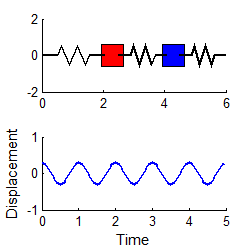 However, if we
choose the special initial conditions:
However, if we
choose the special initial conditions:
then the response is simply
i.e., both masses vibrate harmonically, at the first
natural frequency, as shown in the animation to the right.
Similarly, if we choose
then
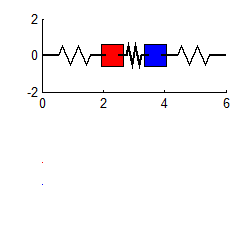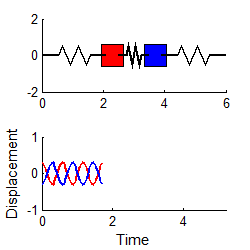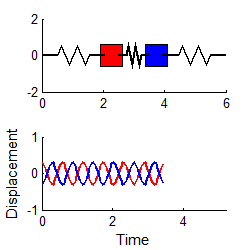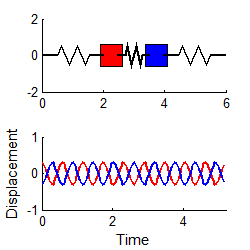
i.e., the system vibrates harmonically, at the second
natural frequency.
The special initial displacements of a
system that cause it to vibrate harmonically are called `mode shapes’ for the system.
If a system has several natural frequencies, there is
a corresponding mode of vibration
for each natural frequency.
The natural
frequencies are arguably the single most important property of any mechanical
system. This is
because, as we shall see, the natural frequencies coincide (almost) with the
system’s resonant frequencies. That is to say, if you apply a time varying
force to the system, and choose the frequency of the force to be equal to one
of the natural frequencies, you will observe very large amplitude vibrations.
When designing a structure or component, you generally
want to control its natural vibration frequencies very carefully. For example, if you wish to stop a system
from vibrating, you need to make sure that all its natural frequencies are much
greater than the expected frequency of any forces that are likely to act on the
structure. If you are designing a
vibration isolation platform, you generally want to make its natural frequency
much lower than the vibration frequency of the floor that it will stand on. Design codes usually specify allowable ranges
for natural frequencies of structures and components.
Once a prototype has been built, it is usual to
measure the natural frequencies and mode shapes for a system. This is done by attaching a number of
accelerometers to the system, and then hitting it with a hammer (this is
usually a regular rubber tipped hammer, which might be instrumented to measure
the impulse exerted by the hammer during the impact). By trial and error, one can find a spot to
hit the device so as to excite each mode of vibration independent of any
other. You can tell when you have found
such a spot, because the whole system vibrates harmonically. The natural frequency and mode shape of each
vibration mode is then determined from the accelerometer readings.
Impulse hammer tests can even be used on big
structures like bridges or buildings but you need a big hammer. In a recent test on a new cable stayed bridge
in France, the bridge was excited by first attaching a barge to the center span
with a high strength cable; then the cable was tightened to raise the barge
part way out of the water; then, finally, the cable was released rapidly to set
the bridge vibrating.
5.2.4
Calculating the number of degrees of freedom (and natural frequencies) of a
system
When you analyze the behavior a system, it is helpful
to know ahead of time how many vibration frequencies you will need to
calculate. There are various ways to do
this. Here are some rules that you can
apply:
The number
of degrees of freedom is equal to the number of independent coordinates
required to describe the motion.
This is only helpful if you can see by inspection how to describe your
system. For the spring-mass system in
the preceding section, we know that the mass can only move in one direction,
and so specifying the length of the spring s
will completely determine the motion of the system. The system therefore has one degree of
freedom, and one vibration frequency.
Section 5.6 provides several more examples where it is fairly obvious
that the system has one degree of freedom.
For a 2D system, the number of degrees
of freedom can be calculated from the equation
where:
is the number of rigid bodies in the
system
p is the number of
particles in the system
is the number of constraints (or, if you
prefer, independent reaction forces) in the system.
To be able to apply this formula you need to know how
many constraints appear in the problem.
Constraints are imposed by things like rigid links, or contacts with
rigid walls, which force the system to move in a particular way. The numbers of constraints associated with
various types of 2D connections are listed in the table below. Notice that the number of constraints is
always equal to the number of reaction forces you need to draw on an FBD to
represent the joint
|
Roller joint
1 constraint (prevents motion in
one direction)
|
|
|
Rigid (massless) link (if the link has mass, it should be
represented as a rigid body)
1 constraint (prevents relative
motion parallel to link)
|
|
|
Nonconformal contact (two bodies meet at a point)
No friction or slipping: 1 constraint (prevents
interpenetration)
Sticking friction 2 constraints (prevents relative motion
|

|
|
Conformal contact (two rigid bodies meet along a line)
No friction or slipping: 2 constraint (prevents
interpenetration and rotation)
Sticking friction 3 constraints (prevents relative motion)
|
|
|
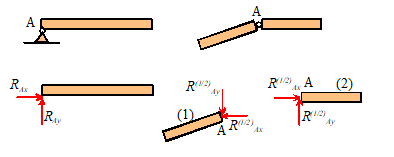
Pinned joint (generally only applied to a rigid body, as it
would stop a particle moving completely)
2 constraints (prevents motion
horizontally and vertically)
|
|
|
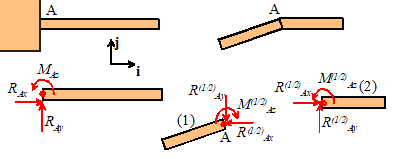
Clamped joint (rare in dynamics problems, as it prevents motion
completely)
Can only be applied to a rigid
body, not a particle
3 constraints (prevents motion
horizontally, vertically and prevents rotation)
|
|
For a 3D system, the number of degrees
of freedom can be calculated from the equation
where the symbols have the same meaning as for a 2D
system. A table of various constraints
for 3D problems is given below.
|
Pinned
joint
(5 constraints prevents all motion, and prevents rotation
about two axes)
|
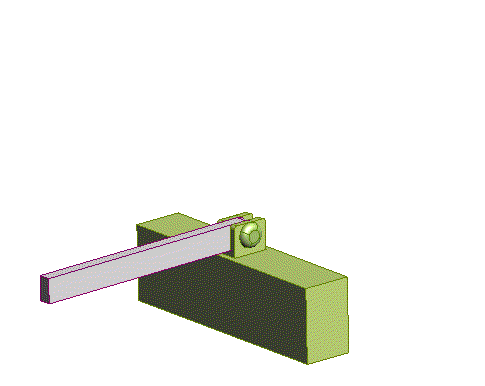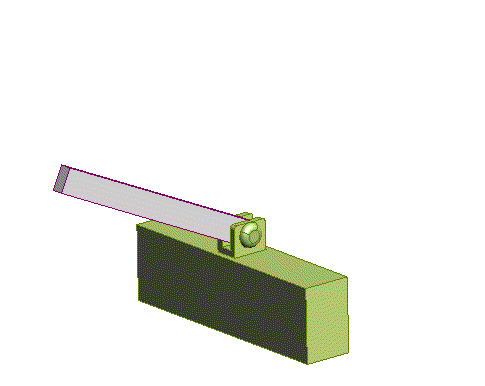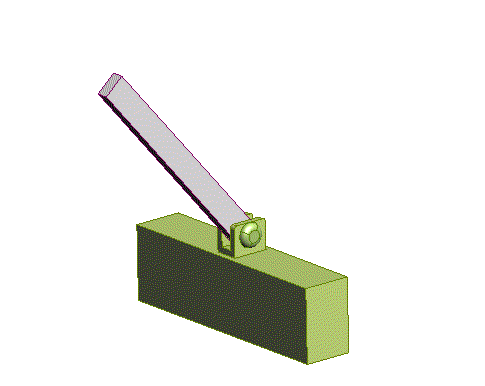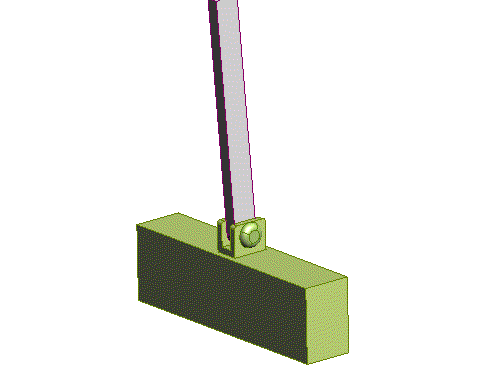
|
|
Roller
bearing
(5 constraints prevents all motion, and prevents rotation
about two axes)
|
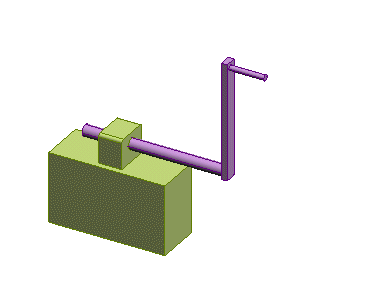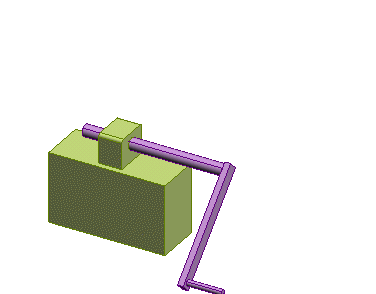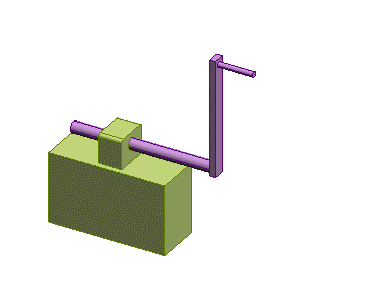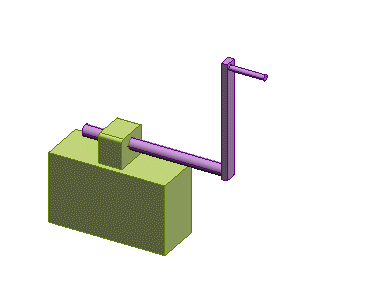
|
|
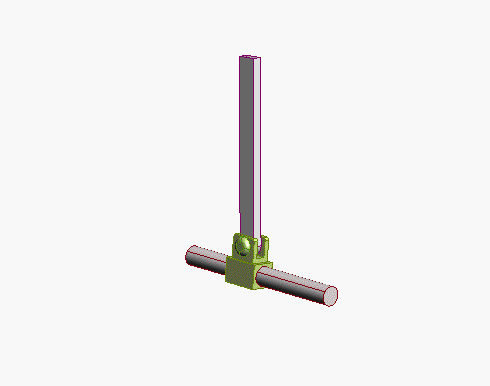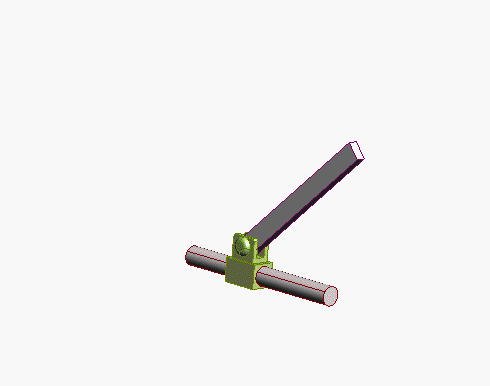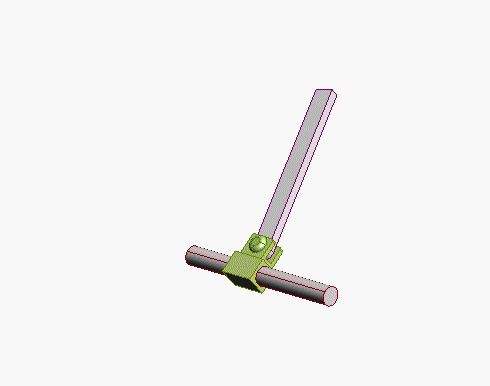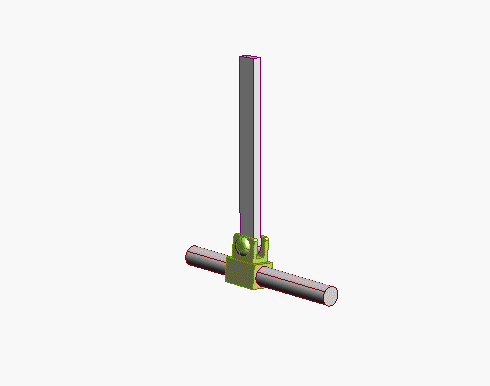
Sleeve
(4 constraints prevents motion in two directions, and
prevents rotation about two axes)
|
|
|
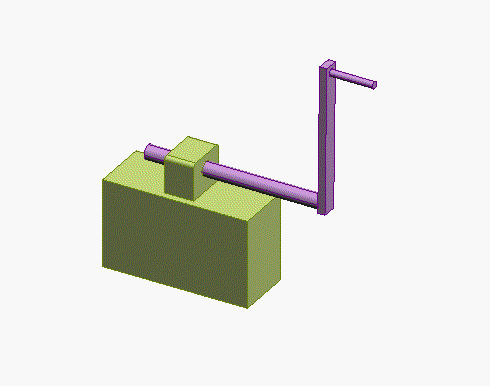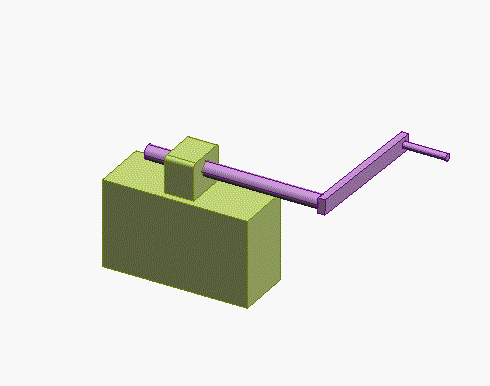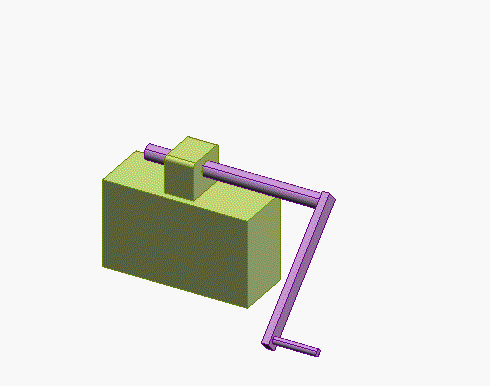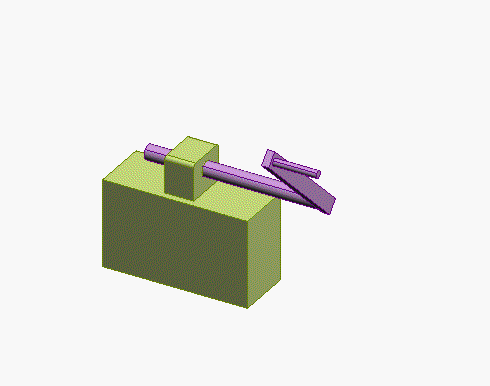
Swivel
joint
4 constraints (prevents all motion, prevents
rotation about 1 axis)
|
|
|
Ball and
socket joint
3 constraints prevents all motion.
|
|
|
Nonconformal
contact (two rigid bodies meet at a point)
No
friction or slipping: 1 constraint (prevents interpenetration)
Sticking
friction 3 constraints, possibly 4 if friction is sufficient
to prevent spin at contact)
|
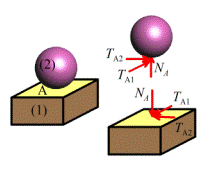
|
|
Conformal
contact (two rigid bodies meet over a surface)
No
friction or slipping: 3 constraints: prevents interpenetration and
rotation about two axes.
Sticking: 6 constraints:
prevents all relative motion and rotation.
|
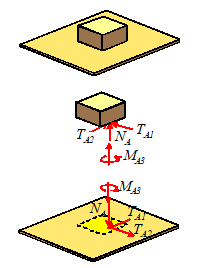
|
|
Clamped
joint (rare in dynamics problems, as it prevents all
motion)
6 constraints (prevents all motion and rotation)
|

|
5.2.4
Calculating natural frequencies for 1DOF conservative systems
In light of the discussion in the preceding section,
we clearly need some way to calculate natural frequencies for mechanical
systems. We do not have time in this
course to discuss more than the very simplest mechanical systems. We will therefore show you some tricks for
calculating natural frequencies of 1DOF, conservative, systems. It is best to
do this by means of examples.
Example 1: The spring-mass system revisited
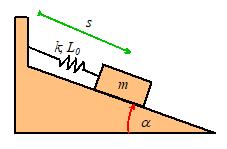
Calculate the natural frequency of vibration for the
system shown in the figure. Assume that the contact between the block and wedge
is frictionless. The spring has
stiffness k and unstretched length
Our first
objective is to get an equation of motion for s. We could do this by
drawing a FBD, writing down Newton’s law, and looking at its components. However, for 1DOF systems it turns out that
we can derive the EOM very quickly using the kinetic and potential energy of
the system.
The potential energy and kinetic energy can be written
down as:
(The second term in V is the gravitational potential energy it is negative because the height of the mass
decreases with increasing s). Now,
note that since our system is
conservative
Differentiate our expressions for T and V (use the chain
rule) to see that
Finally, we must turn this equation of motion into one
of the standard solutions to vibration equations.
Our equation looks very similar to
By comparing this with our equation we see that the
natural frequency of vibration is
Summary of procedure for calculating
natural frequencies:
(1) Describe the motion of the system, using a
single scalar variable (In the example, we chose to describe motion using the
distance s);
(2) Write
down the potential energy V and kinetic energy T of the
system in terms of the scalar variable;
(3) Use to get an equation of motion for your scalar
variable;
(4) Arrange
the equation of motion in standard form;
(5) Read off
the natural frequency by comparing your equation to the standard form.
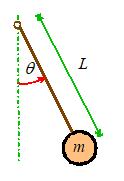
Example 2: A nonlinear system.
We will illustrate the procedure with a second
example, which will demonstrate another useful trick.
Find the natural frequency of vibration for a
pendulum, shown in the figure.
We will idealize the mass as a particle, to keep
things simple.
We will follow the steps outlined earlier:
(1) We describe
the motion using the angle
(2) We write
down T and V:
(if you don’t see the formula for the kinetic energy,
you can write down the position vector of the mass as ,
differentiate to find the velocity: ,
and then compute and use a trig identity. You can also use the circular motion
formulas, if you prefer).
(3) Differentiate with respect to time:
(4) Arrange the EOM into standard form. Houston, we have a problem. There is no way this equation can be arranged
into standard form. This is because the
equation is nonlinear ( is a nonlinear function of ).
There is, however, a way to deal with this problem. We will show what needs to be done,
summarizing the general steps as we go along.
(i) Find the static equilibrium
configuration(s) for the system.
If the system is in static equilibrium, it
does not move. We can find values of for which the system is in static equilibrium
by setting all time derivatives of in the equation of motion to zero, and then
solving the equation. Here,
Here, we have
used to denote the special values of for which the system happens to be in static
equilibrium. Note that is always a constant.
(ii) Assume
that the system vibrates with small amplitude about a static equilibrium
configuration of interest.
To do this, we let ,
where .
Here, x represents a small change in angle
from an equilibrium configuration.. Note that x will vary with time as the system vibrates. Instead of solving for ,
we will solve for x. Before going on, make sure that you are
comfortable with the physical significance of
both x and .
(iii)
Linearize the equation of motion, by expanding all nonlinear terms as Taylor
Maclaurin series about the equilibrium configuration.
We substitute for in the equation of motion, to see that
(Recall that is constant, so its time derivatives vanish)
Now, recall the Taylor-Maclaurin series expansion of a
function f(x) has the form
where
Apply this to the nonlinear term in our equation of
motion
Now, since x<<1,
we can assume that ,
and so
Finally, we can substitute back into our equation of
motion, to obtain
(iv) Compare
the linear equation with the standard form to deduce the natural frequency.
We can do this for each equilibrium configuration.
whence
Note that all
these values of really represent the same configuration: the
mass is hanging below the pivot. We have
rediscovered the well-known expression for the natural frequency of a freely
swinging pendulum.
Next, try the remaining static equilibrium
configuration
If we look up
this equation in our list of standard solutions, we find it does not have a
harmonic solution. Instead, the solution
is
where and
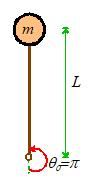 Thus, except for some rather special initial
conditions, x increases without bound
as time increases. This is a
characteristic of an unstable mechanical
system.
Thus, except for some rather special initial
conditions, x increases without bound
as time increases. This is a
characteristic of an unstable mechanical
system.
If we visualize
the system with ,
we can see what is happening. This
equilibrium configuration has the pendulum upside down!
No wonder the equation is predicting
an instability…
Here
is a question to think about. Our
solution predicts that both x and dx/dt
become infinitely large. We know
that a real pendulum would never rotate with infinite angular velocity. What has gone wrong?
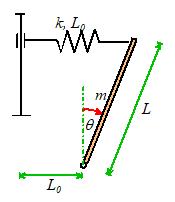
Example 3:
We will look at one more nonlinear system, to make sure that you are
comfortable with this procedure. Calculate the resonant frequency of small
oscillations about the equilibrium configuration for the system shown. The spring has
stiffness k and unstretched length .
We follow the same procedure as
before.
The potential and kinetic energies of the system are
Hence
Once again, we have found a nonlinear equation of
motion. This time we know what to
do. We are told to find natural
frequency of oscillation about ,
so we don’t need to solve for the equilibrium configurations this time. We set ,
with and substitute back into the equation of
motion:
Now, expand all the nonlinear terms (it is OK to do
them one at a time and then multiply everything out. You can always throw away all powers of x greater than one as you do so)
We now have an equation in standard form, and can read
off the natural frequency
Question: what happens for ?
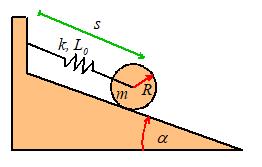 Example 3: A system with
a rigid body (the KE of a rigid body will be defined in the next section of the
course just live with it for now!).
Example 3: A system with
a rigid body (the KE of a rigid body will be defined in the next section of the
course just live with it for now!).
Calculate
the natural frequency of vibration for the system shown in the figure. Assume that the cylinder rolls without slip
on the wedge. The spring has stiffness k and
unstretched length
Our first objective is to
get an equation of motion for s. We do this by writing down the potential and
kinetic energies of the system in terms of s.
The potential energy is
easy:
The first term represents
the energy in the spring, while second term accounts for the gravitational
potential energy.
The
kinetic energy is slightly more tricky.
Note that the magnitude of the angular velocity of the disk is related
to the magnitude of its translational velocity by
Thus, the combined
rotational and translational kinetic energy follows as
Now, note that since our
system is conservative
Differentiate our
expressions for T and V to see that
The last equation is almost
in one of the standard forms given on the handout, except that the right hand
side is not zero. There is a trick to
dealing with this problem simply subtract the constant right hand side
from s, and call the result x.
(This only works if the right hand side is a constant, of course). Thus let
and substitute into the
equation of motion:
This is now in the form
and by comparing this with
our equation we see that the natural frequency of vibration is
5.3 Free vibration of a damped, single degree of
freedom, linear spring mass system.
We
analyzed vibration of several conservative systems in the preceding
section. In each case, we found that if
the system was set in motion, it continued to move indefinitely. This is counter to our everyday
experience. Usually, if you start
something vibrating, it will vibrate with a progressively decreasing amplitude
and eventually stop moving.
The
reason our simple models predict the wrong behavior is that we neglected energy
dissipation. In this section, we explore
the influence of energy dissipation on free vibration of a spring-mass
system. As before, although we model a
very simple system, the behavior we predict turns out to be representative of a
wide range of real engineering systems.
5.3.1 Vibration of a damped spring-mass
system
The
spring mass dashpot system shown is released with velocity from position at time . Find .
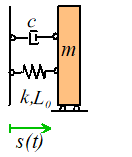
Once
again, we follow the standard approach to solving problems like this
(i)
Get a differential equation for s
using F=ma
(ii)
Solve the differential equation.
You
may have forgotten what a dashpot (or damper) does. Suppose we apply a force F to a dashpot, as shown in the figure. We would observe
that the dashpot stretched at a rate proportional to the force
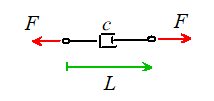
One
can buy dampers (the shock absorbers in your car contain dampers): a damper
generally consists of a plunger inside an oil filled cylinder, which dissipates
energy by churning the oil. Thus, it is
possible to make a spring-mass-damper system that looks very much like the one
in the picture. More generally, however,
the spring mass system is used to represent a complex mechanical system. In this case, the damper represents the
combined effects of all the various mechanisms for dissipating energy in the
system, including friction, air resistance, deformation losses, and so on.
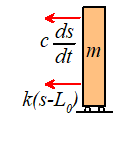
To proceed, we draw a free
body diagram, showing the forces exerted by the spring and damper on the mass.
Newton’s law then states
that
This is our equation of motion for s.
Now, we check our list of solutions to differential
equations, and see that we have a solution to:
We can get our equation
into this form by setting
As before, is known as the natural frequency of the
system. We have discovered a new
parameter, ,
which is called the damping coefficient. It plays a very important role, as we shall
see below.
Now, we can write down the
solution for x:
Overdamped System
where
Critically Damped System
Underdamped System
where is known as the damped natural frequency of
the system.
In all the preceding
equations, are the values of x and its time derivative at time t=0.
These
expressions are rather too complicated to visualize what the system is doing
for any given set of parameters. if you have Java, Internet Explorer (or a
browser plugin that allows you to run IE in another browser) you can run a Java
Applet to visualize the motion. You can
find instructions for installing Java, the IE plugins, and giving permission
for the Applet to run here. The address for the free vibration simulator
(cut and paste this into the Internet Explorer address bar) is
http://www.brown.edu/Departments/Engineering/Courses/En4/java/free.html
You
can use the sliders to set the values of either m, k, and (in this case the program will calculate the
values of and for you, and display the results), or
alternatively, you can set the values of and directly.
You can also choose values for the initial conditions and . When you press `start,’ the applet will
animate the behavior of the system, and will draw a graph of the position of
the mass as a function of time. You can
also choose to display the phase plane, which shows the velocity of the mass as
a function of its position, if you wish.
You can stop the animation at any time, change the parameters, and plot
a new graph on top of the first to see what has changed. If you press `reset’, all your graphs will be
cleared, and you can start again.
Try the following tests to
familiarize yourself with the behavior of the system
 Set the dashpot
coefficient to a low value, so that the damping
coefficient . Make sure the graph is set to display
position versus time, and press `start.’ You should see the system
vibrate. The vibration looks very similar to the
behavior of the conservative system we analyzed in the preceding section,
except that the amplitude decays with time.
Note that the system vibrates at a frequency very slightly lower than
the natural frequency of the system.
Set the dashpot
coefficient to a low value, so that the damping
coefficient . Make sure the graph is set to display
position versus time, and press `start.’ You should see the system
vibrate. The vibration looks very similar to the
behavior of the conservative system we analyzed in the preceding section,
except that the amplitude decays with time.
Note that the system vibrates at a frequency very slightly lower than
the natural frequency of the system.
 Keeping the value
of fixed, vary the values of spring constant and
mass to see what happens to the frequency of vibration and also to the rate of
decay of vibration. Is the behavior
consistent with the solutions given above?
Keeping the value
of fixed, vary the values of spring constant and
mass to see what happens to the frequency of vibration and also to the rate of
decay of vibration. Is the behavior
consistent with the solutions given above?
 Keep the values of k and m fixed, and vary . You should see that, as you increase ,
the vibration dies away more and more quickly.
What happens to the frequency of oscillations as is increased?
Is this behavior consistent with the predictions of the theory?
Keep the values of k and m fixed, and vary . You should see that, as you increase ,
the vibration dies away more and more quickly.
What happens to the frequency of oscillations as is increased?
Is this behavior consistent with the predictions of the theory?
 Now, set the damping coefficient (not the
dashpot coefficient this time) to . For this value, the system no longer
vibrates; instead, the mass smoothly returns to its equilibrium position x=0.
If you need to design a system that returns to its equilibrium position
in the shortest possible time, then it is customary to select system parameters so that . A system of this kind is said to be critically damped.
Now, set the damping coefficient (not the
dashpot coefficient this time) to . For this value, the system no longer
vibrates; instead, the mass smoothly returns to its equilibrium position x=0.
If you need to design a system that returns to its equilibrium position
in the shortest possible time, then it is customary to select system parameters so that . A system of this kind is said to be critically damped.
 Set to a value greater than 1. Under these conditions, the system decays
more slowly towards its equilibrium configuration.
Set to a value greater than 1. Under these conditions, the system decays
more slowly towards its equilibrium configuration.
 Keeping >1, experiment with the effects of changing
the stiffness of the spring and the value of the mass. Can you explain what is happening
mathematically, using the equations of motion and their solution?
Keeping >1, experiment with the effects of changing
the stiffness of the spring and the value of the mass. Can you explain what is happening
mathematically, using the equations of motion and their solution?
 Finally, you might like to look at the
behavior of the system on its phase plane.
In this course, we will not make much use of the phase plane, but it is
a powerful tool for visualizing the behavior of nonlinear systems. By looking at the patterns traced by the
system on the phase plane, you can often work out what it is doing. For example, if the trajectory encircles the
origin, then the system is vibrating. If
the trajectory approaches the origin, the system is decaying to its equilibrium
configuration.
Finally, you might like to look at the
behavior of the system on its phase plane.
In this course, we will not make much use of the phase plane, but it is
a powerful tool for visualizing the behavior of nonlinear systems. By looking at the patterns traced by the
system on the phase plane, you can often work out what it is doing. For example, if the trajectory encircles the
origin, then the system is vibrating. If
the trajectory approaches the origin, the system is decaying to its equilibrium
configuration.
We
now know the effects of energy dissipation on a vibrating system. One important conclusion is that if the
energy dissipation is low, the system will vibrate. Furthermore, the frequency of vibration is
very close to that of an undamped system. Consequently, if you want to predict
the frequency of vibration of a system, you can simplify the calculation by
neglecting damping.
5.3.2 Using Free Vibrations to Measure
Properties of a System
We
will describe one very important application of the results developed in the
preceding section.
It
often happens that we need to measure the dynamical properties of an
engineering system. For example, we
might want to measure the natural frequency and damping coefficient for a
structure after it has been built, to make sure that design predictions were
correct, and to use in future models of the system.
You
can use the free vibration response to do this, as follows. First, you
instrument your design by attaching accelerometers to appropriate points. You then use an impulse hammer to excite a
particular mode of vibration, as discussed in Section 5.1.3. You use your accelerometer readings to
determine the displacement at the point where the structure was excited: the
results will be a graph similar to the one shown below.
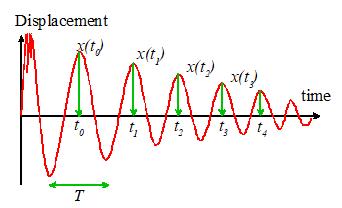
We then identify a nice
looking peak, and call the time there ,
as shown.
The following quantities
are then measured from the graph:
1. The period of oscillation. The period of oscillation was defined
in Section 5.1.2: it is the time between two peaks, as shown. Since the signal is (supposedly) periodic, it
is often best to estimate T as follows
where is the time at which the nth peak occurs, as shown in the picture.
2. The Logarithmic Decrement.
This is a new quantity, defined as follows
where is the displacement at the nth peak, as shown. In principle, you should be able to pick any
two neighboring peaks, and calculate . You should get the same answer, whichever
peaks you choose. It is often more
accurate to estimate using the following formula
This expression should give
the same answer as the earlier definition.
Now, it turns out that we
can deduce and from T
and ,
as follows.
Why
does this work? Let us calculate T
and using the exact solution to the equation of
motion for a damped spring-mass system.
Recall that, for an underdamped system, the solution has the form
where .
Hence, the period of oscillation is
Similarly,
where we have noted that .
Fortunately, this horrendous equation can be simplified
greatly: substitute for T in terms of and ,
then cancel everything you possibly can to see that
Finally, we can solve for and to see that:
as promised.
Note that this procedure can
never give us values for k, m or . However, if we wanted to find these, we could
perform a static test on the structure.
If we measure the deflection d
under a static load F, then we know
that
Once k had been
found, m and are easily deduced from the relations
5.4 Forced vibration of damped, single degree of
freedom, linear spring mass systems.
 Finally, we solve the most important vibration
problems of all. In engineering
practice, we are almost invariably interested in predicting the response of a
structure or mechanical system to external forcing. For example, we may need to predict the
response of a bridge or tall building to wind loading, earthquakes, or ground
vibrations due to traffic. Another
typical problem you are likely to encounter is to isolate a sensitive system
from vibrations. For example, the
suspension of your car is designed to isolate a sensitive system (you) from
bumps in the road. Electron microscopes
are another example of sensitive instruments that must be isolated from
vibrations. Electron microscopes are designed
to resolve features a few nanometers in size.
If the specimen vibrates with amplitude of only a few nanometers, it
will be impossible to see! Great care is
taken to isolate this kind of instrument from vibrations. That is one reason they are almost always in
the basement of a building: the basement vibrates much less than the floors
above.
Finally, we solve the most important vibration
problems of all. In engineering
practice, we are almost invariably interested in predicting the response of a
structure or mechanical system to external forcing. For example, we may need to predict the
response of a bridge or tall building to wind loading, earthquakes, or ground
vibrations due to traffic. Another
typical problem you are likely to encounter is to isolate a sensitive system
from vibrations. For example, the
suspension of your car is designed to isolate a sensitive system (you) from
bumps in the road. Electron microscopes
are another example of sensitive instruments that must be isolated from
vibrations. Electron microscopes are designed
to resolve features a few nanometers in size.
If the specimen vibrates with amplitude of only a few nanometers, it
will be impossible to see! Great care is
taken to isolate this kind of instrument from vibrations. That is one reason they are almost always in
the basement of a building: the basement vibrates much less than the floors
above.
We
will again use a spring-mass system as a model of a real engineering
system. As before, the spring-mass
system can be thought of as representing a single mode of vibration in a real
system, whose natural frequency and damping coefficient coincide with that of
our spring-mass system.
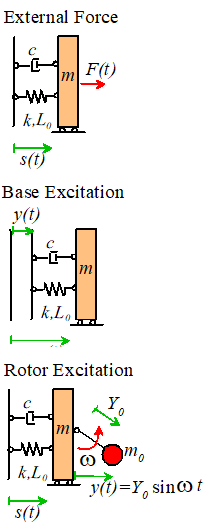
We will consider three
types of forcing applied to the spring-mass system, as shown below:
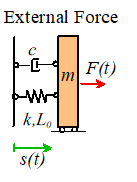
External Forcing models the behavior of a system which has a time
varying force acting on it. An example
might be an offshore structure subjected to wave loading.
Base Excitation models the behavior of a vibration isolation
system. The base of the spring is given
a prescribed motion, causing the mass to vibrate. This system can be used to model a vehicle
suspension system, or the earthquake response of a structure.
Rotor Excitation models the effect of a rotating machine mounted on a
flexible floor. The crank with length and mass rotates at constant angular velocity, causing
the mass m to vibrate.
Of
course, vibrating systems can be excited in other ways as well, but the
equations of motion will always reduce to one of the three cases we consider
here.
Notice
that in each case, we will restrict our analysis to harmonic excitation. For
example, the external force applied to the first system is given by
The
force varies harmonically, with amplitude and frequency .
Similarly, the base motion for the second system is
and
the distance between the small mass and the large mass m for the third system has the same form.
We assume that at time t=0, the initial position and velocity
of each system is
In
each case, we wish to calculate the displacement of the mass x from its static equilibrium
configuration, as a function of time t.
It is of particular interest to determine the influence of forcing amplitude and
frequency on the motion of the mass.
We follow the same approach
to analyze each system: we set up, and solve the equation of motion.
5.4.1 Equations of Motion for Forced Spring
Mass Systems
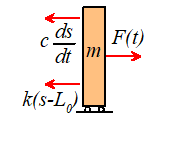
Equation of Motion for External Forcing
We have no problem setting
up and solving equations of motion by now.
First draw a free body diagram for the system, as show on the right
Newton’s
law of motion gives
Rearrange and susbstitute
for F(t)
Check out our list of
solutions to standard ODEs. We find that
if we set
,
our equation can be reduced
to the form
which is on the list.
The (horrible) solution to
this equation is given in the list of solutions. We will discuss the solution later, after we
have analyzed the other two systems.
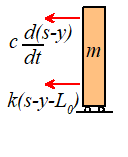 Equation of
Motion for Base Excitation
Equation of
Motion for Base Excitation
Exactly
the same approach works for this system.
The free body diagram is shown in the figure. Note that the
force in the spring is now k(x-y) because
the length of the spring is . Similarly, the rate of change of length
of the dashpot is d(x-y)/dt.
Newton’s
second law then tells us that
Make the
following substitutions
and the equation reduces to
the standard form
Given the initial
conditions
and the base motion
we can look up the solution
in our handy list of solutions to ODEs.
Equation of motion for Rotor Excitation
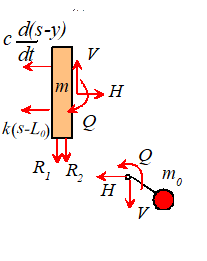
Finally, we will derive the
equation of motion for the third case.
Free body diagrams are shown in the figure for
both the rotor and the mass
Note that the horizontal
acceleration of the mass is
Hence, applying Newton’s second law in the horizontal
direction for both masses:
Add these two equations to
eliminate H and rearrange
To arrange this into
standard form, make the following substitutions
whereupon the equation of
motion reduces to
Finally, look at the
picture to convince yourself that if the crank rotates with angular velocity ,
then
where is the length of the crank.
The solution can once again
be found in the list of solutions to ODEs.
5.4.2 Definition of Transient and Steady
State Response.
If you have
looked at the list of solutions to the equations of motion we derived in the
preceding section, you will have discovered that they look horrible. Unless you have a great deal of experience
with visualizing equations, it is extremely difficult to work out what the
equations are telling us.
If
you have Java, Internet Explorer (or a browser plugin that allows you to run IE
in another browser) you can run a Java Applet to visualize the motion. You can find instructions for installing
Java, the IE plugins, and giving permission for the Applet to run here. The address for the free vibration simulator
(cut and paste this into the Internet Explorer address bar) is
http://www.brown.edu/Departments/Engineering/Courses/En4/java/forced.html
The applet simply
calculates the solution to the equations of motion using the formulae given in
the list of solutions, and plots graphs showing features of the motion. You can use the sliders to set various
parameters in the system, including the type of forcing, its amplitude and
frequency; spring constant, damping coefficient and mass; as well as the position
and velocity of the mass at time t=0. Note that you can control the properties of
the spring-mass system in two ways: you can either set values for k, m
and using the sliders, or you can set ,
K and instead.
We
will use the applet to demonstrate a number of important features of forced
vibrations, including the following:
The steady state response of a forced,
damped, spring mass system is independent of the initial conditions.
To
convince yourself of this, run the applet (click on `start’ and let the system
run for a while). Now, press `stop’;
change the initial position of the mass, and press `start’ again.
You
will see that, after a while, the solution with the new initial conditions is
exactly the same as it was before.
Change the type of forcing, and repeat this test. You can change the initial velocity too, if
you wish.
We
call the behavior of the system as time gets very large the `steady state’ response; and as you
see, it is independent of the initial position and velocity of the mass.
The
behavior of the system while it is approaching the steady state is called the `transient’ response. The transient response depends on
everything…
Now,
reduce the damping coefficient and repeat the test. You will find that the system takes longer to
reach steady state. Thus, the length of
time to reach steady state depends on the properties of the system (and also
the initial conditions).
The
observation that the system always settles to a steady state has two important
consequences. Firstly, we rarely know
the initial conditions for a real engineering system (who knows what the
position and velocity of a bridge is at time t=0?) . Now we know this
doesn’t matter the response is not sensitive to the initial
conditions. Secondly, if we aren’t
interested in the transient response, it turns out we can greatly simplify the
horrible solutions to our equations of motion.
When analyzing forced vibrations, we
(almost) always neglect the transient response of the system, and calculate
only the steady state behavior.
If you look at the
solutions to the equations of motion we calculated in the preceding sections,
you will see that each solution has the form
The
term accounts for the transient response, and is
always zero for large time. The second
term gives the steady state response of the system.
Following
standard convention, we will list only the steady state solutions below. You should bear in mind, however, that the
steady state is only part of the solution, and is only valid if the time is
large enough that the transient term can be neglected.
5.4.3 Summary of Steady-State Response of
Forced Spring Mass Systems.
 This section summarizes all the formulas you will need
to solve problems involving forced vibrations.
This section summarizes all the formulas you will need
to solve problems involving forced vibrations.
Solution for External Forcing
Equation of Motion
with
Steady State Solution:
Here, the function M is called the ‘magnification’ for the
system. M and are graphed below, as a function of
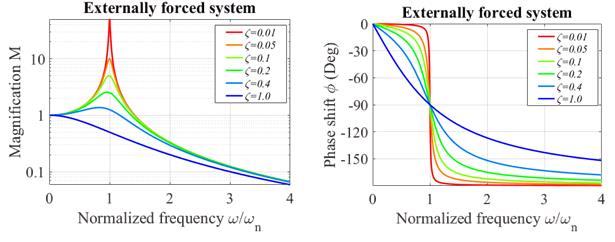
(a)
(b)
Steady state
vibration of a force spring-mass system (a) Magnification (b) phase.
Solution for Base Excitation
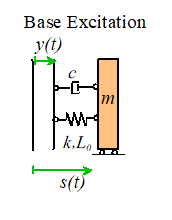
Equation of Motion
with
Steady State solution
The expressions for and are graphed below, as a function of
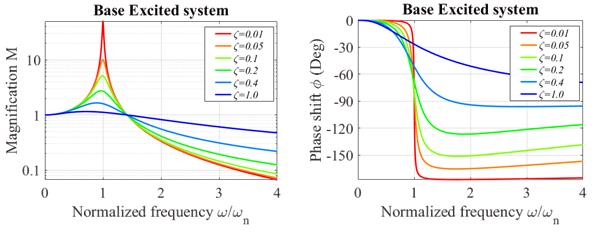
(a)
(b)
Steady state
vibration of a base excited springmass system (a)
Amplitude and (b) phase
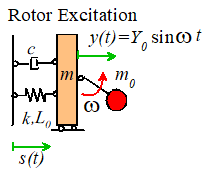 Solution
for Rotor Excitation
Solution
for Rotor Excitation
Equation of Motion
with
Steady state solution
The expressions for and are graphed below, as a function of
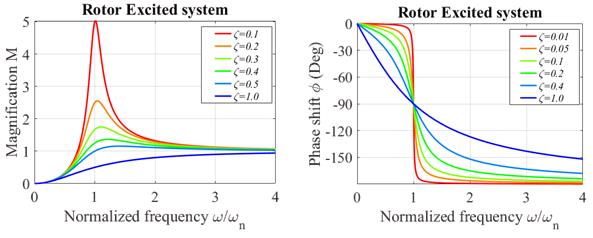
Steady state
vibration of a rotor excited springmass system (a)
Amplitude (b) Phase
5.4.4 Features of the Steady State Response
of Spring Mass Systems to Forced Vibrations.
Now, we will discuss the
implications of the results in the preceding section.
 The
steady state response is always harmonic, and has the same frequency as that of
the forcing.
The
steady state response is always harmonic, and has the same frequency as that of
the forcing.
To see this mathematically, note that
in each case the solution has the form . Recall that defines the frequency of the force, the
frequency of base excitation, or the rotor angular velocity. Thus, the frequency of vibration is
determined by the forcing, not by the properties of the spring-mass
system. This is unlike the free
vibration response.
You can also check this out using our
applet. To switch off the transient
solution, click on the checkbox labeled `show transient’. Then, try running the applet with different values
for k, m and ,
as well as different forcing frequencies, to see what happens. As long as you have switched off the
transient solution, the response will always be harmonic.
 The amplitude of vibration is
strongly dependent on the frequency of excitation, and on the properties of the
springmass system.
The amplitude of vibration is
strongly dependent on the frequency of excitation, and on the properties of the
springmass system.
To see this mathematically, note that
the solution has the form . Observe that is the amplitude of vibration, and look at the
preceding section to find out how the amplitude of vibration varies with
frequency, the natural frequency of the system, the damping factor, and the
amplitude of the forcing. The formulae
for are quite complicated, but you will learn a
great deal if you are able to sketch graphs of as a function of for various values of .
You can also use our applet to study
the influence of forcing frequency, the natural frequency of the system, and the damping coefficient. If you plot position-v-time curves, make sure
you switch off the transient solution to show clearly the steady state
behavior. Note also that if you click on
the `amplitude v- frequency’
radio button just below the graphs, you will see a graph showing the steady
state amplitude of vibration as a function of forcing frequency. The current frequency of excitation is marked
as a square dot on the curve (if you don’t see the square dot, it means the
frequency of excitation is too high to fit on the scale if you lower the excitation frequency and
press `start’ again you should see the dot appear). You can change the properties of the spring
mass system (or the natural frequency and damping coefficient) and draw new
amplitude-v-frequency curves to see how the response of the system has
changed.
Try the following tests
(i) Keeping the natural frequency
fixed (or k and m fixed), plot ampltude-v-frequency graphs for various values of damping
coefficient (or the dashpot coefficient).
What happens to the maximum amplitude of vibration as damping is
reduced?
(ii) Keep the damping coefficient
fixed at around 0.1. Plot graphs of
amplitude-v-frequency for various values of the natural frequency of the
system. How does the maximum vibration
amplitude change as natural frequency is varied? What about the frequency at which the maximum
occurs?
(iii) Keep the dashpot coefficient
fixed at a lowish value. Plot graphs of
amplitude-v-frequency for various values of spring stiffness and mass. Can you reconcile the behavior you observe
with the results of test (ii)?
(iv) Try changing the type of forcing
to base excitation and rotor excitation.
Can you see any differences in the amplitude-v-frequency curves for
different types of forcing?
(v) Set the damping coefficient to a
low value (below 0.1). Keep the natural
frequency fixed. Run the program for
different excitation frequencies. Watch
what the system is doing. Observe the
behavior when the excitation frequency coincides with the natural frequency of
the system. Try this test for each type
of excitation.
 If the forcing
frequency is close to the natural frequency of the system, and the system is
lightly damped, huge vibration amplitudes may occur. This phenomenon is known as resonance.
If the forcing
frequency is close to the natural frequency of the system, and the system is
lightly damped, huge vibration amplitudes may occur. This phenomenon is known as resonance.
If
you ran the tests in the preceding section, you will have seen the system
resonate. Note that the system resonates
at a very similar frequency for each type of forcing.
As a general rule, engineers try to
avoid resonance like the plague.
Resonance is bad vibrations.
Large amplitude vibrations imply large forces; and large forces cause
material failure. There are exceptions
to this rule, of course. Musical
instruments, for example, are supposed to resonate, so as to amplify sound. Musicians who play string, wind and brass
instruments spend years training their lips or bowing arm to excite just the
right vibration modes in their instruments to make them sound perfect. Resonance is a good thing in energy
harvesting systems, and many instruments, such as MEMS gyroscopes, and atomic
force microscopes, work by measuring how an external stimulus of some sort
(rotation, or a surface force) changes the resonant frequency of a system.
 There is a phase lag between the
forcing and the system response, which depends on the frequency of excitation
and the properties of the spring-mass system.
There is a phase lag between the
forcing and the system response, which depends on the frequency of excitation
and the properties of the spring-mass system.
The response of the system is . Expressions for are given in the preceding section. Note that the phase lag is always
negative.
You can use the applet to examine the
physical significance of the phase lag.
Note that you can have the program plot a graph of phase-v-frequency for
you, if you wish.
It is rather unusual to be particularly interested in the
phase of the vibration, so we will not discuss it in detail here.
5.4.5 Engineering implications of vibration behavior
The solutions listed in the
preceding sections give us general guidelines for engineering a system to avoid
(or create!) vibrations.
 Preventing a
system from vibrating: Suppose that
we need to stop a structure or component from vibrating e.g. to stop a tall building from
swaying. Structures are always
deformable to some extent this is represented qualitatively by the
spring in a spring-mass system. They
always have mass this is represented by the mass of the
block. Finally, the damper represents
energy dissipation. Forces acting on a
system generally fluctuate with time.
They probably aren’t perfectly harmonic, but they usually do have a
fairly well defined frequency (visualize waves on the ocean, for example, or
wind gusts. Many vibrations are
man-made, in which case their frequency is known for example vehicles traveling on a road tend
to induce vibrations with a frequency of about 2Hz, corresponding to the bounce
of the car on its suspension).
Preventing a
system from vibrating: Suppose that
we need to stop a structure or component from vibrating e.g. to stop a tall building from
swaying. Structures are always
deformable to some extent this is represented qualitatively by the
spring in a spring-mass system. They
always have mass this is represented by the mass of the
block. Finally, the damper represents
energy dissipation. Forces acting on a
system generally fluctuate with time.
They probably aren’t perfectly harmonic, but they usually do have a
fairly well defined frequency (visualize waves on the ocean, for example, or
wind gusts. Many vibrations are
man-made, in which case their frequency is known for example vehicles traveling on a road tend
to induce vibrations with a frequency of about 2Hz, corresponding to the bounce
of the car on its suspension).
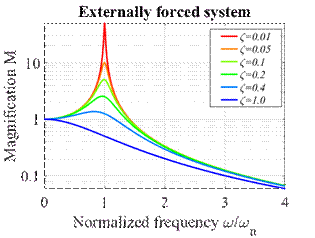
So
how do we stop the system from vibrating?
We know that its motion is given by
To
minimize vibrations, we must design the system to make the vibration amplitude as small as possible. The formula for is a bit scary, which is why we plot graphs of
the solution. The graphs show that we
will observe vibrations with large amplitudes if (i) The frequency is close to 1; and (ii) the damping is small.
At first sight, it looks like we could minimize vibrations by making very large.
This is true in principle, and can be done in some designs, e.g. if the
force acts on a very localized area of the structure, and will only excite a
single vibration mode. For most systems,
this approach will not work, however.
This is because real components generally have a very large number of
natural frequencies of vibration, corresponding to different vibration
modes. We could design the system so
that is large for the mode with the lowest
frequency and perhaps some others but there will always be other modes with
higher frequencies, which will have smaller values of . There
is a risk that one of these will be close to resonance. Consequently, we generally design the system
so that for the mode with the lowest natural
frequency. In fact, design codes usually
specify the minimum allowable value of for vibration critical components. This will guarantee that for all modes, and hence the vibration
amplitude . This tells us that the best approach to avoid
vibrations is to make the structure as stiff as possible. This will make the natural frequency large,
and will also make small.
 Designing a suspension or vibration isolation system. Suspensions, and vibration isolation systems,
are examples of base excited systems. In
this case, the system really consists of a mass (the vehicle, or the isolation
table) on a spring (the shock absorber or vibration isolation pad). We expect that the base will vibrate with some
characteristic frequency .
Our goal is to design the system to minimize the vibration of the mass.
Designing a suspension or vibration isolation system. Suspensions, and vibration isolation systems,
are examples of base excited systems. In
this case, the system really consists of a mass (the vehicle, or the isolation
table) on a spring (the shock absorber or vibration isolation pad). We expect that the base will vibrate with some
characteristic frequency .
Our goal is to design the system to minimize the vibration of the mass.
Our vibration solution
predicts that the mass vibrates with displacement
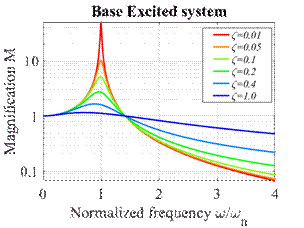
Again,
the graph is helpful to understand how the vibration amplitude varies with system parameters.
Clearly,
we can minimize the vibration amplitude of the mass by making . We can do this by making the spring
stiffness as small as possible (use a soft spring), and making the mass
large. It also helps to make the damping
small.
This is counter-intuitive people often think that the energy dissipated
by the shock absorbers in their suspensions that makes them work. There
are some disadvantages to making the damping too small, however. For one thing, if the system is lightly
damped, and is disturbed somehow, the subsequent transient vibrations will take
a very long time to die out. In
addition, there is always a risk that the frequency of base excitation is lower
than we expect if the system is lightly damped, a potentially
damaging resonance may occur.
Suspension
design involves a bit more than simply minimizing the vibration of the mass, of
course the car will handle poorly if the wheels begin
to leave the ground. A very soft
suspension generally has poor handling, so the engineers must trade off
handling against vibration isolation.
5.4.6 Using Forced Vibration Response to
Measure Properties of a System.
We
often measure the natural frequency and damping coefficient for a mode of
vibration in a structure or component, by measuring the forced vibration
response of the system.
Here
is how this is done. We find some way to
apply a harmonic excitation to the system (base excitation might work; or you
can apply a force using some kind of actuator, or you could deliberately mount
an unbalanced rotor on the system).
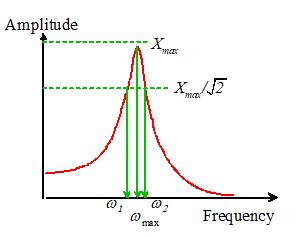
Then,
we mount accelerometers on our system, and use them to measure the displacement
of the structure, at the point where it is being excited, as a function of
frequency.
We
then plot a graph, which usually looks something like the picture on the right.
We read off the maximum response ,
and draw a horizontal line at amplitude . Finally, we measure the frequencies ,
and as shown in the picture.
We define the bandwidth of the response as
Like
the logarithmic decrement, the bandwidth of the forced harmonic response is a
measure of the damping in a system.
It
turns out that we can estimate the natural frequency of the system and its
damping coefficient using the following formulae
The formulae are accurate
for small - say .
To
understand the origin of these formulae, recall that the amplitude of vibration
due to external forcing is given by
We
can find the frequency at which the amplitude is a maximum by differentiating
with respect to ,
setting the derivative equal to zero and solving the resulting equation for
frequency. It turns out that the maximum
amplitude occurs at a frequency
For small ,
we see that
Next,
to get an expression relating the bandwidth to ,
we first calculate the frequencies and . Note that the maximum amplitude of vibration
can be calculated by setting ,
which gives
Now, at the two frequencies
of interest, we know ,
so that and must be solutions of the equation
Rearrange this equation to
see that
This is a quadratic
equation for and has solutions
Expand both expressions in
a Taylor series about to see that
so, finally, we confirm
that
 5.4.7 Example Problems in Forced Vibrations
5.4.7 Example Problems in Forced Vibrations
Example 1: A structure is idealized as a damped springmass system with
stiffness 10 kN/m; mass 2Mg; and dashpot coefficient 2 kNs/m. It is subjected to a harmonic force of
amplitude 500N at frequency 0.5Hz. Calculate
the steady state amplitude of vibration.
Start by calculating the
properties of the system:
Now, the list of solutions
to forced vibration problems gives
For the present problem:
Substituting numbers into
the expression for the vibration amplitude shows that
Example 2: A
car and its suspension system are idealized as a damped springmass system, with
natural frequency 0.5Hz and damping coefficient 0.2. Suppose the car drives at speed V over a road with sinusoidal
roughness. Assume the roughness
wavelength is 10m, and its amplitude is 20cm.
At what speed does the maximum amplitude of vibration occur, and what is
the corresponding vibration amplitude?
Let s denote the distance traveled by the car, and let L denote the wavelength of the roughness
and H the roughness amplitude. Then, the height of the wheel above the mean
road height may be expressed as
Noting that ,
we have that
i.e., the wheel oscillates
vertically with harmonic motion, at frequency .
Now, the suspension has
been idealized as a springmass system
subjected to base excitation. The steady
state vibration is
For light damping, the
maximum amplitude of vibration occurs at around the natural frequency. Therefore, the critical speed follows from
Note that K=1 for base excitation, so that the
amplitude of vibration at is approximately
Note that at this speed,
the suspension system is making the vibration worse. The amplitude of the car’s vibration is
greater than the roughness of the road.
Suspensions work best if they are excited at frequencies well above
their resonant frequencies.
Example 3: The suspension system discussed in the preceding
problem has the following specifications.
For the roadway described in the preceding section, the amplitude of
vibration may not exceed 35cm at any speed.
At 55 miles per hour, the amplitude of vibration must be less than
10cm. The car weighs 3000lb. Select values for the spring stiffness and
the dashpot coefficient.
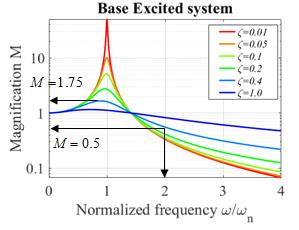
We
must first determine values for and that will satisfy the design specifications.
To this end:
(i)
The specification
requires that
for any value of (remember ). Recall
that and that K=1
for a base excited springmass system. This
tells us that the magnification has to be below 1.75 for any frequency. The
graph shows that if ,
the magnification never exceeds 1.75. We
also see that smaller values of make the suspension more effective (M is smaller) at high frequencies. So is a good choice.
If you prefer not to use the graph, you can use the
approximation which suggests that which gives - but the approximation is not very accurate
for such large values of (to get a better estimate you’d have to
maximize the formula for magnification with respect to but that’s very messy).
(ii)
Now, the
frequency of base excitation at 55mph is
We must choose system parameters so that, at this
excitation frequency, .
This tells us that M
must be less than when is 15.45 rad/s or greater. We already know that ,
and following the curve for this value of we see that M<1/2 if .
Therefore, we must pick .
Again, if you prefer not to use the graph, you can
also solve
for , but this is a pain, and the graph is
accurate enough for a design estimate.
Finally,
we can compute properties of the system.
We have that
Similarly
5.5 Solving differential equations for vibrating systems
Our
goal in this course is to understand what the solutions to differential
equations tell us about engineering problems we might need to solve. But if you have time on your hands, you
might be interested in learning how to solve the differential equations. It’s
fairly straightforward, if a little tedious algebraically. You will learn this material in future
courses (applied math, and several more advanced engineering courses) whether
you want to or not…
Review of complex numbers
It’s
easiest to solve linear ODEs using complex variables. The following definitions and results are
particularly useful:
 Define
Define
 Any complex number z can be split into imaginary and real parts as
Any complex number z can be split into imaginary and real parts as
where
a and b are two real numbers.
 Define the complex conjugate as
Define the complex conjugate as
 It follows that
It follows that
 The exponential of an imaginary number
(Euler’s formula) is
The exponential of an imaginary number
(Euler’s formula) is
You
can prove this by taking the Taylor expansion of both sides of the formula
 Euler’s formula enables us to write any
complex number in polar form
Euler’s formula enables us to write any
complex number in polar form
 Euler’s formula also allows us to represent
trig functions as complex exponentials
Euler’s formula also allows us to represent
trig functions as complex exponentials
 Note that
Note that
Solution to the equation of motion for
an undamped harmonic oscillator
Solve with initial conditions
Guess
a solution of the form where A and
are two complex numbers to be determined (this may seem a cheat, but actually there
are only two ways to do an integral (1) guess a solution, differentiate it, and
see if the answer is correct; and (2) rearrange the integral into another form
with a known solution. We know an
exponential is a good guess for x
because when an exponential is differentiated it stays an exponential). Substitute this into our ODE
We
can satisfy this for any A by
choosing . This
gives us two families of solutions to the equations, one with and another with . The most general solution is the sum of
these, with different coefficients
We need to find :
we can do this by substituting t=0
into x and using the given values of x at t=0
Add and subtract these two
equations to see that
We can use Euler’s formula
to re-write this as
(to see this just
substitute into the formulas and use Euler’s formula to
show are correct).
Finally substitute into the general solution for x to see that
This agrees with the answer
on the formula sheet.
Solution to the equation of motion for a
free damped system
Solve with initial conditions
As before we guess a solution where A and
are two complex numbers to be determined. Substituting into the equation:
This gives a quadratic
equation for (it is called the ‘characteristic equation’
for the differential equation). It has
solutions
Depending on the value of we find
·
(overdamped) two real values of
·
(critical damping):
·
(underdamped) two complex values of
where we have defined To write the answers in terms of real valued
functions we need to treat these cases separately.
Overdamped solution: We have that
We can use the initial
conditions to determine :
Hence
Critically damped solution: our guess for the critically damped solution gives
only which cannot satisfy the initial conditions on
both x and dx/dt, so the solution is incomplete. We have to look around for another solution it turns out that
will
also satisfy the differential equation (this is a standard trick in situations
where the characteristic equation has repeated roots). We can solve for using the initial conditions:
It follows that so the solution is
Underdamped solution: For this case
We can use the initial
conditions to determine (which are now complex):
We can substitute this back
into the solution and re-arrange the result
Finally we recognize the
combinations of complex exponentials as trig functions, giving
Solution to the equation of motion for a
system subjected to harmonic external force
Solve
with initial
conditions
It is helpful to replace the
trig function with its equivalent representation in terms of complex
exponentials
We guess a solution of the
form
where are complex numbers to be determined. Substituting into the ODE:
We can satisfy this by setting
The first two equations show
that
(we introduced M and to re-write in polar form). Finally substitute back for into the guess for and simplify the solution to see that
Finally, we must
determine . By
construction, our guess for satisfies
This is identical to the
differential equation for a damped free vibrating system (but with modified
initial conditions), and we can just write down the solution from the preceding
section.
Short-cut for calculating steady-state solutions for
forced vibrating systems
For example, consider the
base excited system
We anticipate that the
steady-state solution will have the form
so we only need to determine
the magnification and the phase . We
can do this quickly by
(i) Replacing the harmonic function by a complex exponential
(ii) Substituting into the solution
This gives
Hence
Finally, write the complex
numbers on the right hand side in polar form and read off M and
Similarly, to find the
magnification and phase for the rotor-excited system, which has differential
equation
we make the substitutions (i)
and (ii) above and simplify the result to see that:
Re-write the right hand side
in polar form
You
will learn even faster tricks for solving differential equations in circuits
next semester, and perhaps in more advanced level linear systems and control
theory courses. In fact, the pros know
tricks that avoid writing down the differential equation altogether they can just go straight to the
solution! If you want to develop these
superpowers, stick with engineering, and keep writing those generous tuition
checks!
5.6 Introduction to vibration of systems with many degrees of freedom
The
simple 1DOF systems analyzed in the preceding section are very helpful to
develop a feel for the general characteristics of vibrating systems. They are too simple to approximate most real
systems, however. Real systems have
more than just one degree of freedom.
Real systems are also very rarely linear. You may be feeling cheated are the simple idealizations that you get to
see in intro courses really any use? It
turns out that they are, but you can only really be convinced of this if you
know how to analyze more realistic problems, and see that they often behave
just like the simple idealizations.
The
motion of systems with many degrees of freedom, or nonlinear systems, cannot
usually be described using simple formulas. Even when they can, the formulas
are so long and complicated that you need a computer to evaluate them. For this reason, introductory courses
typically avoid these topics. However, if
you are willing to use a computer, analyzing the motion of these complex
systems is actually quite straightforward in fact, often easier than using the nasty
formulas we derived for 1DOF systems.
This
section of the notes is intended mostly for advanced students, who may be
insulted by simplified models. If you
are feeling insulted, read on…
5.6.1 Equations of motion for undamped
linear systems with many degrees of freedom.
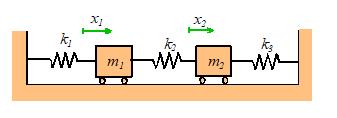 We always express the equations of motion for a system
with many degrees of freedom in a standard form. The two degree of freedom system shown in the
picture can be used as an example. We
won’t go through the calculation in detail here (you should be able to derive
it for yourself draw a FBD, use Newton’s law and all that
tedious stuff), but here is the final answer:
We always express the equations of motion for a system
with many degrees of freedom in a standard form. The two degree of freedom system shown in the
picture can be used as an example. We
won’t go through the calculation in detail here (you should be able to derive
it for yourself draw a FBD, use Newton’s law and all that
tedious stuff), but here is the final answer:
To
solve vibration problems, we always write the equations of motion in matrix
form. For an undamped system, the matrix
equation of motion always looks like this
where
x is a vector of the variables
describing the motion, M is
called the ‘mass matrix’ and K is called
the ‘Stiffness matrix’ for the system.
For the two spring-mass example, the equation of motion can be written
in matrix form as
For
a system with two masses (or more generally, two degrees of freedom), M and K are 2x2 matrices. For a
system with n degrees of freedom,
they are nxn matrices.
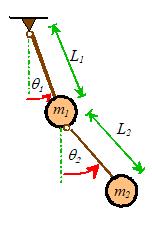 The spring-mass system is linear. A nonlinear system has more complicated
equations of motion, but these can always be arranged into the standard matrix
form by assuming that the displacement of the system is small, and linearizing
the equation of motion. For example, the
full nonlinear equations of motion for the double pendulum shown in the figure
are
The spring-mass system is linear. A nonlinear system has more complicated
equations of motion, but these can always be arranged into the standard matrix
form by assuming that the displacement of the system is small, and linearizing
the equation of motion. For example, the
full nonlinear equations of motion for the double pendulum shown in the figure
are
Here,
a single dot over a variable represents a time derivative, and a double dot
represents a second time derivative (i.e. acceleration). These equations look
horrible (and indeed they are the motion of a double pendulum can even be
chaotic), but if we assume that if ,
,
and their time derivatives are all small, so that terms involving squares, or
products, of these variables can all be neglected, that and recall that and for small x,
the equations simplify to
Or, in matrix form
This is again in the
standard form.
Throughout
the rest of this section, we will focus on exploring the behavior of systems of
springs and masses. This is not because
spring/mass systems are of any particular interest, but because they are easy
to visualize, and, more importantly the equations of motion for a spring-mass
system are identical to those of any linear system. This could include a realistic mechanical system,
an electrical system, or anything that catches your fancy. (Then again, your fancy may tend more towards
nonlinear systems, but if so, you should keep that to yourself).
5.6.2 Natural frequencies and mode
shapes for undamped linear systems with many degrees of freedom.
First,
let’s review the definition of natural frequencies and mode shapes. Recall that
we can set a system vibrating by displacing it slightly from its static
equilibrium position, and then releasing it.
In general, the resulting motion will not be harmonic. However, there are certain special initial
displacements that will cause harmonic vibrations. These special initial deflections are called
mode shapes, and the corresponding frequencies of vibration are called natural
frequencies.
The
natural frequencies of a vibrating system are its most important property. It is helpful to have a simple way to
calculate them.
Fortunately, calculating
natural frequencies turns out to be quite easy (at least on a computer). Recall that the general form of the equation
of motion for a vibrating system is
where x is a time dependent vector that describes the motion, and M and K are mass and stiffness matrices. Since we are interested in
finding harmonic solutions for x, we
can simply assume that the solution has the form ,
and substitute into the equation of motion
The
vectors u and scalars that satisfy a matrix equation of the form are called ‘generalized eigenvectors’ and
‘generalized eigenvalues’ of the equation.
It is impossible to find exact formulas for and u
for a large matrix (formulas exist for up to 5x5 matrices, but they are so
messy they are useless), but MATLAB has built-in functions that will compute
generalized eigenvectors and eigenvalues given numerical values for M and K.
The
special values of satisfying are related to the natural frequencies by
The
special vectors X are the ‘Mode
shapes’ of the system. These are the
special initial displacements that will cause the mass to vibrate
harmonically.
If
you only want to know the natural frequencies (common) you can use the MATLAB
command
d = eig(K,M)
This
returns a vector d, containing all the values of satisfying (for an nxn matrix, there are usually n different values). The natural frequencies follow as .
If
you want to find both the eigenvalues and eigenvectors, you must use
[V,D] = eig(K,M)
This
returns two matrices, V and D. Each column of the matrix V corresponds to a
vector u that satisfies the
equation, and the diagonal elements of D contain the corresponding value of . To extract the ith frequency and mode shape,
use
omega = sqrt(D(i,i))
X = V(:,i)
For
example, here is a MATLAB function that uses this function to automatically
compute the natural frequencies of the spring-mass system shown in the figure.
function [freqs,modes] = compute_frequencies(k1,k2,k3,m1,m2)
M = [m1,0;0,m2];
K = [k1+k2,-k2;-k2,k2+k3];
[V,D] = eig(K,M);
for i = 1:2
freqs(i) = sqrt(D(i,i));
end
modes = V;
end
You could try running this
with
>> [freqs,modes] = compute_frequencies(2,1,1,1,1)
This
gives the natural frequencies as ,
and the mode shapes as (i.e. both masses displace in the same
direction) and (the two masses displace in opposite
directions.
If
you read textbooks on vibrations, you will find that they may give different
formulas for the natural frequencies and vibration modes. (If you read a lot of
textbooks on vibrations there is probably something seriously wrong with your
social life). This is partly because
solving for and u
is rather complicated (especially if you have to do the calculation by hand), and
partly because this formula hides some subtle mathematical features of the
equations of motion for vibrating systems.
For example, the solutions to are generally complex ( and u
have real and imaginary parts), so it is not obvious that our guess actually satisfies the equation of
motion. It turns out, however, that the
equations of motion for a vibrating system can always be arranged so that M and K are symmetric. In this
case and u are
real, and is always positive or zero. The old fashioned formulas for natural
frequencies and vibration modes show this more clearly. But our approach gives the same answer, and
can also be generalized rather easily to solve damped systems (see Section
5.5.5), whereas the traditional textbook methods cannot.
5.6.3 Free vibration of undamped linear
systems with many degrees of freedom.

As
an example, consider a system with n
identical masses with mass m, connected
by springs with stiffness k, as shown
in the picture. Suppose that at time t=0 the masses are displaced from their
static equilibrium position by distances ,
and have initial speeds . We would like to calculate the motion of each
mass as a function of time.
It
is convenient to represent the initial displacement and velocity as n dimensional vectors u and v, as
,
and . In addition, we must calculate the natural
frequencies and mode shapes ,
i=1..n for the system. The motion can then be calculated using the
following formula
where
Here,
the dot represents an n dimensional
dot product (to evaluate it in matlab, just use the dot() command).
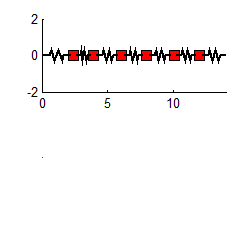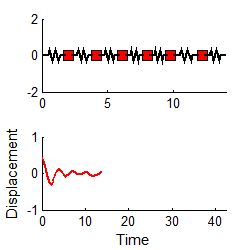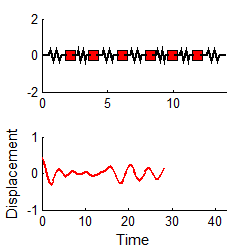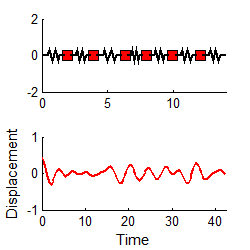
This
expression tells us that the general vibration of the system consists of a sum
of all the vibration modes, (which all vibrate at their own discrete
frequencies). You can control how big
the contribution is from each mode by starting the system with different
initial conditions. The mode shapes have the curious property that the dot
product of two different mode shapes is always zero ( ,
etc) so you can see that if the initial
displacements u happen to be the
same as a mode shape, the vibration will be harmonic.
The
figure on the right animates the motion of a system with 6 masses, which is set
in motion by displacing the leftmost mass and releasing it. The graph shows the displacement of the
leftmost mass as a function of time.
You can download the MATLAB code for this computation here,
and see how the formulas listed in this section are used to compute the motion. The program will predict the motion of a
system with an arbitrary number of masses, and since you can easily edit the
code to type in a different mass and stiffness matrix, it effectively solves any transient vibration problem.
5.6.4 Forced vibration of lightly damped
linear systems with many degrees of freedom.
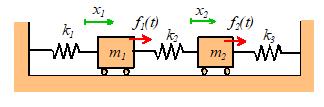
It
is quite simple to find a formula for the motion of an undamped system
subjected to time varying forces. The
predictions are a bit unsatisfactory, however, because their vibration of an
undamped system always depends on the initial conditions. In a real system, damping makes the
steady-state response independent of the initial conditions. However, we can get an approximate solution
for lightly damped systems by finding the solution for an undamped system, and
then neglecting the part of the solution that depends on initial conditions.
As
an example, we will consider the system with two springs and masses shown in
the picture. Each mass is subjected to a
harmonic force, which vibrates with some frequency (the forces acting on the different masses all
vibrate at the same frequency). The equations of motion are
We can write these in
matrix form as
or, more generally,
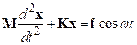
To
find the steady-state solution, we simply assume that the masses will all
vibrate harmonically at the same frequency as the forces. This means that 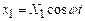 ,
, 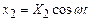 , where
, where 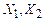 are the (unknown)
amplitudes of vibration of the two masses.
In vector form we could write
are the (unknown)
amplitudes of vibration of the two masses.
In vector form we could write 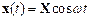 , where
, where 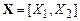 . Substituting this
into the equation of motion gives
. Substituting this
into the equation of motion gives
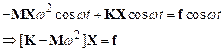
This is a system of linear equations
for X. They can easily be solved using MATLAB. As an example, here is a simple MATLAB
function that will calculate the vibration amplitude for a linear system with
many degrees of freedom, given the stiffness and mass matrices, and the vector
of forces f.
function X = forced_vibration(K,M,f,omega)
% Function to calculate steady state amplitude of
% a forced linear system.
% K is nxn the stiffness matrix
% M is the nxn mass matrix
% f is the n dimensional force vector
% omega is the forcing frequency, in radians/sec.
% The function computes a vector X, giving the amplitude of
% each degree of freedom
%
X = (K-M*omega^2)\f;
end
The function is only one
line long!
As
an example, the graph below shows the predicted steady-state vibration
amplitude for the spring-mass system, for the special case where the masses are
all equal 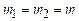 , and the springs all have the same stiffness
, and the springs all have the same stiffness 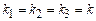 . The first mass is
subjected to a harmonic force
. The first mass is
subjected to a harmonic force 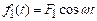 , and no force acts on the second mass. Note that the graph shows the magnitude of
the vibration amplitude the formula predicts that for some frequencies
some masses have negative vibration amplitudes, but the negative sign has been
ignored, as the negative sign just means that the mass vibrates out of phase
with the force.
, and no force acts on the second mass. Note that the graph shows the magnitude of
the vibration amplitude the formula predicts that for some frequencies
some masses have negative vibration amplitudes, but the negative sign has been
ignored, as the negative sign just means that the mass vibrates out of phase
with the force.
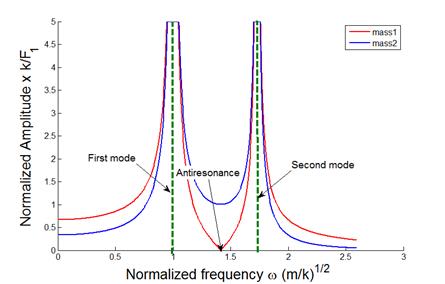
Several
features of the result are worth noting:

 If the forcing frequency is close to
any one of the natural frequencies of the system, huge vibration amplitudes
occur. This phenomenon is known as resonance. You can check the natural frequencies of the
system using the little matlab code in section 5.5.2 they turn out to be
If the forcing frequency is close to
any one of the natural frequencies of the system, huge vibration amplitudes
occur. This phenomenon is known as resonance. You can check the natural frequencies of the
system using the little matlab code in section 5.5.2 they turn out to be 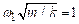 and
and 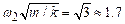 . At these frequencies
the vibration amplitude is theoretically infinite.
. At these frequencies
the vibration amplitude is theoretically infinite.
 The figure predicts an intriguing new
phenomenon at a magic frequency, the amplitude of
vibration of mass 1 (that’s the mass that the force acts on) drops to
zero. This is called ‘Anti-resonance,’
and it has an important engineering application. Suppose that we have designed a system with a
serious vibration problem (like the London Millenium bridge). Usually, this occurs because some kind of
unexpected force is exciting one of the vibration modes in the system. We can idealize this behavior as a
mass-spring system subjected to a force, as shown in the figure. So how do we stop the system from
vibrating? Our solution for a 2DOF
system shows that a system with two masses will have an anti-resonance. So we simply turn our 1DOF system into a 2DOF
system by adding another spring and a mass, and tune the stiffness and mass of
the new elements so that the anti-resonance occurs at the appropriate
frequency. Of course, adding a mass
will create a new vibration mode, but we can make sure that the new natural
frequency is not at a bad frequency. We
can also add a dashpot in parallel with the spring, if we want this has the effect of making the
anti-resonance phenomenon somewhat less effective (the vibration amplitude will
be small, but finite, at the ‘magic’ frequency), but the new vibration modes
will also have lower amplitudes at resonance. The added spring mass system is called a ‘tuned vibration
absorber.’ This approach was used to solve the Millenium Bridge
vibration problem.
The figure predicts an intriguing new
phenomenon at a magic frequency, the amplitude of
vibration of mass 1 (that’s the mass that the force acts on) drops to
zero. This is called ‘Anti-resonance,’
and it has an important engineering application. Suppose that we have designed a system with a
serious vibration problem (like the London Millenium bridge). Usually, this occurs because some kind of
unexpected force is exciting one of the vibration modes in the system. We can idealize this behavior as a
mass-spring system subjected to a force, as shown in the figure. So how do we stop the system from
vibrating? Our solution for a 2DOF
system shows that a system with two masses will have an anti-resonance. So we simply turn our 1DOF system into a 2DOF
system by adding another spring and a mass, and tune the stiffness and mass of
the new elements so that the anti-resonance occurs at the appropriate
frequency. Of course, adding a mass
will create a new vibration mode, but we can make sure that the new natural
frequency is not at a bad frequency. We
can also add a dashpot in parallel with the spring, if we want this has the effect of making the
anti-resonance phenomenon somewhat less effective (the vibration amplitude will
be small, but finite, at the ‘magic’ frequency), but the new vibration modes
will also have lower amplitudes at resonance. The added spring mass system is called a ‘tuned vibration
absorber.’ This approach was used to solve the Millenium Bridge
vibration problem.
5.6.5 The effects of damping
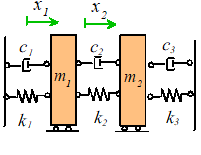 In most design calculations, we don’t worry about
accounting for the effects of damping very accurately. This is partly because it’s very difficult to
find formulas that model damping realistically, and even more difficult to find
values for the damping parameters.
Also, the mathematics required to solve damped problems is a bit messy.
Old textbooks don’t cover it, because for practical purposes it is only
possible to do the calculations using a computer. It is not hard to account for the effects of
damping, however, and it is helpful to have a sense of what its effect will be
in a real system. We’ll go through this
rather briefly in this section.
In most design calculations, we don’t worry about
accounting for the effects of damping very accurately. This is partly because it’s very difficult to
find formulas that model damping realistically, and even more difficult to find
values for the damping parameters.
Also, the mathematics required to solve damped problems is a bit messy.
Old textbooks don’t cover it, because for practical purposes it is only
possible to do the calculations using a computer. It is not hard to account for the effects of
damping, however, and it is helpful to have a sense of what its effect will be
in a real system. We’ll go through this
rather briefly in this section.
Equations of motion: The figure shows a damped spring-mass system. The equations of motion for the system can
easily be shown to be
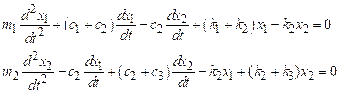
To
solve these equations, we have to reduce them to a system that MATLAB can
handle, by re-writing them as first order equations. We follow the standard procedure to do this define 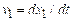 and
and 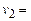
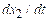 as new variables, and
then write the equations in matrix form as
as new variables, and
then write the equations in matrix form as
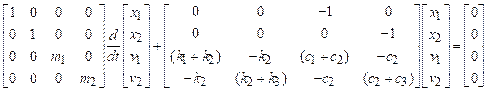
(This result might not be
obvious to you if so, multiply out the vector-matrix products
to see that the equations are all correct). This is a matrix equation of the
form
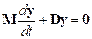
where y is a vector containing the unknown velocities and positions of
the mass.
Free vibration response: Suppose that at time t=0 the system has initial positions and velocities 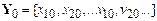 , and we wish to calculate the subsequent motion of the
system. To do this, we must solve the equation of motion. We start by guessing
that the solution has the form
, and we wish to calculate the subsequent motion of the
system. To do this, we must solve the equation of motion. We start by guessing
that the solution has the form 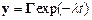 (the negative sign is
introduced because we expect solutions to decay with time). Here,
(the negative sign is
introduced because we expect solutions to decay with time). Here, 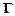 is a constant vector,
to be determined. Substituting this
into the equation of motion gives
is a constant vector,
to be determined. Substituting this
into the equation of motion gives
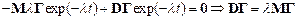
This
is another generalized eigenvalue problem, and can easily be solved with
MATLAB. The solution is much more
complicated for a damped system, however, because the possible values of  and
and  that satisfy the
equation are in general complex that is to say, each
that satisfy the
equation are in general complex that is to say, each  can be expressed as
can be expressed as 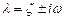 , where
, where  and
and  are positive real numbers, and
are positive real numbers, and 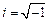 . This makes more
sense if we recall Euler’s formula
. This makes more
sense if we recall Euler’s formula
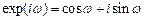
(if
you haven’t seen Euler’s formula, try doing a Taylor expansion of both sides of
the equation you will find they are magically equal. If you don’t know how to do a Taylor
expansion, you probably stopped reading this ages ago, but if you are still
hanging in there, just trust me…). So,
the solution is predicting that the response may be oscillatory, as we would
expect. Once all the possible vectors  and
and  have been calculated,
the response of the system can be calculated as follows:
have been calculated,
the response of the system can be calculated as follows:
1.
Construct a
matrix H , in which each column is
one of the possible values of  (MATLAB constructs
this matrix automatically)
(MATLAB constructs
this matrix automatically)
2. Construct a diagonal matrix  (t), which has the form
(t), which has the form
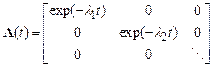
where
each  is one of the
solutions to the generalized eigenvalue equation.
is one of the
solutions to the generalized eigenvalue equation.
3. Calculate a vector a (this represents the amplitudes of the various modes in the
vibration response) that satisfies
4. The vibration response then follows as
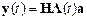
All
the matrices and vectors in these formulas are complex valued but all the imaginary parts magically
disappear in the final answer.
 HEALTH
WARNING: The formulas listed here
only work if all the generalized eigenvalues
HEALTH
WARNING: The formulas listed here
only work if all the generalized eigenvalues 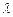 satisfying
satisfying 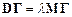 are different. For
some very special choices of damping, some eigenvalues may be repeated. In this case the formula won’t work. A quick and dirty fix for this is just to
change the damping very slightly, and the problem disappears. Your applied math courses will hopefully
show you a better fix, but we won’t worry about that here.
are different. For
some very special choices of damping, some eigenvalues may be repeated. In this case the formula won’t work. A quick and dirty fix for this is just to
change the damping very slightly, and the problem disappears. Your applied math courses will hopefully
show you a better fix, but we won’t worry about that here.
This
all sounds a bit involved, but it actually only takes a few lines of MATLAB code
to calculate the motion of any damped system. As an example, a MATLAB code that
animates the motion of a damped spring-mass system shown in the figure (but
with an arbitrary number of masses) can be downloaded
here. You can use the code to
explore the behavior of the system. In
addition, you can modify the code to solve any linear free vibration problem by
modifying the matrices M and D.
Here
are some animations that illustrate the behavior of the system. The animations
below show vibrations of the system with initial displacements corresponding to
the three mode shapes of the undamped system (calculated using the procedure in
Section 5.5.2). The results are shown
for k=m=1 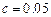 . In each case, the graph plots the motion of the three
masses if a color doesn’t show up, it means one of
the other masses has the exact same displacement.
. In each case, the graph plots the motion of the three
masses if a color doesn’t show up, it means one of
the other masses has the exact same displacement.
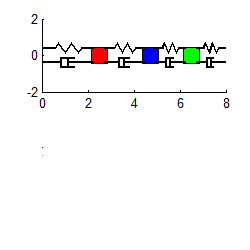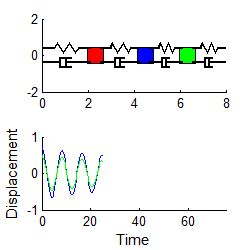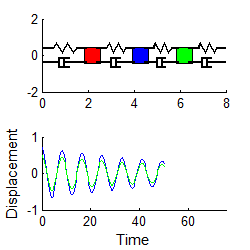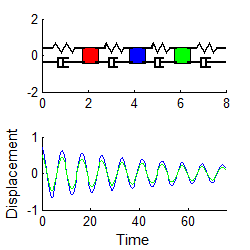
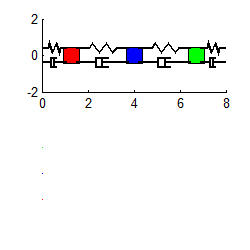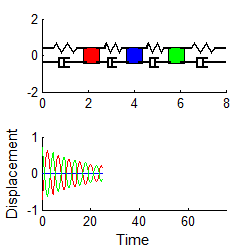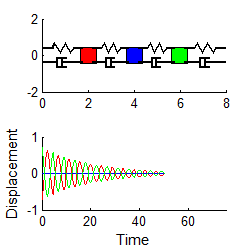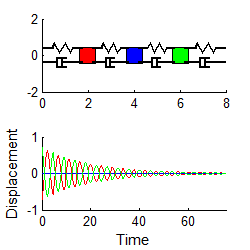
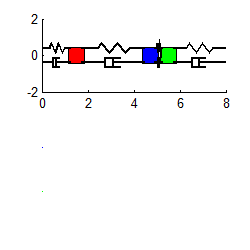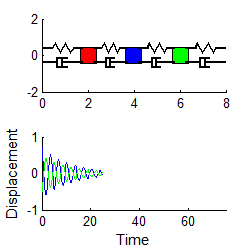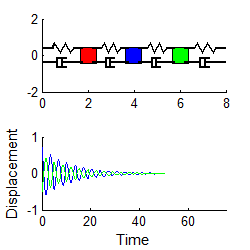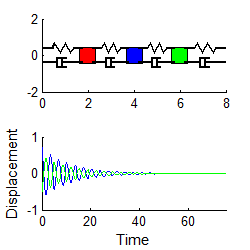
Mode 1 Mode
2
Mode 3
Notice that
1.
For each mode,
the displacement history of any mass looks very similar to the behavior of a damped,
1DOF system.
2. The amplitude of the high frequency modes die out much
faster than the low frequency mode.
 This explains why it is so helpful to understand the
behavior of a 1DOF system. If a more
complicated system is set in motion, its response initially involves
contributions from all its vibration modes.
Soon, however, the high frequency modes die out, and the dominant
behavior is just caused by the lowest frequency mode. The animation to the
right demonstrates this very nicely here, the system was started by displacing
only the first mass. The initial
response is not harmonic, but after a short time the high frequency modes stop
contributing, and the system behaves just like a 1DOF approximation. For design purposes, idealizing the system as
a 1DOF damped spring-mass system is usually sufficient.
This explains why it is so helpful to understand the
behavior of a 1DOF system. If a more
complicated system is set in motion, its response initially involves
contributions from all its vibration modes.
Soon, however, the high frequency modes die out, and the dominant
behavior is just caused by the lowest frequency mode. The animation to the
right demonstrates this very nicely here, the system was started by displacing
only the first mass. The initial
response is not harmonic, but after a short time the high frequency modes stop
contributing, and the system behaves just like a 1DOF approximation. For design purposes, idealizing the system as
a 1DOF damped spring-mass system is usually sufficient.
Notice
also that light damping has very little effect on the natural frequencies and
mode shapes so the simple undamped approximation is a good
way to calculate these.
Of
course, if the system is very heavily damped, then its behavior changes
completely the system no longer vibrates, and instead
just moves gradually towards its equilibrium position. You can simulate this behavior for yourself
using the matlab code try running it with 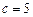 or higher. Systems of this kind are not of much
practical interest.
or higher. Systems of this kind are not of much
practical interest.
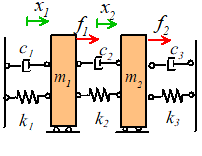
Steady-state forced vibration response. Finally, we
take a look at the effects of damping on the response of a spring-mass system
to harmonic forces. The equations of
motion for a damped, forced system are
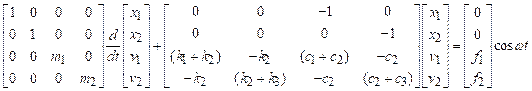
This is an equation of the form
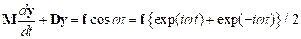
where we have used Euler’s
famous formula again. We can find a
solution to
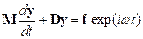
by guessing that 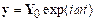 , and substituting into the matrix equation
, and substituting into the matrix equation
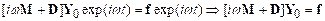
This equation can be solved
for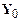 . Similarly, we can
solve
. Similarly, we can
solve
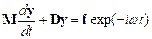
by
guessing that 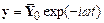 , which gives an equation for
, which gives an equation for 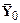 of the form
of the form 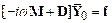 . You actually don’t need to solve this equation you can simply calculate
. You actually don’t need to solve this equation you can simply calculate 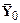 by just changing the
sign of all the imaginary parts of
by just changing the
sign of all the imaginary parts of 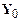 . The full solution follows as
. The full solution follows as
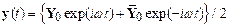
This
is the steady-state vibration response.
Just as for the 1DOF system, the general solution also has a transient
part, which depends on initial conditions. We know that the transient solution
will die away, so we ignore it.
The
solution for y(t) looks peculiar,
because of the complex numbers. If we
just want to plot the solution as a function of time, we don’t have to worry
about the complex numbers, because they magically disappear in the final
answer. In fact, if we use MATLAB to do
the computations, we never even notice that the intermediate formulas involve
complex numbers. If we do plot the
solution, it is obvious that each mass vibrates harmonically, at the same frequency
as the force (this is obvious from the formula too). It’s not worth plotting the function we are really only interested in the amplitude
of vibration of each mass. This can be calculated as follows
1.
Let  ,
, 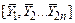 denote the components
of
denote the components
of 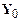 and
and 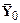
2.
The vibration of
the jth mass then has the form
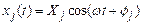
where
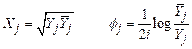
are
the amplitude and phase of the harmonic vibration of the mass.
If
you know a lot about complex numbers you could try to derive these formulas for
yourself. If not, just trust me your math classes should cover this kind of
thing. MATLAB can handle all these
computations effortlessly. As an
example, here is a simple MATLAB script that will calculate the steady-state
amplitude of vibration and phase of each degree of freedom of a forced n degree of freedom system, given the
force vector f, and the matrices M and D that describe the system.
function [amp,phase] = damped_forced_vibration(D,M,f,omega)
% Function to calculate steady state amplitude of
% a forced linear system.
% D is 2nx2n the stiffness/damping matrix
% M is the 2nx2n mass matrix
% f is the 2n dimensional force vector
% omega is the forcing frequency, in radians/sec.
% The function computes a vector ‘amp’, giving the amplitude
of
% each degree of freedom, and a second vector ‘phase’,
% which gives the phase of each degree of freedom
%
Y0 = (D+M*i*omega)\f; % The i
here is sqrt(-1)
% We dont need to calculate Y0bar - we can just change the
sign of
% the imaginary part of Y0 using the 'conj' command
for j =1:length(f)/2
amp(j) =
sqrt(Y0(j)*conj(Y0(j)));
phase(j) =
log(conj(Y0(j))/Y0(j))/(2*i);
end
end
Again, the script is very
simple.
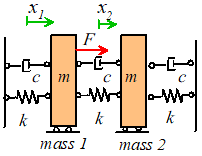
Here is a graph showing the
predicted vibration amplitude of each mass in the system shown. Note that only mass 1 is subjected to a
force.
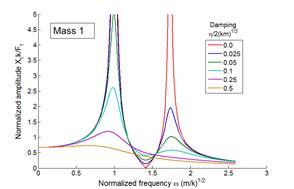
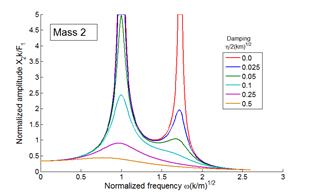
The important conclusions
to be drawn from these results are:
1.
We observe two
resonances, at frequencies very close to the undamped natural frequencies of
the system.
2.
For light
damping, the undamped model predicts the vibration amplitude quite accurately,
except very close to the resonance itself (where the undamped model has an
infinite vibration amplitude)
3.
In a damped
system, the amplitude of the lowest frequency resonance is generally much
greater than higher frequency modes. For
this reason, it is often sufficient to consider only the lowest frequency mode in
design calculations. This means we can
idealize the system as just a single DOF system, and think of it as a simple
spring-mass system as described in the early part of this chapter. The relative vibration amplitudes of the
various resonances do depend to some extent on the nature of the force it is possible to choose a set of forces that
will excite only a high frequency
mode, in which case the amplitude of this special excited mode will exceed all
the others. But for most forcing, the
lowest frequency one is the one that matters.
4.
The ‘anti-resonance’
behavior shown by the forced mass disappears if the damping is too high.




 Vehicle
suspension systems are familiar to everyone, but continue to evolve as
engineers work to improve vehicle handling and ride (the figure above is from http://www.altairhyperworks.com. A radical
new approach to suspension design emerged in 2003 when a research group led by
Malcolm Smith at Cambridge University invented a new mechanical suspension
element they called an ‘inerter’. This
device can be thought of as a sort of generalized spring, but instead of
exerting a force proportional to the relative displacement of its two ends, the
inerter exerts a force that is proportional to the relative acceleration of its two ends. An actual realization is shown in the
figure. You can find a detailed
presentation on the theory behind the device at http://www-control.eng.cam.ac.uk/~mcs/lecture_j.pdf The device was adopted in secret by the McLaren
Formula 1 racing team in 2005 (they called it the ‘J damper’, and a scandal
erupted in Formula 1 racing when the Renault team managed to steal drawings for
the device, but were unable to work out what it does. The patent for the device has now been
licensed Penske and looks to become a standard element in formula 1
racing. It is only a matter of time
before it appears on vehicles available to the rest of us.
Vehicle
suspension systems are familiar to everyone, but continue to evolve as
engineers work to improve vehicle handling and ride (the figure above is from http://www.altairhyperworks.com. A radical
new approach to suspension design emerged in 2003 when a research group led by
Malcolm Smith at Cambridge University invented a new mechanical suspension
element they called an ‘inerter’. This
device can be thought of as a sort of generalized spring, but instead of
exerting a force proportional to the relative displacement of its two ends, the
inerter exerts a force that is proportional to the relative acceleration of its two ends. An actual realization is shown in the
figure. You can find a detailed
presentation on the theory behind the device at http://www-control.eng.cam.ac.uk/~mcs/lecture_j.pdf The device was adopted in secret by the McLaren
Formula 1 racing team in 2005 (they called it the ‘J damper’, and a scandal
erupted in Formula 1 racing when the Renault team managed to steal drawings for
the device, but were unable to work out what it does. The patent for the device has now been
licensed Penske and looks to become a standard element in formula 1
racing. It is only a matter of time
before it appears on vehicles available to the rest of us. Precision
Machinery: The picture on the right shows one example of a
precision instrument. It is essential
to isolate electron microscopes from vibrations. A typical transmission electron microscope is
designed to resolve features of materials down to atomic length scales. If the specimen vibrates by more than a few
atomic spacings, it will be impossible to see!
This is one reason that electron microscopes are always located in the
basement the basement of a building vibrates much less
than the upper floors. Professor K.-S. Kim at Brown recently invented
and patented a new vibration isolation system to support his atomic force
microscope on the 7th floor of the Barus-Holley building you can find the patent at United
States Patent, Patent Number 7,543,791.
Precision
Machinery: The picture on the right shows one example of a
precision instrument. It is essential
to isolate electron microscopes from vibrations. A typical transmission electron microscope is
designed to resolve features of materials down to atomic length scales. If the specimen vibrates by more than a few
atomic spacings, it will be impossible to see!
This is one reason that electron microscopes are always located in the
basement the basement of a building vibrates much less
than the upper floors. Professor K.-S. Kim at Brown recently invented
and patented a new vibration isolation system to support his atomic force
microscope on the 7th floor of the Barus-Holley building you can find the patent at United
States Patent, Patent Number 7,543,791. The picture shows features of a typical hard disk
drive. It is particularly important to
prevent vibrations in the disk stack assembly and in the disk head positioner,
since any relative motion between these two components will make it impossible
to read data. The spinning disk stack assembly has some very interesting
vibration characteristics (which fortunately for you, is beyond the scope of
this course).
The picture shows features of a typical hard disk
drive. It is particularly important to
prevent vibrations in the disk stack assembly and in the disk head positioner,
since any relative motion between these two components will make it impossible
to read data. The spinning disk stack assembly has some very interesting
vibration characteristics (which fortunately for you, is beyond the scope of
this course). Vibrations are not always undesirable, however. On occasion, they can be put to good
use. Examples of beneficial applications
of vibrations include ultrasonic probes, both for medical application and for
nondestructive testing. The picture shows a
medical application of ultrasound: it is an image of someone’s colon. This type of instrument can resolve features
down to a fraction of a millimeter, and is infinitely preferable to exploratory
surgery. Ultrasound is also used to
detect cracks in aircraft and structures.
Vibrations are not always undesirable, however. On occasion, they can be put to good
use. Examples of beneficial applications
of vibrations include ultrasonic probes, both for medical application and for
nondestructive testing. The picture shows a
medical application of ultrasound: it is an image of someone’s colon. This type of instrument can resolve features
down to a fraction of a millimeter, and is infinitely preferable to exploratory
surgery. Ultrasound is also used to
detect cracks in aircraft and structures. When faced with a vibration problem, engineers
generally start by making some measurements to try to isolate the cause of the
problem. There are two common ways to
measure vibrations:
When faced with a vibration problem, engineers
generally start by making some measurements to try to isolate the cause of the
problem. There are two common ways to
measure vibrations:
![]() The signal is
often (although not always) periodic:
that is to say, it repeats itself at fixed intervals of time. Vibrations that do not repeat themselves in
this way are said to be random. All the systems we consider in this course
will exhibit periodic vibrations.
The signal is
often (although not always) periodic:
that is to say, it repeats itself at fixed intervals of time. Vibrations that do not repeat themselves in
this way are said to be random. All the systems we consider in this course
will exhibit periodic vibrations.![]() The PERIOD of the signal, T, is the time required for
one complete cycle of oscillation, as shown in the picture.
The PERIOD of the signal, T, is the time required for
one complete cycle of oscillation, as shown in the picture.![]() The FREQUENCY of
the signal, f, is the number of cycles of oscillation per
second. Cycles per second is often given the name Hertz: thus, a signal which
repeats 100 times per second is said to oscillate at 100 Hertz.
The FREQUENCY of
the signal, f, is the number of cycles of oscillation per
second. Cycles per second is often given the name Hertz: thus, a signal which
repeats 100 times per second is said to oscillate at 100 Hertz.![]() The ANGULAR
FREQUENCY of the signal, ,
is defined as .
We specify angular frequency in radians per second. Thus, a signal that oscillates at 100 Hz has
angular frequency radians per second.
The ANGULAR
FREQUENCY of the signal, ,
is defined as .
We specify angular frequency in radians per second. Thus, a signal that oscillates at 100 Hz has
angular frequency radians per second. ![]() Period, frequency
and angular frequency are related by
Period, frequency
and angular frequency are related by![]() The PEAK-TO-PEAK
AMPLITUDE of the signal, A, is the difference between its maximum value and
its minimum value, as shown in the picture
The PEAK-TO-PEAK
AMPLITUDE of the signal, A, is the difference between its maximum value and
its minimum value, as shown in the picture![]() The AMPLITUDE
of the signal is generally taken to mean half its peak to peak amplitude.
Engineers sometimes use amplitude as an abbreviation for peak to peak
amplitude, however, so be careful.
The AMPLITUDE
of the signal is generally taken to mean half its peak to peak amplitude.
Engineers sometimes use amplitude as an abbreviation for peak to peak
amplitude, however, so be careful.![]() The ROOT MEAN
SQUARE AMPLITUDE or RMS amplitude is defined as
The ROOT MEAN
SQUARE AMPLITUDE or RMS amplitude is defined as![]() Recall that a
system is conservative if energy is
conserved, i.e. potential energy + kinetic energy = constant during motion.
Recall that a
system is conservative if energy is
conserved, i.e. potential energy + kinetic energy = constant during motion.![]() Free vibration means that no
time varying external forces act on the system.
Free vibration means that no
time varying external forces act on the system.
![]() A system has one degree of freedom if its motion can
be completely described by a single scalar variable. We’ll discuss this in a bit more detail
later.
A system has one degree of freedom if its motion can
be completely described by a single scalar variable. We’ll discuss this in a bit more detail
later.![]() A system is said to be linear if its equation of motion is linear. We will see what this means shortly.
A system is said to be linear if its equation of motion is linear. We will see what this means shortly.

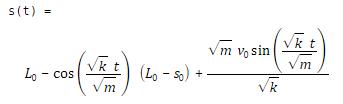
 5.2.2
Solution to the equation of motion for an undamped spring-mass system
5.2.2
Solution to the equation of motion for an undamped spring-mass system![]() The mass
oscillates harmonically, as discussed in the preceding section;
The mass
oscillates harmonically, as discussed in the preceding section;![]() The angular frequency of oscillation, ,
is a characteristic property of the system, and is independent of the initial
position or velocity of the mass. This
is a very important observation, and we will expand upon it below. The characteristic frequency is known as the natural frequency of the system.
The angular frequency of oscillation, ,
is a characteristic property of the system, and is independent of the initial
position or velocity of the mass. This
is a very important observation, and we will expand upon it below. The characteristic frequency is known as the natural frequency of the system.![]() Increasing the stiffness of the spring increases the
natural frequency of the system;
Increasing the stiffness of the spring increases the
natural frequency of the system;![]() Increasing the mass reduces the natural frequency of
the system.
Increasing the mass reduces the natural frequency of
the system. For the springmass system, we
found only one natural frequency. More
complex systems have several natural frequencies. For example, the system of two masses shown
below has two natural frequencies, given by
For the springmass system, we
found only one natural frequency. More
complex systems have several natural frequencies. For example, the system of two masses shown
below has two natural frequencies, given by The response may be shown (see sect 5.5 if you
want to know how) to be
The response may be shown (see sect 5.5 if you
want to know how) to be However, if we
choose the special initial conditions:
However, if we
choose the special initial conditions:


 Thus, except for some rather special initial
conditions, x increases without bound
as time increases. This is a
characteristic of an unstable mechanical
system.
Thus, except for some rather special initial
conditions, x increases without bound
as time increases. This is a
characteristic of an unstable mechanical
system.
 Example 3: A system with
a rigid body (the KE of a rigid body will be defined in the next section of the
course just live with it for now!).
Example 3: A system with
a rigid body (the KE of a rigid body will be defined in the next section of the
course just live with it for now!).

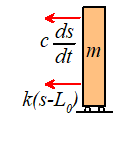
![]() Set the dashpot
coefficient to a low value, so that the damping
coefficient . Make sure the graph is set to display
position versus time, and press `start.’ You should see the system
vibrate. The vibration looks very similar to the
behavior of the conservative system we analyzed in the preceding section,
except that the amplitude decays with time.
Note that the system vibrates at a frequency very slightly lower than
the natural frequency of the system.
Set the dashpot
coefficient to a low value, so that the damping
coefficient . Make sure the graph is set to display
position versus time, and press `start.’ You should see the system
vibrate. The vibration looks very similar to the
behavior of the conservative system we analyzed in the preceding section,
except that the amplitude decays with time.
Note that the system vibrates at a frequency very slightly lower than
the natural frequency of the system.![]() Keeping the value
of fixed, vary the values of spring constant and
mass to see what happens to the frequency of vibration and also to the rate of
decay of vibration. Is the behavior
consistent with the solutions given above?
Keeping the value
of fixed, vary the values of spring constant and
mass to see what happens to the frequency of vibration and also to the rate of
decay of vibration. Is the behavior
consistent with the solutions given above?![]() Keep the values of k and m fixed, and vary . You should see that, as you increase ,
the vibration dies away more and more quickly.
What happens to the frequency of oscillations as is increased?
Is this behavior consistent with the predictions of the theory?
Keep the values of k and m fixed, and vary . You should see that, as you increase ,
the vibration dies away more and more quickly.
What happens to the frequency of oscillations as is increased?
Is this behavior consistent with the predictions of the theory?![]() Now, set the damping coefficient (not the
dashpot coefficient this time) to . For this value, the system no longer
vibrates; instead, the mass smoothly returns to its equilibrium position x=0.
If you need to design a system that returns to its equilibrium position
in the shortest possible time, then it is customary to select system parameters so that . A system of this kind is said to be critically damped.
Now, set the damping coefficient (not the
dashpot coefficient this time) to . For this value, the system no longer
vibrates; instead, the mass smoothly returns to its equilibrium position x=0.
If you need to design a system that returns to its equilibrium position
in the shortest possible time, then it is customary to select system parameters so that . A system of this kind is said to be critically damped.![]() Set to a value greater than 1. Under these conditions, the system decays
more slowly towards its equilibrium configuration.
Set to a value greater than 1. Under these conditions, the system decays
more slowly towards its equilibrium configuration.![]() Keeping >1, experiment with the effects of changing
the stiffness of the spring and the value of the mass. Can you explain what is happening
mathematically, using the equations of motion and their solution?
Keeping >1, experiment with the effects of changing
the stiffness of the spring and the value of the mass. Can you explain what is happening
mathematically, using the equations of motion and their solution?![]() Finally, you might like to look at the
behavior of the system on its phase plane.
In this course, we will not make much use of the phase plane, but it is
a powerful tool for visualizing the behavior of nonlinear systems. By looking at the patterns traced by the
system on the phase plane, you can often work out what it is doing. For example, if the trajectory encircles the
origin, then the system is vibrating. If
the trajectory approaches the origin, the system is decaying to its equilibrium
configuration.
Finally, you might like to look at the
behavior of the system on its phase plane.
In this course, we will not make much use of the phase plane, but it is
a powerful tool for visualizing the behavior of nonlinear systems. By looking at the patterns traced by the
system on the phase plane, you can often work out what it is doing. For example, if the trajectory encircles the
origin, then the system is vibrating. If
the trajectory approaches the origin, the system is decaying to its equilibrium
configuration. 
 Finally, we solve the most important vibration
problems of all. In engineering
practice, we are almost invariably interested in predicting the response of a
structure or mechanical system to external forcing. For example, we may need to predict the
response of a bridge or tall building to wind loading, earthquakes, or ground
vibrations due to traffic. Another
typical problem you are likely to encounter is to isolate a sensitive system
from vibrations. For example, the
suspension of your car is designed to isolate a sensitive system (you) from
bumps in the road. Electron microscopes
are another example of sensitive instruments that must be isolated from
vibrations. Electron microscopes are designed
to resolve features a few nanometers in size.
If the specimen vibrates with amplitude of only a few nanometers, it
will be impossible to see! Great care is
taken to isolate this kind of instrument from vibrations. That is one reason they are almost always in
the basement of a building: the basement vibrates much less than the floors
above.
Finally, we solve the most important vibration
problems of all. In engineering
practice, we are almost invariably interested in predicting the response of a
structure or mechanical system to external forcing. For example, we may need to predict the
response of a bridge or tall building to wind loading, earthquakes, or ground
vibrations due to traffic. Another
typical problem you are likely to encounter is to isolate a sensitive system
from vibrations. For example, the
suspension of your car is designed to isolate a sensitive system (you) from
bumps in the road. Electron microscopes
are another example of sensitive instruments that must be isolated from
vibrations. Electron microscopes are designed
to resolve features a few nanometers in size.
If the specimen vibrates with amplitude of only a few nanometers, it
will be impossible to see! Great care is
taken to isolate this kind of instrument from vibrations. That is one reason they are almost always in
the basement of a building: the basement vibrates much less than the floors
above.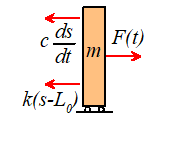
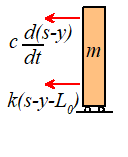 Equation of
Motion for Base Excitation
Equation of
Motion for Base Excitation
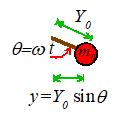
 This section summarizes all the formulas you will need
to solve problems involving forced vibrations.
This section summarizes all the formulas you will need
to solve problems involving forced vibrations.



 Solution
for Rotor Excitation
Solution
for Rotor Excitation
![]() The
steady state response is always harmonic, and has the same frequency as that of
the forcing.
The
steady state response is always harmonic, and has the same frequency as that of
the forcing.![]() The amplitude of vibration is
strongly dependent on the frequency of excitation, and on the properties of the
springmass system.
The amplitude of vibration is
strongly dependent on the frequency of excitation, and on the properties of the
springmass system.![]() If the forcing
frequency is close to the natural frequency of the system, and the system is
lightly damped, huge vibration amplitudes may occur. This phenomenon is known as resonance.
If the forcing
frequency is close to the natural frequency of the system, and the system is
lightly damped, huge vibration amplitudes may occur. This phenomenon is known as resonance. ![]() There is a phase lag between the
forcing and the system response, which depends on the frequency of excitation
and the properties of the spring-mass system.
There is a phase lag between the
forcing and the system response, which depends on the frequency of excitation
and the properties of the spring-mass system. Preventing a
system from vibrating: Suppose that
we need to stop a structure or component from vibrating e.g. to stop a tall building from
swaying. Structures are always
deformable to some extent this is represented qualitatively by the
spring in a spring-mass system. They
always have mass this is represented by the mass of the
block. Finally, the damper represents
energy dissipation. Forces acting on a
system generally fluctuate with time.
They probably aren’t perfectly harmonic, but they usually do have a
fairly well defined frequency (visualize waves on the ocean, for example, or
wind gusts. Many vibrations are
man-made, in which case their frequency is known for example vehicles traveling on a road tend
to induce vibrations with a frequency of about 2Hz, corresponding to the bounce
of the car on its suspension).
Preventing a
system from vibrating: Suppose that
we need to stop a structure or component from vibrating e.g. to stop a tall building from
swaying. Structures are always
deformable to some extent this is represented qualitatively by the
spring in a spring-mass system. They
always have mass this is represented by the mass of the
block. Finally, the damper represents
energy dissipation. Forces acting on a
system generally fluctuate with time.
They probably aren’t perfectly harmonic, but they usually do have a
fairly well defined frequency (visualize waves on the ocean, for example, or
wind gusts. Many vibrations are
man-made, in which case their frequency is known for example vehicles traveling on a road tend
to induce vibrations with a frequency of about 2Hz, corresponding to the bounce
of the car on its suspension).
 Designing a suspension or vibration isolation system. Suspensions, and vibration isolation systems,
are examples of base excited systems. In
this case, the system really consists of a mass (the vehicle, or the isolation
table) on a spring (the shock absorber or vibration isolation pad). We expect that the base will vibrate with some
characteristic frequency .
Our goal is to design the system to minimize the vibration of the mass.
Designing a suspension or vibration isolation system. Suspensions, and vibration isolation systems,
are examples of base excited systems. In
this case, the system really consists of a mass (the vehicle, or the isolation
table) on a spring (the shock absorber or vibration isolation pad). We expect that the base will vibrate with some
characteristic frequency .
Our goal is to design the system to minimize the vibration of the mass.
 5.4.7 Example Problems in Forced Vibrations
5.4.7 Example Problems in Forced Vibrations

![]() Define
Define ![]() Any complex number z can be split into imaginary and real parts as
Any complex number z can be split into imaginary and real parts as![]() Define the complex conjugate as
Define the complex conjugate as ![]() It follows that
It follows that ![]() The exponential of an imaginary number
(Euler’s formula) is
The exponential of an imaginary number
(Euler’s formula) is![]() Euler’s formula enables us to write any
complex number in polar form
Euler’s formula enables us to write any
complex number in polar form![]() Euler’s formula also allows us to represent
trig functions as complex exponentials
Euler’s formula also allows us to represent
trig functions as complex exponentials![]() Note that
Note that  We always express the equations of motion for a system
with many degrees of freedom in a standard form. The two degree of freedom system shown in the
picture can be used as an example. We
won’t go through the calculation in detail here (you should be able to derive
it for yourself draw a FBD, use Newton’s law and all that
tedious stuff), but here is the final answer:
We always express the equations of motion for a system
with many degrees of freedom in a standard form. The two degree of freedom system shown in the
picture can be used as an example. We
won’t go through the calculation in detail here (you should be able to derive
it for yourself draw a FBD, use Newton’s law and all that
tedious stuff), but here is the final answer: The spring-mass system is linear. A nonlinear system has more complicated
equations of motion, but these can always be arranged into the standard matrix
form by assuming that the displacement of the system is small, and linearizing
the equation of motion. For example, the
full nonlinear equations of motion for the double pendulum shown in the figure
are
The spring-mass system is linear. A nonlinear system has more complicated
equations of motion, but these can always be arranged into the standard matrix
form by assuming that the displacement of the system is small, and linearizing
the equation of motion. For example, the
full nonlinear equations of motion for the double pendulum shown in the figure
are



![]()
![]() ,
, ![]() , where
, where ![]() are the (unknown)
amplitudes of vibration of the two masses.
In vector form we could write
are the (unknown)
amplitudes of vibration of the two masses.
In vector form we could write ![]() , where
, where ![]() . Substituting this
into the equation of motion gives
. Substituting this
into the equation of motion gives 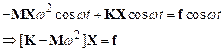
![]() , and the springs all have the same stiffness
, and the springs all have the same stiffness ![]() . The first mass is
subjected to a harmonic force
. The first mass is
subjected to a harmonic force ![]() , and no force acts on the second mass. Note that the graph shows the magnitude of
the vibration amplitude the formula predicts that for some frequencies
some masses have negative vibration amplitudes, but the negative sign has been
ignored, as the negative sign just means that the mass vibrates out of phase
with the force.
, and no force acts on the second mass. Note that the graph shows the magnitude of
the vibration amplitude the formula predicts that for some frequencies
some masses have negative vibration amplitudes, but the negative sign has been
ignored, as the negative sign just means that the mass vibrates out of phase
with the force.
![]()
 If the forcing frequency is close to
any one of the natural frequencies of the system, huge vibration amplitudes
occur. This phenomenon is known as resonance. You can check the natural frequencies of the
system using the little matlab code in section 5.5.2 they turn out to be
If the forcing frequency is close to
any one of the natural frequencies of the system, huge vibration amplitudes
occur. This phenomenon is known as resonance. You can check the natural frequencies of the
system using the little matlab code in section 5.5.2 they turn out to be ![]() and
and ![]() . At these frequencies
the vibration amplitude is theoretically infinite.
. At these frequencies
the vibration amplitude is theoretically infinite.![]() The figure predicts an intriguing new
phenomenon at a magic frequency, the amplitude of
vibration of mass 1 (that’s the mass that the force acts on) drops to
zero. This is called ‘Anti-resonance,’
and it has an important engineering application. Suppose that we have designed a system with a
serious vibration problem (like the London Millenium bridge). Usually, this occurs because some kind of
unexpected force is exciting one of the vibration modes in the system. We can idealize this behavior as a
mass-spring system subjected to a force, as shown in the figure. So how do we stop the system from
vibrating? Our solution for a 2DOF
system shows that a system with two masses will have an anti-resonance. So we simply turn our 1DOF system into a 2DOF
system by adding another spring and a mass, and tune the stiffness and mass of
the new elements so that the anti-resonance occurs at the appropriate
frequency. Of course, adding a mass
will create a new vibration mode, but we can make sure that the new natural
frequency is not at a bad frequency. We
can also add a dashpot in parallel with the spring, if we want this has the effect of making the
anti-resonance phenomenon somewhat less effective (the vibration amplitude will
be small, but finite, at the ‘magic’ frequency), but the new vibration modes
will also have lower amplitudes at resonance. The added spring mass system is called a ‘tuned vibration
absorber.’ This approach was used to solve the Millenium Bridge
vibration problem.
The figure predicts an intriguing new
phenomenon at a magic frequency, the amplitude of
vibration of mass 1 (that’s the mass that the force acts on) drops to
zero. This is called ‘Anti-resonance,’
and it has an important engineering application. Suppose that we have designed a system with a
serious vibration problem (like the London Millenium bridge). Usually, this occurs because some kind of
unexpected force is exciting one of the vibration modes in the system. We can idealize this behavior as a
mass-spring system subjected to a force, as shown in the figure. So how do we stop the system from
vibrating? Our solution for a 2DOF
system shows that a system with two masses will have an anti-resonance. So we simply turn our 1DOF system into a 2DOF
system by adding another spring and a mass, and tune the stiffness and mass of
the new elements so that the anti-resonance occurs at the appropriate
frequency. Of course, adding a mass
will create a new vibration mode, but we can make sure that the new natural
frequency is not at a bad frequency. We
can also add a dashpot in parallel with the spring, if we want this has the effect of making the
anti-resonance phenomenon somewhat less effective (the vibration amplitude will
be small, but finite, at the ‘magic’ frequency), but the new vibration modes
will also have lower amplitudes at resonance. The added spring mass system is called a ‘tuned vibration
absorber.’ This approach was used to solve the Millenium Bridge
vibration problem. In most design calculations, we don’t worry about
accounting for the effects of damping very accurately. This is partly because it’s very difficult to
find formulas that model damping realistically, and even more difficult to find
values for the damping parameters.
Also, the mathematics required to solve damped problems is a bit messy.
Old textbooks don’t cover it, because for practical purposes it is only
possible to do the calculations using a computer. It is not hard to account for the effects of
damping, however, and it is helpful to have a sense of what its effect will be
in a real system. We’ll go through this
rather briefly in this section.
In most design calculations, we don’t worry about
accounting for the effects of damping very accurately. This is partly because it’s very difficult to
find formulas that model damping realistically, and even more difficult to find
values for the damping parameters.
Also, the mathematics required to solve damped problems is a bit messy.
Old textbooks don’t cover it, because for practical purposes it is only
possible to do the calculations using a computer. It is not hard to account for the effects of
damping, however, and it is helpful to have a sense of what its effect will be
in a real system. We’ll go through this
rather briefly in this section.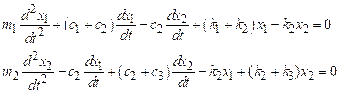
![]() and
and ![]()
![]() as new variables, and
then write the equations in matrix form as
as new variables, and
then write the equations in matrix form as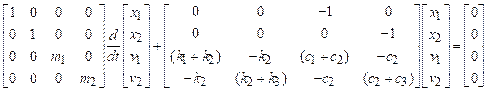
![]()
![]() , and we wish to calculate the subsequent motion of the
system. To do this, we must solve the equation of motion. We start by guessing
that the solution has the form
, and we wish to calculate the subsequent motion of the
system. To do this, we must solve the equation of motion. We start by guessing
that the solution has the form ![]() (the negative sign is
introduced because we expect solutions to decay with time). Here,
(the negative sign is
introduced because we expect solutions to decay with time). Here, ![]() is a constant vector,
to be determined. Substituting this
into the equation of motion gives
is a constant vector,
to be determined. Substituting this
into the equation of motion gives![]()
![]() and
and ![]() that satisfy the
equation are in general complex that is to say, each
that satisfy the
equation are in general complex that is to say, each ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are positive real numbers, and
are positive real numbers, and ![]() . This makes more
sense if we recall Euler’s formula
. This makes more
sense if we recall Euler’s formula ![]()
![]() and
and ![]() have been calculated,
the response of the system can be calculated as follows:
have been calculated,
the response of the system can be calculated as follows:![]() (MATLAB constructs
this matrix automatically)
(MATLAB constructs
this matrix automatically)![]() (t), which has the form
(t), which has the form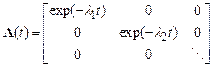
![]() is one of the
solutions to the generalized eigenvalue equation.
is one of the
solutions to the generalized eigenvalue equation.![]()
![]()
 HEALTH
WARNING: The formulas listed here
only work if all the generalized eigenvalues
HEALTH
WARNING: The formulas listed here
only work if all the generalized eigenvalues ![]() satisfying
satisfying ![]() are different. For
some very special choices of damping, some eigenvalues may be repeated. In this case the formula won’t work. A quick and dirty fix for this is just to
change the damping very slightly, and the problem disappears. Your applied math courses will hopefully
show you a better fix, but we won’t worry about that here.
are different. For
some very special choices of damping, some eigenvalues may be repeated. In this case the formula won’t work. A quick and dirty fix for this is just to
change the damping very slightly, and the problem disappears. Your applied math courses will hopefully
show you a better fix, but we won’t worry about that here. ![]() . In each case, the graph plots the motion of the three
masses if a color doesn’t show up, it means one of
the other masses has the exact same displacement.
. In each case, the graph plots the motion of the three
masses if a color doesn’t show up, it means one of
the other masses has the exact same displacement.


 This explains why it is so helpful to understand the
behavior of a 1DOF system. If a more
complicated system is set in motion, its response initially involves
contributions from all its vibration modes.
Soon, however, the high frequency modes die out, and the dominant
behavior is just caused by the lowest frequency mode. The animation to the
right demonstrates this very nicely here, the system was started by displacing
only the first mass. The initial
response is not harmonic, but after a short time the high frequency modes stop
contributing, and the system behaves just like a 1DOF approximation. For design purposes, idealizing the system as
a 1DOF damped spring-mass system is usually sufficient.
This explains why it is so helpful to understand the
behavior of a 1DOF system. If a more
complicated system is set in motion, its response initially involves
contributions from all its vibration modes.
Soon, however, the high frequency modes die out, and the dominant
behavior is just caused by the lowest frequency mode. The animation to the
right demonstrates this very nicely here, the system was started by displacing
only the first mass. The initial
response is not harmonic, but after a short time the high frequency modes stop
contributing, and the system behaves just like a 1DOF approximation. For design purposes, idealizing the system as
a 1DOF damped spring-mass system is usually sufficient.![]() or higher. Systems of this kind are not of much
practical interest.
or higher. Systems of this kind are not of much
practical interest.
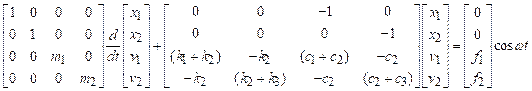
![]()
![]()
![]() , and substituting into the matrix equation
, and substituting into the matrix equation![]()
![]() . Similarly, we can
solve
. Similarly, we can
solve![]()
![]() , which gives an equation for
, which gives an equation for ![]() of the form
of the form ![]() . You actually don’t need to solve this equation you can simply calculate
. You actually don’t need to solve this equation you can simply calculate ![]() by just changing the
sign of all the imaginary parts of
by just changing the
sign of all the imaginary parts of ![]() . The full solution follows as
. The full solution follows as![]()
![]() ,
, ![]() denote the components
of
denote the components
of ![]() and
and ![]()
![]()
![]()